Equalize BSPK Signal
Equalize a BPSK signal using a linear equalizer with a least mean square (LMS) algorithm.
Generate random binary data and apply BPSK modulation.
M = 2; data = randi([0 1],1000,1); modData = pskmod(data,M);
Apply two-tap static fading to the modulated signal and add AWGN noise.
rxSig = conv(modData,[0.02+0.5i 0.05]); rxSig = awgn(rxSig,30);
Create a linear equalizer System object™ configured to use the LMS adaptive algorithm, 8 taps, 0.1 step size, and the 4th tap as the reference tap. Set the constellation to match the modulation of the transmitted signal.
lineq = comm.LinearEqualizer( ... NumTaps=8, ... StepSize=0.1, ... Constellation=complex([-1 1]), ... ReferenceTap=4)
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'LMS'
NumTaps: 8
StepSize: 0.1000
Constellation: [-1.0000 + 0.0000i 1.0000 + 0.0000i]
ReferenceTap: 4
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
Equalize the received signal, rxSig. Use the first 200 data bits as a training sequence. Display a constellation diagram showing the received signal before and after equalization.
trSeq = modData(1:200); [eqSig,err] = lineq(rxSig,trSeq); constdiag = comm.ConstellationDiagram( ... NumInputPorts=2, ... ChannelNames={'Before equalization','After equalization'}, ... ReferenceConstellation=pskmod([0 M-1],M)); constdiag(rxSig(400:end),eqSig(400:end))
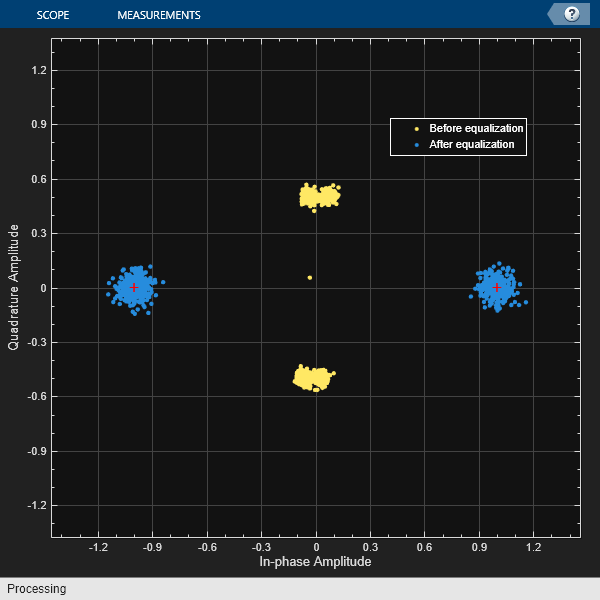
Plot the magnitude of the error estimate. As shown by the decrease and stabilizing of the error signal, the equalization converges in less than 200 bits.
plot(abs(err)) title('Error Estimate') xlabel('Bits') ylabel('Amplitude (V)')
