Anomaly Detection in Industrial Machinery Using Three-Axis Vibration Data
This example shows how to detect anomalies in vibration data using machine learning and deep learning. The example uses vibration data from an industrial machine. First, you extract features from the raw measurements corresponding to normal operation using the Diagnostic Feature Designer App. You use the selected features to train three different models (one-class SVM, isolation forest, and LSTM autoencoder) for anomaly detection. Then, you use each trained model to identify whether the machine is operating normally.
Data Set
The data set contains three-axis vibration measurements from an industrial machine. The data is collected both immediately before and after a scheduled maintenance. The data collected after scheduled maintenance is assumed to represent normal operating conditions of the machine. The data from before maintenance can represent either normal or anomalous conditions. Data for each axis is stored in a separate column. Save and unzip the data set and then, load the training data.
url = 'https://ssd.mathworks.com/supportfiles/predmaint/anomalyDetection3axisVibration/v1/vibrationData.zip'; websave('vibrationData.zip',url); unzip('vibrationData.zip'); load("MachineData.mat") trainData
trainData=40×4 table
ch1 ch2 ch3 label
________________ ________________ ________________ ______
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
⋮
To better understand the data, visualize it before and after maintenance. Plot vibration data for the fourth member of the ensemble and note that the data for the two conditions looks different.
ensMember = 4; helperPlotVibrationData(trainData, ensMember)
Extract Features with Diagnostic Feature Designer App
Because raw data can be correlated and noisy, using raw data for training machine learning models is not very efficient. The Diagnostic Feature Designer (Predictive Maintenance Toolbox) app lets you interactively explore and preprocess your data, extract time and frequency domain features, and then rank the features to determine which are most effective for diagnosing faulty or otherwise anomalous systems. You can then export a function to extract the selected features from your data set programmatically. Open Diagnostic Feature Designer by typing diagnosticFeatureDesigner at the command prompt. For a tutorial on using Diagnostic Feature Designer, see Design Condition Indicators for Predictive Maintenance Algorithms (Predictive Maintenance Toolbox).
Click the New Session button, select trainData as the source, and then set label as Condition Variable. The label variable identifies the condition of the machine for the corresponding data.
You can use Diagnostic Feature Designer to iterate on the features and rank them. The app creates a histogram view for all generated features to visualize the distribution for each label. For example, the following histograms show distributions of various features extracted from ch1. These histograms are derived from a much larger data set than the data set that you use in this example, in order to better illustrate the label-group separation. Because you are using a smaller data set, your results will look different.
Use the top four ranked features for each channel.
ch1 : Crest Factor, Kurtosis, RMS, Std
ch2 : Mean, RMS, Skewness, Std
ch3 : Crest Factor, SINAD, SNR, THD
Export a function to generate the features from the Diagnostic Feature designer app and save it with the name generateFeatures. This function extracts the top 4 relevant features from each channel in the entire data set from the command line.
trainFeatures = generateFeatures(trainData); head(trainFeatures)
label ch1_stats/Col1_CrestFactor ch1_stats/Col1_Kurtosis ch1_stats/Col1_RMS ch1_stats/Col1_Std ch2_stats/Col1_Mean ch2_stats/Col1_RMS ch2_stats/Col1_Skewness ch2_stats/Col1_Std ch3_stats/Col1_CrestFactor ch3_stats/Col1_SINAD ch3_stats/Col1_SNR ch3_stats/Col1_THD
______ __________________________ _______________________ __________________ __________________ ___________________ __________________ _______________________ __________________ __________________________ ____________________ __________________ __________________
Before 2.2811 1.8087 2.3074 2.3071 -0.032332 0.64962 4.523 0.64882 11.973 -15.945 -15.886 -2.732
Before 2.3276 1.8379 2.2613 2.261 -0.03331 0.59458 5.548 0.59365 10.284 -15.984 -15.927 -2.7507
Before 2.3276 1.8626 2.2613 2.2612 -0.012052 0.48248 4.3638 0.48233 8.9125 -15.858 -15.798 -2.7104
Before 2.8781 2.1986 1.8288 1.8285 -0.005049 0.34984 2.3324 0.34981 11.795 -16.191 -16.14 -3.0683
Before 2.8911 2.06 1.8205 1.8203 -0.0018988 0.27366 1.7661 0.27365 11.395 -15.947 -15.893 -3.1126
Before 2.8979 2.1204 1.8163 1.8162 -0.0044174 0.3674 2.8969 0.36737 11.685 -15.963 -15.908 -2.9761
Before 2.9494 1.92 1.7846 1.7844 -0.0067284 0.36262 4.1308 0.36256 12.396 -15.999 -15.942 -2.8281
Before 2.5106 1.6774 1.7513 1.7511 -0.0089548 0.32348 3.7691 0.32335 8.8808 -15.79 -15.732 -2.9532
Prepare Full Data Sets for Training
The data set you use to this point is only a small subset of a much larger data set to illustrate the process of feature extraction and selection. Training your algorithm on all available data yields the best performance. To this end, load the same 12 features as previously extracted from the larger data set of 17,642 signals.
load("FeatureEntire.mat")
head(featureAll) label ch1_stats/Col1_CrestFactor ch1_stats/Col1_Kurtosis ch1_stats/Col1_RMS ch1_stats/Col1_Std ch2_stats/Col1_Mean ch2_stats/Col1_RMS ch2_stats/Col1_Skewness ch2_stats/Col1_Std ch3_stats/Col1_CrestFactor ch3_stats/Col1_SINAD ch3_stats/Col1_SNR ch3_stats/Col1_THD
______ __________________________ _______________________ __________________ __________________ ___________________ __________________ _______________________ __________________ __________________________ ____________________ __________________ __________________
Before 2.3683 1.927 2.2225 2.2225 -0.015149 0.62512 4.2931 0.62495 5.6569 -5.4476 -4.9977 -4.4608
Before 2.402 1.9206 2.1807 2.1803 -0.018269 0.56773 3.9985 0.56744 8.7481 -12.532 -12.419 -3.2353
Before 2.4157 1.9523 2.1789 2.1788 -0.0063652 0.45646 2.8886 0.45642 8.3111 -12.977 -12.869 -2.9591
Before 2.4595 1.8205 2.14 2.1401 0.0017307 0.41418 2.0635 0.41418 7.2318 -13.566 -13.468 -2.7944
Before 2.2502 1.8609 2.3391 2.339 -0.0081829 0.3694 3.3498 0.36931 6.8134 -13.33 -13.225 -2.7182
Before 2.4211 2.2479 2.1286 2.1285 0.011139 0.36638 1.8602 0.36621 7.4712 -13.324 -13.226 -3.0313
Before 3.3111 4.0304 1.5896 1.5896 -0.0080759 0.47218 2.1132 0.47211 8.2412 -13.85 -13.758 -2.7822
Before 2.2655 2.0656 2.3233 2.3233 -0.0049447 0.37829 2.4936 0.37827 7.6947 -13.781 -13.683 -2.5601
Use cvpartition to partition data into a training set and an independent test set. Use the helperExtractLabeledData helper function to find all features corresponding to the label 'After' in the featureTrain variable.
rng(0) % set for reproducibility idx = cvpartition(featureAll.label, 'holdout', 0.1); featureTrain = featureAll(idx.training, :); featureTest = featureAll(idx.test, :);
For each model, train on only the after maintenance data, which is assumed to be normal. Extract only this data from featureTrain.
trueAnomaliesTest = featureTest.label;
featureNormal = featureTrain(featureTrain.label=='After', :);Detect Anomalies with One-Class SVM
Support Vector Machines are powerful classifiers, and the variant that trains on only the normal data is used here.. This model works well for identifying abnormalities that are "far" from the normal data. Train a one-class SVM model using the fitcsvm function and the data for normal conditions.
mdlSVM = fitcsvm(featureNormal, 'label', 'Standardize', true, 'OutlierFraction', 0);
Validate the trained SVM model by using test data, which contains both normal and anomalous data.
featureTestNoLabels = featureTest(:, 2:end); [~,scoreSVM] = predict(mdlSVM,featureTestNoLabels); isanomalySVM = scoreSVM<0; predSVM = categorical(isanomalySVM, [1, 0], ["Anomaly", "Normal"]); trueAnomaliesTest = renamecats(trueAnomaliesTest,["After","Before"], ["Normal","Anomaly"]); figure; confusionchart(trueAnomaliesTest, predSVM, Title="Anomaly Detection with One-class SVM", Normalization="row-normalized");
From the confusion matrix, you can see that the one-class SVM performs well. Only 0.3% of anomalous samples are misclassified as normal and about 0.9% of normal data is misclassified as anomalous.
Detect Anomalies with Isolation Forest
The decision trees of an isolation forest isolate each observation in a leaf. How many decisions a sample passes through to get to its leaf is a measure of how difficult isolating it from the others is. The average depth of trees for a specific sample is used as their anomaly score and returned by iforest.
Train the isolation forest model on normal data only.
[mdlIF,~,scoreTrainIF] = iforest(featureNormal{:,2:13},'ContaminationFraction',0.09);Validate the trained isolation forest model by using the test data. Visualize the performance of this model by using a confusion chart.
[isanomalyIF,scoreTestIF] = isanomaly(mdlIF,featureTestNoLabels.Variables); predIF = categorical(isanomalyIF, [1, 0], ["Anomaly", "Normal"]); figure; confusionchart(trueAnomaliesTest,predIF,Title="Anomaly Detection with Isolation Forest",Normalization="row-normalized");
On this data, the isolation forest doesn't do as well as the one-class SVM. The reason for this poorer performance is that the training data contains only normal data while the test data contains about 30% anomalous data. Therefore, the isolation forest model is a better choice when the proportion of anomalous data to normal data is similar for both training and test data.
Detect Anomalies with LSTM Autoencoder Network
Autoencoders are a type of neural network that learn a compressed representation of unlabeled data. LSTM autoencoders are a variant of this network that can learn a compressed representation of sequence data. Here, you train an LSTM autoencoder with only normal data and use this trained network to identify when a signal does not look normal.
Start by extracting features from the after maintenance data.
featuresAfter = helperExtractLabeledData(featureTrain, ... "After");
Construct the LSTM autoencoder network and set the training options.
featureDimension = 1; % Define biLSTM network layers layers = [ sequenceInputLayer(featureDimension) bilstmLayer(16) reluLayer bilstmLayer(32) reluLayer bilstmLayer(16) reluLayer fullyConnectedLayer(featureDimension)]; % Set Training Options options = trainingOptions('adam', ... 'Plots', 'training-progress', ... 'Metrics', 'rmse', ... 'MiniBatchSize', 500,... 'MaxEpochs',200);
The MaxEpochs training options parameter is set to 200. For higher validation accuracy, you can set this parameter to a larger number; However, the network might overfit.
Train the model using trainnet and specify mean-squared-error (mse) as the loss function.
net = trainnet(featuresAfter, featuresAfter, layers, "mse", options); Iteration Epoch TimeElapsed LearnRate TrainingLoss TrainingRMSE
_________ _____ ___________ _________ ____________ ____________
1 1 00:00:09 0.001 33.771 5.8113
50 3 00:00:15 0.001 29.543 5.4353
100 5 00:00:19 0.001 15.904 3.988
150 8 00:00:24 0.001 18.274 4.2748
200 10 00:00:29 0.001 12.052 3.4716
250 13 00:00:33 0.001 15.794 3.9742
300 15 00:00:38 0.001 10.051 3.1703
350 18 00:00:42 0.001 13.84 3.7202
400 20 00:00:47 0.001 8.359 2.8912
450 23 00:00:51 0.001 12.185 3.4907
500 25 00:00:55 0.001 7.1721 2.6781
550 28 00:01:00 0.001 11.018 3.3194
600 30 00:01:04 0.001 6.2384 2.4977
650 33 00:01:08 0.001 10.009 3.1637
700 35 00:01:12 0.001 5.3576 2.3146
750 38 00:01:16 0.001 8.8568 2.976
800 40 00:01:20 0.001 4.5712 2.138
850 43 00:01:24 0.001 8.0863 2.8436
900 45 00:01:28 0.001 4.0192 2.0048
950 48 00:01:32 0.001 7.456 2.7306
1000 50 00:01:36 0.001 3.6334 1.9061
1050 53 00:01:41 0.001 6.9985 2.6455
1100 55 00:01:45 0.001 3.332 1.8254
1150 58 00:01:49 0.001 6.5709 2.5634
1200 60 00:01:53 0.001 3.0456 1.7452
1250 63 00:01:57 0.001 6.2219 2.4944
1300 65 00:02:00 0.001 2.8124 1.677
1350 68 00:02:04 0.001 5.868 2.4224
1400 70 00:02:08 0.001 2.4919 1.5786
1450 73 00:02:12 0.001 5.3488 2.3127
1500 75 00:02:16 0.001 2.161 1.47
1550 78 00:02:20 0.001 4.9866 2.2331
1600 80 00:02:24 0.001 1.9088 1.3816
1650 83 00:02:28 0.001 4.6791 2.1631
1700 85 00:02:32 0.001 1.7001 1.3039
1750 88 00:02:36 0.001 4.4113 2.1003
1800 90 00:02:41 0.001 1.5254 1.2351
1850 93 00:02:45 0.001 4.1853 2.0458
1900 95 00:02:49 0.001 1.3738 1.1721
1950 98 00:02:53 0.001 3.9576 1.9894
2000 100 00:02:57 0.001 1.2387 1.113
2050 103 00:03:01 0.001 3.7698 1.9416
2100 105 00:03:05 0.001 1.123 1.0597
2150 108 00:03:09 0.001 3.6016 1.8978
2200 110 00:03:13 0.001 1.0263 1.0131
2250 113 00:03:17 0.001 3.4534 1.8583
2300 115 00:03:21 0.001 0.94179 0.97046
2350 118 00:03:25 0.001 3.3239 1.8232
2400 120 00:03:29 0.001 0.87847 0.93727
2450 123 00:03:34 0.001 3.2066 1.7907
2500 125 00:03:38 0.001 0.80876 0.89931
2550 128 00:03:42 0.001 3.0997 1.7606
2600 130 00:03:46 0.001 0.74998 0.86601
2650 133 00:03:50 0.001 3.0022 1.7327
2700 135 00:03:54 0.001 0.70011 0.83672
2750 138 00:03:58 0.001 2.9062 1.7047
2800 140 00:04:02 0.001 0.6546 0.80908
2850 143 00:04:05 0.001 2.8237 1.6804
2900 145 00:04:09 0.001 0.6157 0.78466
2950 148 00:04:13 0.001 2.7403 1.6554
3000 150 00:04:18 0.001 0.5843 0.7644
3050 153 00:04:22 0.001 2.665 1.6325
3100 155 00:04:25 0.001 0.54377 0.73741
3150 158 00:04:29 0.001 2.5921 1.61
3200 160 00:04:33 0.001 0.51321 0.71639
3250 163 00:04:37 0.001 2.5235 1.5886
3300 165 00:04:41 0.001 0.49071 0.70051
3350 168 00:04:45 0.001 2.4591 1.5682
3400 170 00:04:49 0.001 0.46161 0.67942
3450 173 00:04:53 0.001 2.3967 1.5481
3500 175 00:04:57 0.001 0.43363 0.65851
3550 178 00:05:01 0.001 2.3392 1.5295
3600 180 00:05:05 0.001 0.41236 0.64215
3650 183 00:05:09 0.001 2.2851 1.5116
3700 185 00:05:13 0.001 0.39331 0.62715
3750 188 00:05:17 0.001 2.234 1.4947
3800 190 00:05:21 0.001 0.37487 0.61227
3850 193 00:05:24 0.001 2.1853 1.4783
3900 195 00:05:28 0.001 0.35768 0.59806
3950 198 00:05:32 0.001 2.1387 1.4624
4000 200 00:05:36 0.001 0.34181 0.58465
Training stopped: Max epochs completed
Visualize Model Behavior and Error on Validation Data
Extract and visualize a sample each from Anomalous and Normal condition. The following plots show the reconstruction errors of the autoencoder model for each of the 12 features (indicated on the X-axis). The reconstructed feature value is referred to as "Decoded" signal in the plot. In this sample, features 10, 11, and 12 do not reconstruct well for the anomalous input and thus have high errors. We can use reconstructon errors to identify an anomaly.
testNormal = featureTest(1200, 2:end).Variables'; testAnomaly = featureTest(200, 2:end).Variables'; % Predict decoded signal for both decodedNormal = predict(net,testNormal); decodedAnomaly = predict(net,testAnomaly); % Visualize helperVisualizeModelBehavior(testNormal, testAnomaly, decodedNormal, decodedAnomaly)
Extract features for all the normal and anomalous data. Use the trained autoencoder model to predict the selected 12 features for both before and after maintenance data. The following plots show the root mean square reconstruction error across the twelve features. The figure shows that the reconstruction error for the anomalous data is much higher than the normal data. This result is expected, since the autoencoder is trained on the normal data, so it better reconstructs similar signals.
% Extract data Before maintenance XTestBefore = helperExtractLabeledData(featureTest, "Before"); % Predict output before maintenance and calculate error yHatBefore = minibatchpredict(net, XTestBefore, 'UniformOutput', false); errorBefore = helperCalculateError(XTestBefore, yHatBefore); % Extract data after maintenance XTestAfter = helperExtractLabeledData(featureTest, "After"); % Predict output after maintenance and calculate error yHatAfter = minibatchpredict(net, XTestAfter, 'UniformOutput', false); errorAfter = helperCalculateError(XTestAfter, yHatAfter); helperVisualizeError(errorBefore, errorAfter);
Identify Anomalies
Calculate the reconstruction error on the full validation data.
XTestAll = helperExtractLabeledData(featureTest, "All"); yHatAll = minibatchpredict(net, XTestAll, 'UniformOutput', false); errorAll = helperCalculateError(XTestAll, yHatAll);
Define an anomaly as a point that has reconstruction error 0.5 times the mean across all observations. This threshold was determined through previous experimentation and can be changed as required.
thresh = 0.5; anomalies = errorAll > thresh*mean(errorAll); helperVisualizeAnomalies(anomalies, errorAll, featureTest);
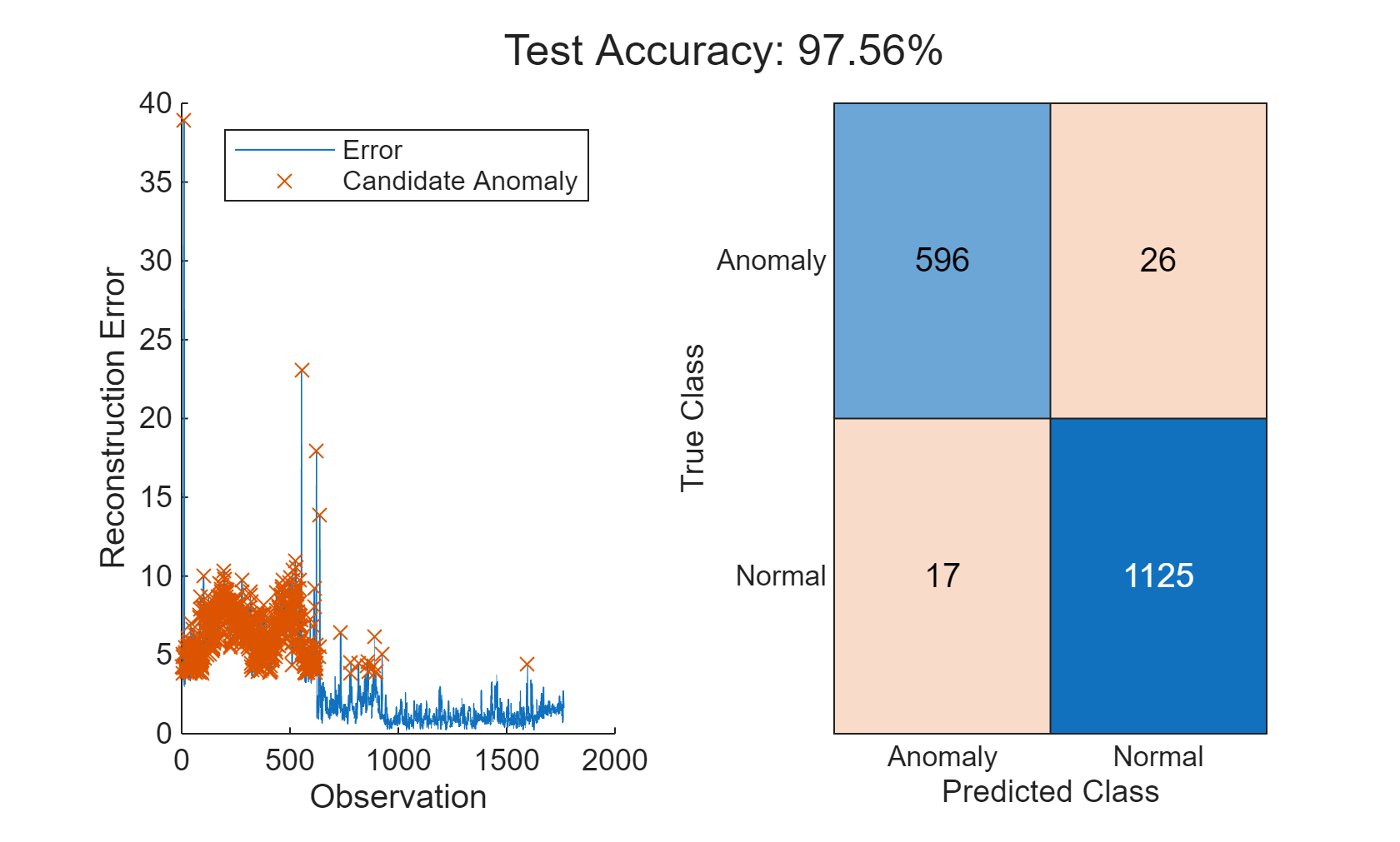
In this example, three different models are used to detect anomalies. The one-class SVM had the best performance at 99.7% for detecting anomalies in the test data, while the other two models are around 93% accurate. The relative performance of the models can change if a different set of features are selected or if different hyper-parameters are used for each model. Use the Diagnostic Feature Designer MATLAB App to further experiment with feature selection.
Supporting Functions
function E = helperCalculateError(X, Y) % HELPERCALCULATEERROR calculates the rms error value between the % inputs X, Y E = zeros(length(X),1); for i = 1:length(X) E(i,:) = sqrt(sum((Y{i} - X{i}).^2)); end end function helperVisualizeError(errorBefore, errorAfter) % HELPERVISUALIZEERROR creates a plot to visualize the errors on detecting % before and after conditions figure("Color", "W") tiledlayout("flow") nexttile plot(1:length(errorBefore), errorBefore, 'LineWidth',1.5), grid on title(["Before Maintenance", ... sprintf("Mean Error: %.2f\n", mean(errorBefore))]) xlabel("Observations") ylabel("Reconstruction Error") ylim([0 15]) nexttile plot(1:length(errorAfter), errorAfter, 'LineWidth',1.5), grid on, title(["After Maintenance", ... sprintf("Mean Error: %.2f\n", mean(errorAfter))]) xlabel("Observations") ylabel("Reconstruction Error") ylim([0 15]) end function helperVisualizeAnomalies(anomalies, errorAll, featureTest) % HELPERVISUALIZEANOMALIES creates a plot of the detected anomalies anomalyIdx = find(anomalies); anomalyErr = errorAll(anomalies); predAE = categorical(anomalies, [1, 0], ["Anomaly", "Normal"]); trueAE = renamecats(featureTest.label,["Before","After"],["Anomaly","Normal"]); acc = numel(find(trueAE == predAE))/numel(predAE)*100; figure; t = tiledlayout("flow"); title(t, "Test Accuracy: " + round(mean(acc),2) + "%"); nexttile hold on plot(errorAll) plot(anomalyIdx, anomalyErr, 'x') hold off ylabel("Reconstruction Error") xlabel("Observation") legend("Error", "Candidate Anomaly") nexttile confusionchart(trueAE,predAE) end function helperVisualizeModelBehavior(normalData, abnormalData, decodedNorm, decodedAbNorm) %HELPERVISUALIZEMODELBEHAVIOR Visualize model behavior on sample validation data figure("Color", "W") tiledlayout("flow") nexttile() hold on colororder('default') yyaxis left plot(normalData') plot(decodedNorm',":","LineWidth",1.5) hold off title("Normal Input") grid on ylabel("Feature Value") yyaxis right stem(abs(normalData' - decodedNorm')) ylim([0 2]) ylabel("Error") legend(["Input", "Decoded","Error"],"Location","southwest") nexttile() hold on yyaxis left plot(abnormalData) plot(decodedAbNorm',":","LineWidth",1.5) hold off title("Abnormal Input") grid on ylabel("Feature Value") yyaxis right stem(abs(abnormalData' - decodedAbNorm')) ylim([0 2]) ylabel("Error") legend(["Input", "Decoded","Error"],"Location","southwest") end function X = helperExtractLabeledData(featureTable, label) %HELPEREXTRACTLABELEDDATA Extract data from before or after operating %conditions and re-format to support input to autoencoder network % Select data with label After if label == "All" Xtemp = featureTable(:, 2:end).Variables; else tF = featureTable.label == label; Xtemp = featureTable(tF, 2:end).Variables; end % Arrange data into cells X = cell(length(Xtemp),1); for i = 1:length(Xtemp) X{i,:} = Xtemp(i,:)'; end end
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)