Esta página se ha traducido mediante traducción automática. Haga clic aquí para ver la última versión en inglés.

Minimizar la función de Rastrigins usando ga, basado en problemas

Este ejemplo muestra cómo minimizar una función con múltiples mínimos utilizando el algoritmo genético en el enfoque basado en problemas. Para dos variables x y y, la función de Rastrigin se define de la siguiente manera.

ras = @(x, y) 20 + x.^2 + y.^2 - 10*(cos(2*pi*x) + cos(2*pi*y));

Grafique la función escalada por 10 en cada dirección.

rf3 = @(x, y) ras(x/10, y/10);
fsurf(rf3,[-30 30],"ShowContours","on")
title("rastriginsfcn([x/10,y/10])")
xlabel("x")
ylabel("y")

La función tiene muchos mínimos locales y un valor mínimo global de 0 que se alcanza en x = 0, y = 0. Ver ¿Qué es la optimización global?

Crear variables de optimización x y y. Especifica que las variables están delimitadas por $$\pm 100$$.

x = optimvar("x","LowerBound",-100,"UpperBound",100);
y = optimvar("y","LowerBound",-100,"UpperBound",100);

Cree un problema de optimización con la función objetivo rastriginsfcn(x).

prob = optimproblem("Objective",ras(x,y));

Nota: Si tiene una función no lineal que no está compuesta por polinomios, expresiones racionales y funciones elementales como exp, convierta la función en una expresión de optimización utilizando fcn2optimexpr. Consulte Convertir una función no lineal en una expresión de optimización y Operaciones compatibles con variables y expresiones de optimización.

Cree opciones ga para utilizar la función de gráfico gaplotbestf.

options = optimoptions("ga","PlotFcn","gaplotbestf");

Resuelva el problema utilizando ga como solucionador.

rng default % For reproducibility
[sol,fval] = solve(prob,"Solver","ga","Options",options)

Solving problem using ga.
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

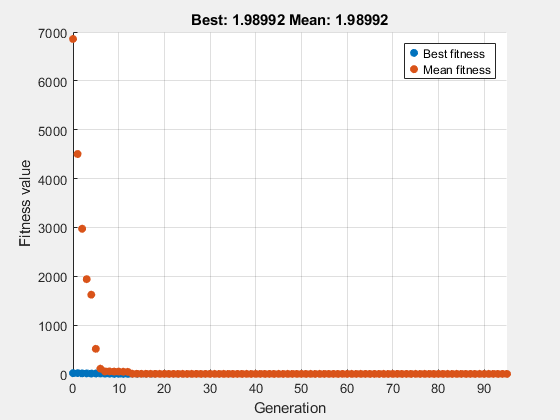
sol = struct with fields:
    x: 0.9950
    y: 0.9950

fval = 
1.9899

¿El valor de la función resultante es el mínimo más bajo? Realice la búsqueda nuevamente. Debido a que ga es un algoritmo estocástico, los resultados pueden diferir.

[sol2,fval2] = solve(prob,"Solver","ga","Options",options)

Solving problem using ga.
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

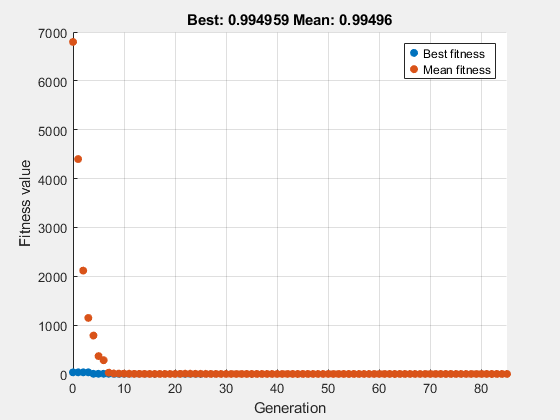
sol2 = struct with fields:
    x: 0.9950
    y: -4.9289e-06

fval2 = 
0.9950

La segunda solución es mejor porque tiene un valor de función más bajo. No se garantiza que una solución devuelta por ga sea una solución global.

Consulte también

ga | fcn2optimexpr | solve

Temas

• Algoritmo genético