Optimizar mediante el uso de enjambre de partículas
Este ejemplo muestra cómo optimizar utilizando el solucionador particleswarm.
La función objetivo en este ejemplo es la quinta función de De Jong, que está disponible cuando ejecuta este ejemplo.
dejong5fcn
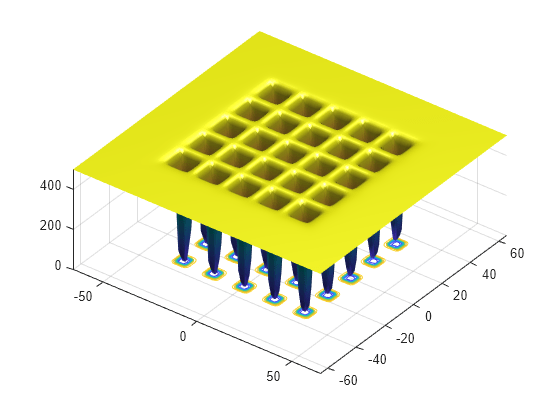
Esta función tiene 25 mínimos locales.
Intente encontrar el mínimo de la función utilizando la configuración predeterminada particleswarm.
fun = @dejong5fcn; nvars = 2; rng default % For reproducibility [x,fval,exitflag] = particleswarm(fun,nvars)
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
x = 1×2
-31.9521 -16.0176
fval = 5.9288
exitflag = 1
¿Es la solución x el óptimo global? No está claro en este momento. Al observar el gráfico de la función se ve que la función tiene mínimos locales para los componentes en el rango [-50,50]. Por lo tanto, restringir el rango de las variables a [-50,50] ayuda al solucionador a localizar un mínimo global.
lb = [-50;-50]; ub = -lb; [x,fval,exitflag] = particleswarm(fun,nvars,lb,ub)
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
x = 1×2
-16.0079 -31.9697
fval = 1.9920
exitflag = 1
Esto parece prometedor: la nueva solución tiene menos fval que la anterior. Pero ¿es x realmente una solución global? Intente minimizar nuevamente con más partículas, para buscar mejor la región.
options = optimoptions('particleswarm','SwarmSize',100); [x,fval,exitflag] = particleswarm(fun,nvars,lb,ub,options)
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
x = 1×2
-31.9781 -31.9784
fval = 0.9980
exitflag = 1
Esto parece aún más prometedor. Pero ¿es esta respuesta una solución global y qué tan precisa es? Vuelva a ejecutar el solucionador con una función híbrida. particleswarm llama a la función híbrida después de que particleswarm finalice sus iteraciones.
options.HybridFcn = @fmincon; [x,fval,exitflag] = particleswarm(fun,nvars,lb,ub,options)
Optimization ended: relative change in the objective value over the last OPTIONS.MaxStallIterations iterations is less than OPTIONS.FunctionTolerance.
x = 1×2
-31.9783 -31.9784
fval = 0.9980
exitflag = 1
particleswarm encontró esencialmente la misma solución que antes. Esto le da cierta confianza de que particleswarm informa un mínimo local y que el x final es la solución global.