Data and Model Objects in System Identification Toolbox
This example shows how to manage data and model objects available in the System Identification Toolbox™. System identification is about building models from data. A data set is characterized by several pieces of information: The input and output signals, the sample time, the variable names and units, and so on. Similarly, the estimated models contain information of different kinds - estimated parameters, their covariance matrices, model structure and so on.
This means that it is suitable and desirable to collect relevant information around data and models into objects. System Identification Toolbox contains a number of such objects, and the basic features of these are described in this example.
The IDDATA Object
First create some data:
u = sign(randn(200,2)); % 2 inputs y = randn(200,1); % 1 output ts = 0.1; % The sample time
To collect the input and the output in one object do
z = iddata(y,u,ts);
The data information is displayed by just typing its name:
z
z =
Time domain data set with 200 samples.
Sample time: 0.1 seconds
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
u2
The data is plotted as iddata by the plot command, as in plot(z). Press a key to continue and advance between the subplots. Here, we plot the channels separately:
plot(z(:,1,1)) % Data subset with Input 1 and Output 1.
plot(z(:,1,2)) % Data subset with Input 2 and Output 1.
To retrieve the outputs and inputs, use
u = z.u; % or, equivalently u = get(z,'u'); y = z.y; % or, equivalently y = get(z,'y');
To select a portion of the data:
zp = z(48:79);
To select the first output and the second input:
zs = z(:,1,2); % The ':' refers to all the data time points.
The sub-selections can be combined:
plot(z(45:54,1,2)) % samples 45 to 54 of response from second input to the first output.
The channels are given default names 'y1', 'u2', etc. This can be changed to any values by
set(z,'InputName',{'Voltage';'Current'},'OutputName','Speed');
Equivalently we could write
z.inputn = {'Voltage';'Current'}; % Autofill is used for properties
z.outputn = 'Speed'; % Upper and lower cases are also ignored
For bookkeeping and plots, also units can be set:
z.InputUnit = {'Volt';'Ampere'};
z.OutputUnit = 'm/s';
z
z =
Time domain data set with 200 samples.
Sample time: 0.1 seconds
Outputs Unit (if specified)
Speed m/s
Inputs Unit (if specified)
Voltage Volt
Current Ampere
All current properties are (as for any object) obtained by get:
get(z)
ans =
struct with fields:
Domain: 'Time'
Name: ''
OutputData: [200×1 double]
y: 'Same as OutputData'
OutputName: {'Speed'}
OutputUnit: {'m/s'}
InputData: [200×2 double]
u: 'Same as InputData'
InputName: {2×1 cell}
InputUnit: {2×1 cell}
Period: [2×1 double]
InterSample: {2×1 cell}
Ts: 0.1000
Tstart: 0.1000
SamplingInstants: [200×1 double]
TimeUnit: 'seconds'
ExperimentName: 'Exp1'
Notes: {}
UserData: []
In addition to the properties discussed so far, we have 'Period' which denotes the period of the input if periodic Period = inf means a non-periodic input:
z.Period
ans = Inf Inf
The intersample behavior of the input may be given as 'zoh' (zero-order-hold, i.e. piecewise constant) or 'foh' (first- order-hold, i.e., piecewise linear). The identification routines use this information to adjust the algorithms.
z.InterSample
ans =
2×1 cell array
{'zoh'}
{'zoh'}
You can add channels (both input and output) by "horizontal concatenation", i.e. z = [z1 z2]:
z2 = iddata(rand(200,1),ones(200,1),0.1,'OutputName','New Output',... 'InputName','New Input'); z3 = [z,z2]
z3 =
Time domain data set with 200 samples.
Sample time: 0.1 seconds
Outputs Unit (if specified)
Speed m/s
New Output
Inputs Unit (if specified)
Voltage Volt
Current Ampere
New Input
Let us plot some of the channels of z3:
plot(z3(:,1,1)) % Data subset with Input 2 and Output 1.

plot(z3(:,2,3)) % Data subset with Input 2 and Output 3.
Generating Inputs
The command idinput generates typical input signals.
u = idinput([30 1 10],'sine'); % 10 periods of 30 samples u = iddata([],u,1,'Period',30) % Making the input an IDDATA object.
u =
Time domain data set with 300 samples.
Sample time: 1 seconds
Inputs Unit (if specified)
u1
SIM applied to an iddata input delivers an iddata output. Let us use sim to obtain the response of an estimated model m using the input u. We also add noise to the model response in accordance with the noise dynamics of the model. We do this by using the "AddNoise" simulation option:
m = idpoly([1 -1.5 0.7],[0 1 0.5]); % This creates a model; see below. options = simOptions; options.AddNoise = true; y = sim(m,u,options) % simulated response produced as an iddata object
y =
Time domain data set with 300 samples.
Sample time: 1 seconds
Name: m
Outputs Unit (if specified)
y1
The simulation input u and the output y may be combined into a single iddata object as follows:
z5 = [y u] % The output-input iddata.
z5 =
Time domain data set with 300 samples.
Sample time: 1 seconds
Name: m
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
More about the iddata object is found under help iddata.
The Linear Model Objects
All models are delivered as MATLAB® objects. There are a few different objects depending on the type of model used, but this is mostly transparent.
load iddata1 m = armax(z1,[2 2 2 1]); % This creates an ARMAX model, delivered as an IDPOLY object
All relevant properties of this model are packaged as one object (here, idpoly). To display it just type its name:
m
m =
Discrete-time ARMAX model: A(z)y(t) = B(z)u(t) + C(z)e(t)
A(z) = 1 - 1.531 z^-1 + 0.7293 z^-2
B(z) = 0.943 z^-1 + 0.5224 z^-2
C(z) = 1 - 1.059 z^-1 + 0.1968 z^-2
Sample time: 0.1 seconds
Parameterization:
Polynomial orders: na=2 nb=2 nc=2 nk=1
Number of free coefficients: 6
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using ARMAX on time domain data "z1".
Fit to estimation data: 76.38% (prediction focus)
FPE: 1.127, MSE: 1.082
Many of the model properties are directly accessible
m.a % The A-polynomial
ans =
1.0000 -1.5312 0.7293
A list of properties is obtained by get:
get(m)
A: [1 -1.5312 0.7293]
B: [0 0.9430 0.5224]
C: [1 -1.0587 0.1968]
D: 1
F: 1
IntegrateNoise: 0
Variable: 'z^-1'
IODelay: 0
Structure: [1×1 pmodel.polynomial]
NoiseVariance: 1.1045
InputDelay: 0
OutputDelay: 0
InputName: {'u1'}
InputUnit: {''}
InputGroup: [1×1 struct]
OutputName: {'y1'}
OutputUnit: {''}
OutputGroup: [1×1 struct]
Notes: [0×1 string]
UserData: []
Name: ''
Ts: 0.1000
TimeUnit: 'seconds'
SamplingGrid: [1×1 struct]
Report: [1×1 idresults.polyest]
Use present to view the estimated parameter covariance as +/- 1 standard deviation uncertainty values on individual parameters:
present(m)
m =
Discrete-time ARMAX model: A(z)y(t) = B(z)u(t) + C(z)e(t)
A(z) = 1 - 1.531 (+/- 0.01801) z^-1 + 0.7293 (+/- 0.01473) z^-2
B(z) = 0.943 (+/- 0.06074) z^-1 + 0.5224 (+/- 0.07818) z^-2
C(z) = 1 - 1.059 (+/- 0.06067) z^-1 + 0.1968 (+/- 0.05957) z^-2
Sample time: 0.1 seconds
Parameterization:
Polynomial orders: na=2 nb=2 nc=2 nk=1
Number of free coefficients: 6
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Termination condition: Near (local) minimum, (norm(g) < tol)..
Number of iterations: 3, Number of function evaluations: 7
Estimated using ARMAX on time domain data "z1".
Fit to estimation data: 76.38% (prediction focus)
FPE: 1.127, MSE: 1.082
More information in model's "Report" property.
Use getpvec to fetch a flat list of all the model parameters, or just the free ones, and their uncertainties. Use getcov to fetch the entire covariance matrix.
[par, dpar] = getpvec(m, 'free') CovFree = getcov(m,'value')
par =
-1.5312
0.7293
0.9430
0.5224
-1.0587
0.1968
dpar =
0.0180
0.0147
0.0607
0.0782
0.0607
0.0596
CovFree =
0.0003 -0.0003 0.0000 0.0007 0.0004 -0.0003
-0.0003 0.0002 -0.0000 -0.0004 -0.0003 0.0002
0.0000 -0.0000 0.0037 -0.0034 -0.0000 0.0001
0.0007 -0.0004 -0.0034 0.0061 0.0008 -0.0005
0.0004 -0.0003 -0.0000 0.0008 0.0037 -0.0032
-0.0003 0.0002 0.0001 -0.0005 -0.0032 0.0035
nf = 0, nd = 0 denote orders of a general linear model, of which the ARMAX model is a special case.
Report contains information about the estimation process:
m.Report m.Report.DataUsed % record of data used for estimation m.Report.Fit % quantitative measures of model quality m.Report.Termination % search termination conditions
ans =
Status: 'Estimated using ARMAX with prediction focus'
Method: 'ARMAX'
InitialCondition: 'zero'
Fit: [1×1 struct]
Parameters: [1×1 struct]
OptionsUsed: [1×1 idoptions.polyest]
RandState: [1×1 struct]
DataUsed: [1×1 struct]
Termination: [1×1 struct]
ans =
struct with fields:
Name: 'z1'
Type: 'Time domain data'
Length: 300
Ts: 0.1000
InterSample: 'zoh'
InputOffset: []
OutputOffset: []
ans =
struct with fields:
FitPercent: 76.3807
LossFcn: 1.0824
MSE: 1.0824
FPE: 1.1266
AIC: 887.1256
AICc: 887.4123
nAIC: 0.1192
BIC: 909.3483
ans =
struct with fields:
WhyStop: 'Near (local) minimum, (norm(g) < tol).'
Iterations: 3
FirstOrderOptimality: 7.2436
FcnCount: 7
UpdateNorm: 0.0067
LastImprovement: 0.0067
To obtain on-line information about the minimization, use the 'Display' estimation option with possible values 'off', 'on', and 'full'. This launches a progress viewer that shows information on the model estimation progress.
Opt = armaxOptions('Display','on'); m1 = armax(z1,[2 2 2 1],Opt);
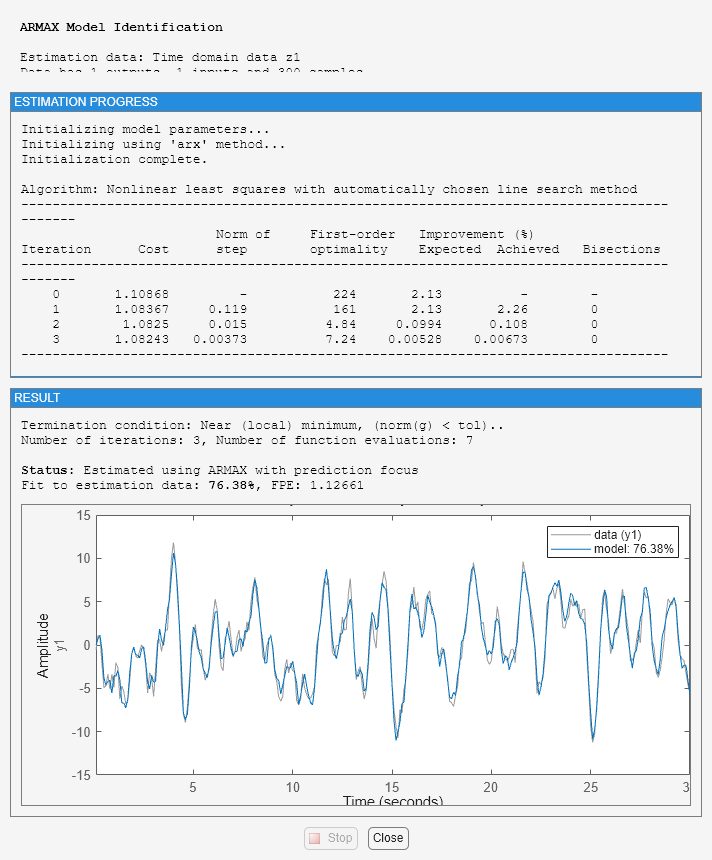
Variants of Linear Models - IDTF, IDPOLY, IDPROC, IDSS and IDGREY
There are several types of linear models. The one above is an example of the idpoly version for polynomial type models. Different variants of polynomial-type models, such as Box-Jenkins models, Output Error models, ARMAX models etc are obtained using the corresponding estimators - bj, oe, armax, arx etc. All of these are presented as idpoly objects.
Other variants are idss for state-space models; idgrey for user-defined structured state-space models; idtf for transfer function models, and idproc for process models (gain+delay+static gain).
The commands to evaluate the model: bode, step, iopzmap, compare, etc, all operate directly on the model objects, for example:
compare(z1,m1)

Transformations to state-space, transfer function and zeros/poles are obtained by idssdata, tfdata and zpkdata:
[num,den] = tfdata(m1,'v')
num =
0 0.9430 0.5224
den =
1.0000 -1.5312 0.7293
The 'v' means that num and den are returned as vectors and not as cell arrays. The cell arrays are useful to handle multivariable systems. To also retrieve the 1 standard deviation uncertainties in the values of num and den use:
[num, den, ~, dnum, dden] = tfdata(m1,'v')
num =
0 0.9430 0.5224
den =
1.0000 -1.5312 0.7293
dnum =
0 0.0607 0.0782
dden =
0 0.0180 0.0147
Transforming Identified Models into Numeric LTIs of Control System Toolbox
The objects also connect directly to the Control System Toolbox™ model objects, like tf, ss, and zpk, and can be converted into these LTI objects, if Control System Toolbox is available. For example, tf converts an idpoly object into a tf object.
CSTBInstalled = exist('tf','class')==8; if CSTBInstalled % check if Control System Toolbox is installed tfm = tf(m1) % convert IDPOLY model m1 into a TF object end
tfm =
From input "u1" to output "y1":
0.943 z^-1 + 0.5224 z^-2
----------------------------
1 - 1.531 z^-1 + 0.7293 z^-2
Sample time: 0.1 seconds
Discrete-time transfer function.
When converting an IDLTI model to the Control Systems Toolbox's LTI models, noise component is not retained. To also include the noise channels as regular inputs of the LTI model, use the 'augmented' flag:
if CSTBInstalled tfm2 = tf(m1,'augmented') end
tfm2 =
From input "u1" to output "y1":
0.943 z^-1 + 0.5224 z^-2
----------------------------
1 - 1.531 z^-1 + 0.7293 z^-2
From input "v@y1" to output "y1":
1.051 - 1.113 z^-1 + 0.2069 z^-2
--------------------------------
1 - 1.531 z^-1 + 0.7293 z^-2
Input groups:
Name Channels
Measured 1
Noise 2
Sample time: 0.1 seconds
Discrete-time transfer function.
The noise channel is named v@y1 in the model tfm2.