PDSCH Throughput for Non-Codebook Based MU-MIMO Transmission Mode 9 (TM9)

Open Script

This example demonstrates how to measure the physical downlink shared channel (PDSCH) throughput performance in a multiuser multiple-input multiple-output (MU-MIMO) scenario with LTE Toolbox™. It models non-codebook based transmission mode, TM9, with block diagonalization [ 1 ]. This example supports both frequency division duplexing (FDD) and time division duplexing (TDD) schemes. It also supports the use of Parallel Computing Toolbox™ to reduce the effective simulation time.

Introduction

In a MU-MIMO scenario, due to the simultaneous transmission of data to multiple users, inter-user interference will be present at the receiver. Inter-user interference at the receiver can be canceled using precoding techniques at the transmitter. Two linear precoding techniques for MU-MIMO transmission are channel inversion and block diagonalization. This example uses block diagonalization precoding. This example measures the PDSCH throughput in a MU-MIMO scenario for a number of signal-to-noise ratio (SNR) points. For information on how to model single-user MIMO (SU-MIMO) in LTE look at the following example: PDSCH Throughput for Non-Codebook Based Precoding Schemes: Port 5 (TM7), Port 7 or 8 or Port 7-8 (TM8), Port 7-14 (TM9 and TM10)

A simple MU-MIMO block diagram with the default simulation configuration parameters used in the example is shown in the following figure.

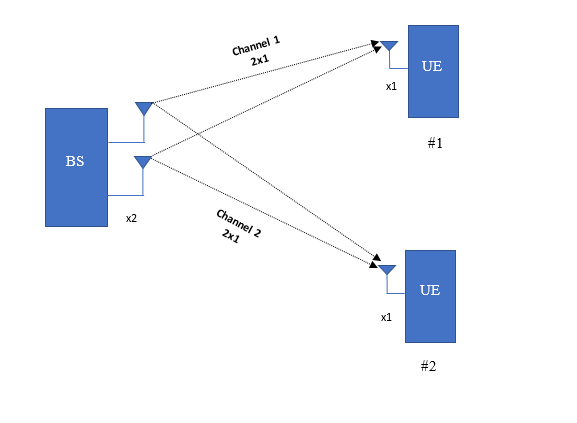
Simulation Configuration

The simulation parameters for the base station and users are configured in this section. The example is executed for a simulation length of two frames for a number of SNR points. Increase NFrames to increase the simulation time and produce statistically significant throughput results. Use the variable SNRIn to set the SNR, it can be an array of values or a scalar. As per the constraints in LTE [ 2 ], this example supports a maximum of 4 users with a maximum of 4 layers across all users. The number of maximum layers per user is 2. The number of transmit antennas should be greater than or equal to the total number of receive antennas across all users.

NFrames = 2;              % Number of frames
SNRIn = [8 14];           % SNR range in dB
NUsers = 2;               % Number of active users
NTxAnts = 2;              % Number of antennas at eNodeB

% Specify UE-specific parameters
muNumLayers = [1 1 1 1];  % Number of layers for a maximum of 4 users
muNumRxAnts = [1 1 1 1];  % Number of receive antennas for a maximum of 4 users
muCodeRate = [0.5 0.5 0.5 0.5]; % Code rate for a maximum of 4 users
muModulation = {'16QAM';'16QAM';'16QAM';'16QAM'}; % Modulation for a maximum of 4 users

The set of parameters required for TM9 is specified below. This example does not perform DCI format decoding; the DCIFormat field is included for completeness. The cell array muPDSCH stores the PDSCH transmission configuration structure for all users.

% Initialize cell arrays of PDSCH transmission configuration structures,
% transport block sizes and coded transport block sizes.
muPDSCH = cell(NUsers,1);
trBlkSizes = cell(NUsers,1);
codedTrBlkSizes = cell(NUsers,1);

simulationParameters = []; % clear simulation parameters
simulationParameters.NDLRB = 50;
simulationParameters.PDSCH.PRBSet = (0)';
simulationParameters.PDSCH.DCIFormat = 'Format2C';
simulationParameters.PDSCH.TxScheme = 'Port7-14';
simulationParameters.PDSCH.NTxAnts = NTxAnts;
simulationParameters.DuplexMode = 'FDD'; % 'FDD', 'TDD'
simulationParameters.TotSubframes = 1;

% PDSCH configuration structure for users based on the common and
% user-specific parameters
ncw = zeros(NUsers,1);
for userIdx = 1:NUsers
    simulationParameters.PDSCH.TargetCodeRate = muCodeRate(userIdx);
    simulationParameters.PDSCH.Modulation = muModulation{userIdx};
    simulationParameters.PDSCH.NLayers = muNumLayers(userIdx);
    % Initialize W to zero
    simulationParameters.PDSCH.W = zeros(muNumLayers(userIdx),NTxAnts);
    % Downlink reference measurement channel configuration
    enb = lteRMCDL(simulationParameters);
    % PDSCH transmission configuration structure for users
    muPDSCH{userIdx}= enb.PDSCH;
    % Number of codewords for users
    ncw(userIdx) = length(muPDSCH{userIdx}.Modulation);
    % Store transport block sizes for users
    trBlkSizes{userIdx} = muPDSCH{userIdx}.TrBlkSizes;
end
% Assign redundancy version sequence
rvSequence = muPDSCH{1}.RVSeq;

Print a summary of some of the more relevant simulation parameters.

hMultiUserParameterSummary(enb,muPDSCH,muNumRxAnts);

 Parameter summary for TM9 MU-MIMO Transmission
------------------------------------------------------------------
                      Duplexing mode: FDD
                   Transmission mode: TM9(MU-MIMO)
                 Transmission scheme: Port7-14
  Number of downlink resource blocks: 50
 Number of allocated resource blocks: 1
         Number of transmit antennas: 2
------------------------------------------------------------------
Number of Transmission layers for UE-1: 1
          Number of codewords for UE-1: 1
   Number of receive antennas for UE-1: 1
               Modulation codeword 1: 16QAM
    Transport block sizes codeword 1:      208     208     208     208     208     208     208     208     208     208
                Code rate codeword 1:   0.5088  0.5088  0.5088  0.5088  0.5088  0.5088  0.5088  0.5088  0.5088  0.5088
------------------------------------------------------------------
Number of Transmission layers for UE-2: 1
          Number of codewords for UE-2: 1
   Number of receive antennas for UE-2: 1
               Modulation codeword 1: 16QAM
    Transport block sizes codeword 1:      208     208     208     208     208     208     208     208     208     208
                Code rate codeword 1:   0.5088  0.5088  0.5088  0.5088  0.5088  0.5088  0.5088  0.5088  0.5088  0.5088

Propagation Channel

The channel model configuration parameters for the channel between the eNodeB and the users are stored in the cell array muChannel. The set of common parameters for each channel is initially specified. The parameters defined here are used with lteFadingChannel during subframe processing.

muChannel  = cell(NUsers,1);
channel = struct;
channel.DelayProfile ='EPA';         % Delay profile
channel.MIMOCorrelation = 'Low';     % Multi-antenna correlation
channel.NTerms = 16;                 % Oscillators used in fading model
channel.ModelType = 'GMEDS';         % Rayleigh fading model type
channel.InitPhase = 'Random';        % Random initial phases
channel.NormalizePathGains = 'On';   % Normalize delay profile power
channel.NormalizeTxAnts = 'On';      % Normalize for transmit antennas

The channel sampling rate depends on the FFT size used in the OFDM modulator. This can be obtained using the function lteOFDMInfo.

ofdmInfo = lteOFDMInfo(enb);
channel.SamplingRate = ofdmInfo.SamplingRate;

% Independent channel configuration parameters for each user
chanSeeds = [1111 2222 3333 4444];  % Channel seed for a maximum of 4 users
dopplerFreq = [5 50 25 15];         % Doppler frequency for a maximum of 4 users
for userIdx = 1:NUsers
    muChannel{userIdx}= channel;
    muChannel{userIdx}.Seed = chanSeeds(userIdx);         % Channel seed
    muChannel{userIdx}.NRxAnts = muNumRxAnts(userIdx);    % Number of receive antennas
    muChannel{userIdx}.DopplerFreq = dopplerFreq(userIdx);% Doppler frequency
end

Processing Chain

To determine the throughput at each SNR point, the subframe-by-subframe PDSCH processing chain includes:

Calculating the Precoding Matrix - A perfect channel estimate is used to calculate the precoding matrix for each user. A detailed explanation of this step is provided in the next section.

Updating Current HARQ Process - Separate HARQ processes are used for each user.

Creating Transmit Waveform - Separate PDSCH symbols are generated for each user. The PDSCH symbols are precoded with the calculated precoding matrix. The precoded PDSCH symbols corresponding to the UEs are combined and OFDM modulated.

Channel Modeling - Pass the waveform through a fading channel to each user and add noise (AWGN)

Performing Synchronization and OFDM Demodulation - Separately carried out for each user. Offset the received symbols to account for a combination of implementation delay and channel delay spread. OFDM demodulate the symbols.

Decoding the PDSCH - Separately carried out for each user. Perfect channel estimate is assumed at the receiver for decoding operations. Obtain an estimate of the received codewords using ltePDSCHDecode to demodulate and descramble the recovered PDSCH symbols for all transmit and receive antenna pairs.

Decoding the DL-SCH and Storing the Block CRC - Separately carried out for each user. Pass the vector of decoded soft bits to lteDLSCHDecode, which decodes the codeword and returns the block CRC error used to determine the throughput of the system.

Precoding Matrix Calculation

The precoding matrix for each user needs to be computed based on the channel estimates between the eNodeB and users. The precoding matrix is calculated using the block diagonalization method. For the computation of the precoding matrix, channel state information (CSI) is required at the transmitter. In this example, for the sake of simplicity, perfect knowledge of the channel between the eNodeB and the users is assumed at the base station.

For TDD, the channel estimates between the eNodeB and the users are estimated in the last UL subframe before a DL subframe. These channel estimates are used to calculate the precoding matrix, W. All subsequent DL subframes (including special subframes) until the next UL subframe are precoded with matrix W.

For FDD, there is a delay of one subframe between the calculation of W and the subframe where it is used. For example, W used in DL subframe n has been calculated with the channel estimates obtained in DL subframe n-1.

The function hMultiUserPrecodingMatrix calculates W using the following steps:

Obtain a perfect channel estimate for the considered subframe for all users
Average the channel estimates for all the allocated RBs
Compute the precoding matrix using the block diagonalization method as per the blkdiagbfweights function.

Note that for an allocation of a single resource block, the precoding matrix will usually be well matched to the channel conditions, with little deviation from the optimal precoding. But as the allocation size increases, the precoding matrix takes into account the average of the channel conditions over the whole allocation. This averaging causes a deviation from the optimal precoding matrix. Therefore, you can expect a degradation in performance as the size of the resource allocation increases.

Processing Loop

The 'for' loop for SNR points processing is included below. To enable the use of parallel computing for increased speed use 'parfor' instead of 'for' in the loop. This requires the Parallel Computing Toolbox. If this is not installed 'parfor' will default to the normal 'for' statement.

% Initialize variables used in the simulation and analysis
maxThroughput = zeros(length(SNRIn),NUsers);
simThroughput = zeros(length(SNRIn),NUsers);
harqProcesses = cell(NUsers,1);
% Initialize cell array for constellation plot
rxConstellation = cell(numel(SNRIn),NUsers,2);
% Copy the channel cell array and cell array of PDSCH transmission
% configuration structure to optimize parallel processing (only if running
% the example with Parallel Computing Toolbox)
muChannelInit = muChannel;
muPDSCHInit = muPDSCH;
% During the simulation, some fields of enb will be updated, make a copy to
% reinitialize it when simulating each SNR point
enbInit = enb;

% For TDD precalculate vector of subframe types: D, S and U for downlink,
% special, and uplink, respectively
if strcmpi(enb.DuplexMode,'TDD')
    subframeType = char(10,1);
    initialSubframeNo = enb.NSubframe;
    for sNo=0:9 % for all subframes in a frame
        enb.NSubframe = sNo;
        duplexInfo = lteDuplexingInfo(enb);
        subframeType(sNo+1) = duplexInfo.SubframeType(1); % first char: D, S or U
    end
    enb.NSubframe = initialSubframeNo;
end

% CFI can be a scalar, or a vector of length 10 (corresponding to a frame)
% if the CFI varies per subframe. If CFI is scalar, create a local copy of
% CFI as a vector (one value per subframe).
if numel(enb.CFI) == 1
    CFI = repmat(enb.CFI,1,10);
else
    CFI = enb.CFI;
end

for snrIdx = 1:numel(SNRIn)          % Comment out for parallel computing
%parfor snrIdx = 1:numel(SNRIn)      % Uncomment for parallel computing

    % Set the random number generator seed depending on the loop variable
    % to ensure independent random streams
    rng(snrIdx,'combRecursive');

    % Reinitialize enb structures (they are modified during
    % each SNR point simulation)
    enb = enbInit;
    % Reinitialize muChannel and muPDSCH cell array
    muChannel = muChannelInit;
    muPDSCH = muPDSCHInit;

    % Initialize the state of all HARQ processes
    harqProcesses = cell(NUsers,1);
    for userIdx = 1:NUsers
        harqProcesses{userIdx} = hNewHARQProcess(enb,muPDSCH{userIdx});
    end
    harqProcessSequence = 1;

    % Set up variables for the main loop
    lastOffset = zeros(NUsers,1);
    frameOffset = zeros(NUsers,1);
    blkCRC = [];
    rxSymbols = cell(NUsers,2); % DL-SCH symbols for constellation plot
    bitTput = cell(NUsers,1);
    txedTrBlkSizes = cell(NUsers,1);
    W = cell(NUsers,1);
    pdschIndices = [];
    pdschRho = 0;

    % Flag to indicate if a precoding matrix cell array W is available.
    isWready = false;
    % Flag to indicate if a subframe is to be processed. Set to true if
    % there is data to be processed in the subframe, i.e. non-zero transport
    % block size.
    processSubframe = false;

    % Main for loop: for all subframes
    for subframeNo = 0:(NFrames*10-1)

        % Update subframe number
        enb.NSubframe = subframeNo;

        % Load CFI for current subframe
        enb.CFI = CFI(mod(subframeNo,length(CFI))+1);

        % Get HARQ process ID for the subframe from HARQ process sequence
        harqID = harqProcessSequence(mod(subframeNo,...
                                       length(harqProcessSequence))+1);

        % Channel fading process time offset for the current subframe and
        % transport block size(s)
        trBlk = zeros(NUsers,2); % User can have maximum 2 transport block
        trBlkNext = zeros(NUsers,2);
        for userIdx = 1:NUsers
            % Initialize channel fading process time offset for each subframe
            muChannel{userIdx}.InitTime = subframeNo/1000;
            trBlk(userIdx,1:ncw(userIdx)) = trBlkSizes{userIdx}(:,mod(subframeNo, 10)+1).';
            % Get transport block for next subframe
            trBlkNext(userIdx,1:ncw(userIdx))= trBlkSizes{userIdx}(:,mod(subframeNo+1,10)+1).';
        end

        % Set the flag to trigger subframe processing
        if isWready && any(trBlk(:))
            processSubframe = true;
        else
            processSubframe = false;
        end

        % Precoding matrix calculation
        if strcmpi(enb.DuplexMode,'TDD')
            % Estimate channel in UL subframe
            if strcmp(subframeType(mod(subframeNo,10)+1),'U')
                processSubframe = false; % UL subframe, no DL data
                % Only perform channel estimate if next subframe is DL
                if strcmp(subframeType(mod((subframeNo+1),10)+1),'D')
                    W = hMultiUserPrecodingMatrix(enb,muPDSCH,muChannel);
                    isWready = true;
                end
            end
        else %FDD

            % Calculate the precoding matrix for next subframe only if it
            % carries data (i.e. non-zero trBlkNext)
            if any(trBlkNext(:))
                W = hMultiUserPrecodingMatrix(enb,muPDSCH,muChannel);
                isWready = true;
            else
                isWready = false;
            end
        end

        % Subframe processing
        if processSubframe

            % In this example, the variables pdschRho and pdschIndices will
            % have the same values for all users
            codedTrBlk = zeros(NUsers,2);
            for userIdx = 1:NUsers
                % Update current HARQ process for all users
                harqProcesses{userIdx}(harqID) = hHARQScheduling( ...
                    harqProcesses{userIdx}(harqID), subframeNo, rvSequence);
                % Map precoding matrix of all users into PDSCH configuration
                % cell array
                muPDSCH{userIdx}.W = W{userIdx};
                % PDSCH resource element power allocation in dB
                pdschRho = muPDSCH{userIdx}.Rho;
                % Generate indices for mapping of PDSCH symbols on resource
                % grid
                [pdschIndices,pdschInfo] = ltePDSCHIndices(enb,...
                    muPDSCH{userIdx},muPDSCH{userIdx}.PRBSet);
                % Obtain coded transport block size
                codedTrBlk(userIdx,1:ncw(userIdx)) =  pdschInfo.G;
            end

            % Generate grid without any PDSCH mapped
            [~,txGrid,enbOut] = lteRMCDLTool(enb,[]);

            % Get the HARQ ID sequence from 'enbOut' for HARQ processing
            harqProcessSequence = enbOut.PDSCH.HARQProcessSequence;

            % Generate complex-valued modulated symbol for PDSCH in multi-user
            % MIMO transmission with block-diagonalization precoding
            pdschSymbols = hMultiUserPDSCH(enb,muPDSCH,codedTrBlk,...
                harqProcesses,harqID);
            powerAdjPerRE = 10^(pdschRho/20);

            % Perform PDSCH symbols mapping on resource grid
            txGrid(pdschIndices) = pdschSymbols*powerAdjPerRE;

            % Perform OFDM modulation
            [waveform,ofdmInfo] = lteOFDMModulate(enb,txGrid);

            % Add 25 sample padding. This is to cover the range of delays
            % expected from channel modeling (a combination of
            % implementation delay and channel delay spread)
            txWaveform = [waveform; zeros(25,NTxAnts)];

            % Calculate noise gain including compensation for downlink
            % power allocation
            SNR = 10^((SNRIn(snrIdx)-muPDSCH{userIdx}.Rho)/20);

            % Normalize noise power to take account of sampling rate,
            % which is a function of the IFFT size used in OFDM
            % modulation, and the number of antennas
            N0 = 1/(sqrt(2.0*NTxAnts*double(ofdmInfo.Nfft))*SNR);

            % Pass the waveform through noisy fading channels and receiver
            % operations for each user
            for userIdx = 1:NUsers

                % Pass data through channel model
                rxWaveform = lteFadingChannel(muChannel{userIdx},txWaveform);

                % Create additive white Gaussian noise
                noise = N0*complex(randn(size(rxWaveform)), ...
                    randn(size(rxWaveform)));

                % Add AWGN to the received time domain waveform
                rxWaveform = rxWaveform + noise;

                % Receiver
                % Synchronization offset, OFDM demodulation,
                % perfect channel estimation, PDSCH and DL-SCH Decoding
                [harqProcesses{userIdx},dlschSymbols,lastOffset(userIdx)]...
                    = hReceiverOperations(enb,muPDSCH{userIdx},rxWaveform,...
                   muChannel{userIdx},harqProcesses{userIdx},trBlk(userIdx,...
                   1:ncw(userIdx)),lastOffset(userIdx),harqID,subframeNo,noise);

                % Store the decoded DLSCH symbols for constellation
                % plotting
                rxSymbols{userIdx,1} = [rxSymbols{userIdx,1}; dlschSymbols{1}(:)];
                if ncw(userIdx)>1
                    rxSymbols{userIdx,2} = [rxSymbols{userIdx,2}; dlschSymbols{2}(:)];
                end

                % Store values to calculate throughput
                % Only for subframes with data
                if(any(trBlk(userIdx,1:ncw(userIdx))) ~= 0)
                    blkCRC = [blkCRC harqProcesses{userIdx}(harqID).blkerr];
                    bitTput{userIdx} = [bitTput{userIdx} ...
                        trBlk(userIdx,1:ncw(userIdx)).*(1-harqProcesses{userIdx}(harqID).blkerr)];
                    txedTrBlkSizes{userIdx} = [txedTrBlkSizes{userIdx} ...
                        trBlk(userIdx,1:ncw(userIdx))];
                end
            end
        end
    end

    % Calculate the maximum and simulated throughput
    maxTput = zeros(NUsers,1);
    simTput = zeros(NUsers,1);
    for userIdx = 1:NUsers
        maxTput(userIdx) = sum(txedTrBlkSizes{userIdx}); % Max possible throughput
        simTput(userIdx) = sum(bitTput{userIdx},2);      % Simulated throughput
        % Display the results dynamically in the command window
        fprintf('\nSNR = %.2f dB. Throughput for UE-%d  %d Frame(s) = %.4f Mbps\n',...
            SNRIn(snrIdx),userIdx,NFrames,1e-6*simTput(userIdx)/(NFrames*10e-3));
        fprintf('SNR = %.2f dB. Throughput(%%) for UE-%d %d Frame(s) = %.4f %%\n',...
            SNRIn(snrIdx),userIdx, NFrames,simTput(userIdx)*100/maxTput(userIdx));
    end

    maxThroughput(snrIdx,:) = maxTput;
    simThroughput(snrIdx,:) = simTput;
    rxConstellation(snrIdx,:,:)= rxSymbols;

end

% Plot received symbol constellation
for snrIdx = 1:numel(SNRIn)
    ii = 1;
    figure;
    for userIdx = 1:NUsers
        subplot(NUsers,max(ncw),ii);
        plot(rxConstellation{snrIdx,userIdx,1},'.r');
        title(['User ' num2str(userIdx) ', Codeword 1, SNR '...
            num2str(SNRIn(snrIdx)) ' dB']);
        xlabel('In-Phase');
        ylabel('Quadrature');
        grid on;
        if size(rxConstellation{snrIdx,userIdx,2})~=0
            ii = ii+1;
            subplot(NUsers,max(ncw),ii);
            plot(rxConstellation{snrIdx,userIdx,2},'.r');
            title(['User ' num2str(userIdx) ', Codeword 2, SNR '...
                num2str(SNRIn(snrIdx)) ' dB']);
            xlabel('In-Phase');
            ylabel('Quadrature');
            grid on;
        end
        ii = ii+1;
    end
end

SNR = 8.00 dB. Throughput for UE-1  2 Frame(s) = 0.0520 Mbps
SNR = 8.00 dB. Throughput(%) for UE-1 2 Frame(s) = 26.3158 %

SNR = 8.00 dB. Throughput for UE-2  2 Frame(s) = 0.1352 Mbps
SNR = 8.00 dB. Throughput(%) for UE-2 2 Frame(s) = 68.4211 %

SNR = 14.00 dB. Throughput for UE-1  2 Frame(s) = 0.1456 Mbps
SNR = 14.00 dB. Throughput(%) for UE-1 2 Frame(s) = 73.6842 %

SNR = 14.00 dB. Throughput for UE-2  2 Frame(s) = 0.1976 Mbps
SNR = 14.00 dB. Throughput(%) for UE-2 2 Frame(s) = 100.0000 %

Throughput Results

The throughput results for all users are displayed in the MATLAB® command window after the simulation for each SNR point is completed. They are also captured in output arrays simThroughput and maxThroughput.

legendString = cell(NUsers,1);
figure;
for userIdx = 1:NUsers
    plot(SNRIn, simThroughput(:,userIdx)*100./maxThroughput(:,userIdx),'*-.');
    hold on;
    legendString{userIdx} = strcat('UE-' ,num2str(userIdx), ': ', ...
        num2str(muNumLayers(userIdx)), ' layer(s), ' ,num2str(NTxAnts), ...
        ' TxAnt(s), ', num2str(muNumRxAnts(userIdx)), ' RxAnt(s)');
end
grid on;
xlabel('SNR (dB)');
ylabel('Throughput (%)');
legend(legendString,'Location','SouthEast');

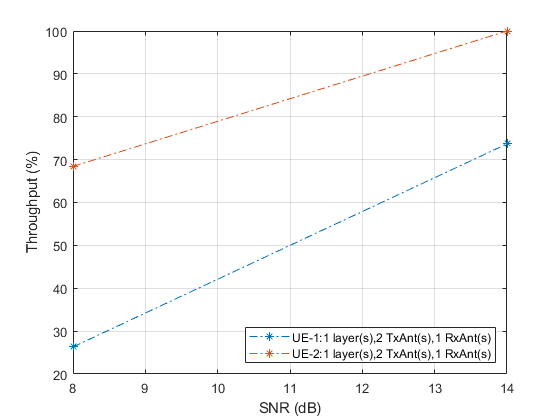
For statistically valid results, the simulation should be run for a larger number of frames. The figure below shows the throughput results when simulating 1000 frames.

Appendix

This example uses the following helper functions:

Selected Bibliography

Spencer Q., A. Swindlehurst, M. Haardt. "Zero-Forcing Methods for Downlink Spatial Multiplexing in Multiuser MIMO Channels." IEEE Transactions on Signal Processing, Vol. 52, No. 2, February 2004, pp. 461-471.
Lim C., T. Yoo, B. Clerckx, B. Lee, B. Shim. "Recent trend of multi-user MIMO in LTE-advanced." IEEE Communications Magazine, March 2013, pp. 127-135.