Downsampling — Aliasing
This example shows how to avoid aliasing when downsampling a signal. If a discrete-time signal's baseband spectral support is not limited to an interval of width radians, downsampling by results in aliasing. Aliasing is the distortion that occurs when overlapping copies of the signal's spectrum are added together. The more the signal's baseband spectral support exceeds radians, the more severe the aliasing. Demonstrate aliasing in a signal downsampled by two. The signal's baseband spectral support exceed radians in width.
Create a signal with baseband spectral support equal to radians. Use fir2 to design the signal. Plot the signal's spectrum. The signal's baseband spectral support exceeds .
f = [0 0.2500 0.5000 0.7500 1.0000]; a = [1.00 0.6667 0.3333 0 0]; nf = 512; b1 = fir2(nf-1,f,a); Hx = fftshift(freqz(b1,1,nf,"whole")); omega = -pi:2*pi/nf:pi-2*pi/nf; plot(omega/pi,abs(Hx)) grid xlabel("\times\pi rad/sample") ylabel("Magnitude")

Downsample the signal by a factor of 2 and plot the downsampled signal's spectrum with the spectrum of the original signal. In addition to an amplitude scaling of the spectrum, the superposition of overlapping spectral replicas causes distortion of the original spectrum for .
y = downsample(b1,2,0); Hy = fftshift(freqz(y,1,nf,"whole")); hold on plot(omega/pi,abs(Hy)) hold off legend("Original","Downsampled") text(2.5/pi*[-1 1],0.35*[1 1], ... {"\downarrow Aliasing","Aliasing \downarrow"}, ... HorizontalAlignment="center")
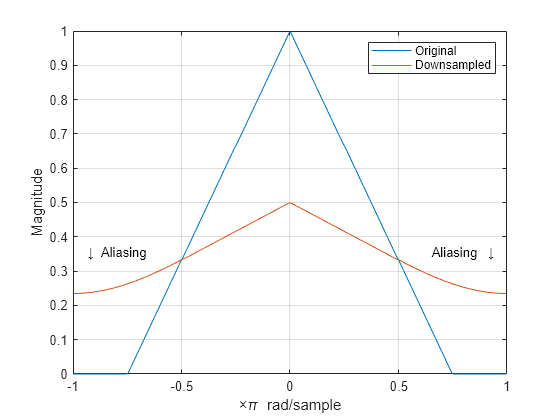
Increase the baseband spectral support of the signal to and downsample the signal by 2. Plot the original spectrum along with the spectrum of the downsampled signal. The increased spectral width results in more pronounced aliasing in the spectrum of the downsampled signal because more signal energy is outside .
f = [0 0.2500 0.5000 0.7500 7/8 1.0000]; a = [1.00 0.7143 0.4286 0.1429 0 0]; b2 = fir2(nf-1,f,a); Hx = fftshift(freqz(b2,1,nf,"whole")); plot(omega/pi,abs(Hx)) grid xlabel("\times\pi rad/sample") ylabel("Magnitude") y = downsample(b2,2,0); Hy = fftshift(freqz(y,1,nf,"whole")); hold on plot(omega/pi,abs(Hy)) hold off legend("Original","Downsampled")
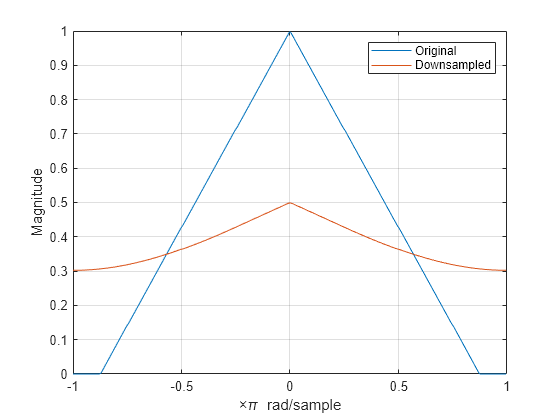
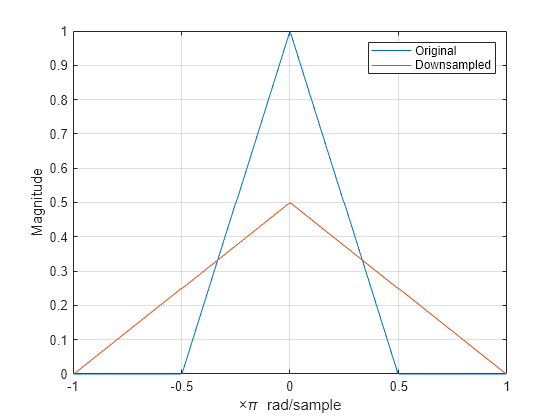
Finally, construct a signal with baseband spectral support limited to . Downsample the signal by a factor of 2 and plot the spectrum of the original and downsampled signals. The downsampled signal is full band. The spectrum of the downsampled signal is a stretched and scaled version of the original spectrum, but the shape is preserved because the spectral copies do not overlap. There is no aliasing.
f = [0 0.250 0.500 0.7500 1]; a = [1.0000 0.5000 0 0 0]; b3 = fir2(nf-1,f,a); Hx = fftshift(freqz(b3,1,nf,"whole")); plot(omega/pi,abs(Hx)) grid xlabel("\times\pi rad/sample") ylabel("Magnitude") y = downsample(b3,2,0); Hy = fftshift(freqz(y,1,nf,"whole")); hold on plot(omega/pi,abs(Hy)) hold off legend("Original","Downsampled")
See Also
downsample | fir2 | freqz
