Medir la potencia de una señal
La potencia de una señal es la suma de los cuadrados absolutos de sus muestras de dominio de tiempo dividida entre la longitud de la señal o, de forma equivalente, el cuadrado de su nivel de RMS. La función bandpower le permite calcular la potencia de la señal en un paso.
Piense en un chirp unitario integrado en ruido blanco gaussiano y muestreado a 1 kHz durante 1,2 segundos. La frecuencia del chirp aumenta en un segundo y pasa de un valor inicial de 100 Hz a 300 Hz. El ruido presenta varianza . Reinicie el generador de números aleatorios para obtener resultados reproducibles.
N = 1200;
Fs = 1000;
t = (0:N-1)/Fs;
sigma = 0.01;
rng('default')
s = chirp(t,100,1,300)+sigma*randn(size(t));Verifique que el cálculo de la potencia dado por bandpower es equivalente a la definición.
pRMS = rms(s)^2
pRMS = 0.5003
powbp = bandpower(s,Fs,[0 Fs/2])
powbp = 0.5005
Utilice la función obw para calcular el ancho de la banda de frecuencia que contiene el 99% de la potencia de la señal, los límites inferior y superior de la banda y la potencia en la banda. La función también representa el cálculo del espectro y anota el ancho de banda ocupado.
obw(s,Fs);
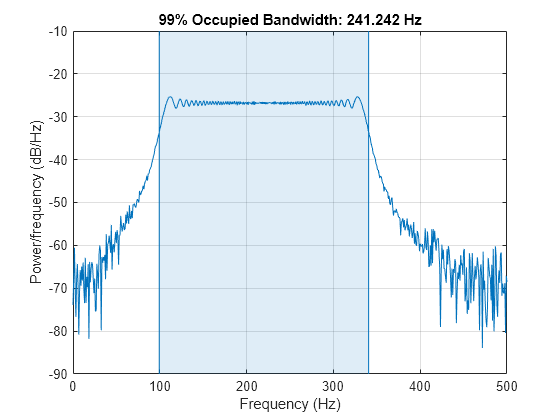
[wd,lo,hi,power] = obw(s,Fs); powtot = power/0.99
powtot = 0.5003
Un amplificador de potencia no lineal recibe una sinusoide de 60 Hz como entrada y devuelve como salida una señal con ruido con distorsión de tercer orden. La señal se muestrea a 3,6 kHz durante dos segundos.
Fs = 3600; t = 0:1/Fs:2-1/Fs; x = sin(2*pi*60*t); y = polyval(ones(1,4),x) + randn(size(x));
Puesto que el amplificador introduce distorsión de tercer orden, se espera que la señal de salida presente:
Un componente fundamental con la misma frecuencia que la entrada: 60 Hz.
Dos armónicas: componentes de frecuencia que doblan o triplican la frecuencia de la entrada: 120 y 180 Hz.
Utilice la función thd para visualizar el espectro de la señal. Anote la fundamental y las armónicas.
thd(y,Fs);

Utilice bandpower para determinar la potencia almacenada en la fundamental y las armónicas. Exprese cada valor como un porcentaje de la potencia total en decibelios. Muestre los valores como tabla.
pwrTot = bandpower(y,Fs,[0 Fs/2]);
Harmonic = {'Fundamental';'First';'Second'};
Freqs = [60 120 180]';
Power = zeros([3 1]);
for k = 1:3
Power(k) = bandpower(y,Fs,Freqs(k)+[-10 10]);
end
Percent = Power/pwrTot*100;
inDB = pow2db(Power);
T = table(Freqs,Power,Percent,inDB,'RowNames',Harmonic)T=3×4 table
Freqs Power Percent inDB
_____ _______ _______ _______
Fundamental 60 1.5777 31.788 1.9804
First 120 0.13141 2.6476 -8.8137
Second 180 0.04672 0.9413 -13.305
Consulte también
bandpower | pow2db | pwelch | snr