Design Controller for Vehicle Platooning
This example shows how to design a controller for vehicle platooning applications. In a platoon of vehicles, every following vehicle maintains a constant spacing from its preceding vehicle. Vehicles travelling in tightly spaced platoons can improve traffic flow, safety, and fuel economy.

Platooning has the following control objectives [1].
Individual vehicle stability — Spacing error for each following vehicle converges to zero if the preceding vehicle is traveling at constant speed.
String stability — Spacing errors do not amplify as they propagate towards the tail of the vehicle string.
For an example that uses the designed controller in a platooning application with vehicle-to-vehicle communication, see Truck Platooning Using Vehicle-to-Vehicle Communication (Automated Driving Toolbox).
Platooning Model
In this example, there are five vehicles in the platoon. Every vehicle is modeled as a truck-trailer system with the following parameters. All lengths are in meters.
L1 = 6; % Truck length L2 = 10; % Trailer length M1 = 1; % Interconnection length
The lead vehicle follows a given acceleration profile. Each trailing vehicle has a controller that controls its acceleration.
Open the Simulink® model.
mdl = "fiveVehiclePlatoon";
open_system(mdl)
Controller Design
In this example, the trailing vehicles all use the same controller design, which has the following structure.
Here:
, , and are the respective acceleration, velocity, and position of the ego vehicle, that is, the trailing vehicle under control.
and are the acceleration and velocity of the vehicle directly in front of the ego vehicle.
and are the acceleration and position of the lead vehicle in the platoon.
Each vehicle obtains this information from onboard sensors and wireless communication with the other vehicles in the platoon.
The parameters for the controller are as follows.
is the desired following distance.
is a constant.
is a constant.
is a PID controller.
The controller minimizes the velocity error using controller , and minimizes the spacing error using .
Define the initial controller parameters.
L = L1 + L2 + M1 + 5; % Front-to-front vehicle spacing C1 = 0.8; % Constant gain K1 = 8; % Constant gain K2 = [2,1]; % PD gains for spacing control [P,D]
Run the simulation.
sim(mdl);


In the top plot, the velocity of each following vehicle converges to the lead velocity. In the bottom plot, the spacing between vehicles converges to the desired spacing.
PID Tuning
To improve performance, you can tune the gains of the PID controller. As an example, tune the spacing PID controller for the 4th vehicle in the platoon.
Open the controller.
open_system(mdl + "/4th with controller/controller/K2")In the block parameters, under Select tuning method, select Transfer Function Based (PID Tuner App). Click Tune.
In the PID Tuner app, tune the response time and transient behavior of the controller. For example, a Response Time seconds and a Transient Behavior factor of 0.6 produce a PID controller with a faster response and no overshoot.

To update the controller parameters in the model, click Update Block.
For this example, open and simulate a Simulink model with the tuned parameters of the 4th controller set.
mdlTuned = "fiveVehiclePlatoonTuned";
open_system(mdlTuned)
sim(mdlTuned);

In the spacing plot, the error for the 4th vehicle converges faster than in the previous simulation.
Since the trailing vehicles use the same controller design, set the gains for the other trailing vehicles to the tuned gains from the 4th vehicle.
Obtained tuned controller gains.
pTuned = get_param(mdlTuned + "/4th with controller/controller/K2","P"); dTuned = get_param(mdlTuned + "/4th with controller/controller/K2","D");
Set the gains in other controllers.
set_param(mdlTuned + "/3rd with controller/controller/K2","P",pTuned) set_param(mdlTuned + "/3rd with controller/controller/K2","D",dTuned) set_param(mdlTuned + "/2nd with controller/controller/K2","P",pTuned) set_param(mdlTuned + "/2nd with controller/controller/K2","D",dTuned) set_param(mdlTuned + "/1st with controller/controller/K2","P",pTuned) set_param(mdlTuned + "/1st with controller/controller/K2","D",dTuned)
Simulate the model with all the trailing vehicle controllers controllers tuned.
sim(mdlTuned);

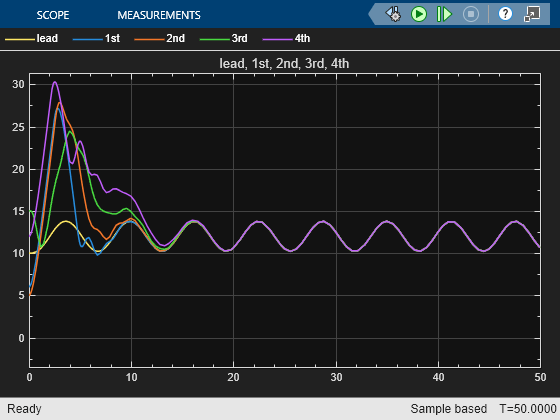
The error for all the trailing vehicles converge faster than in the original simulation.
References
[1] Rajamani, Rajesh. Vehicle Dynamics and Control. 2. ed. Mechanical Engineering Series. New York, NY Heidelberg: Springer, 2012.
See Also
Apps
Blocks
Topics
- Introduction to Model-Based PID Tuning in Simulink
- Truck Platooning Using Vehicle-to-Vehicle Communication (Automated Driving Toolbox)