infer
Infer vector autoregression model (VAR) innovations
Description
Tbl2 = infer(Mdl,Tbl1)Tbl2 containing the multivariate
residuals from evaluating the fully specified VAR(p) model
Mdl at the response variables in the table or timetable of
data Tbl1. (since R2022b)
infer selects the variables in Mdl.SeriesNames or all variables in Tbl1. To select different response variables in Tbl1 at which to evaluate the model, use the ResponseVariables name-value argument.
___ = infer(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name=Value)infer returns the output argument combination for the
corresponding input arguments. For example, infer(Mdl,Y,Y0=PS,X=Exo) computes the
residuals of the VAR(p) model Mdl at the
matrix of response data Y, and specifies the matrix of presample
response data PS and the matrix of exogenous predictor data
Exo.
Supply all input data using the same data type. Specifically:
If you specify the numeric matrix
Y, optional data sets must be numeric arrays and you must use the appropriate name-value argument. For example, to specify a presample, set theY0name-value argument to a numeric matrix of presample data.If you specify the table or timetable
Tbl1, optional data sets must be tables or timetables, respectively, and you must use the appropriate name-value argument. For example, to specify a presample, set thePresamplename-value argument to a table or timetable of presample data.
Examples
Fit a VAR(4) model to the consumer price index (CPI) and unemployment rate data in a matrix. Then, infer the model innovations (residuals) from the estimated model.
Load the Data_USEconModel data set.
load Data_USEconModelPlot the two series on separate plots.
figure plot(DataTimeTable.Time,DataTimeTable.CPIAUCSL) title("Consumer Price Index") ylabel("Index") xlabel("Date")

figure plot(DataTimeTable.Time,DataTimeTable.UNRATE) title("Unemployment Rate") ylabel("Percent") xlabel("Date")

Stabilize the CPI by converting it to a series of growth rates. Synchronize the two series by removing the first observation from the unemployment rate series.
rcpi = price2ret(DataTimeTable.CPIAUCSL); unrate = DataTimeTable.UNRATE(2:end);
Create a default VAR(4) model by using the shorthand syntax.
Mdl = varm(2,4);
Estimate the model using the entire data set.
EstMdl = estimate(Mdl,[rcpi unrate]);
EstMdl is a fully specified, estimated varm model object.
Infer innovations from the estimated model. Supply the same response data that the model was fit to as a numeric matrix.
E = infer(EstMdl,[rcpi unrate]);
E is a 241-by-2 matrix of inferred innovations. The first and second columns contain the residuals corresponding to the CPI growth rate and unemployment rate, respectively.
Alternatively, you can return residuals when you call estimate by supplying an output variable in the fourth position.
Plot the residuals on separate plots. Synchronize the residuals with the dates by removing any missing observations from the data and removing the first Mdl.P dates.
idx = all(~isnan([rcpi unrate]),2); datesr = DataTimeTable.Time(idx); figure plot(datesr((Mdl.P + 1):end),E(:,1)); ylabel("Consumer Price Index") xlabel("Date") title("Residual Plot") hold on yline(0,"r--"); hold off
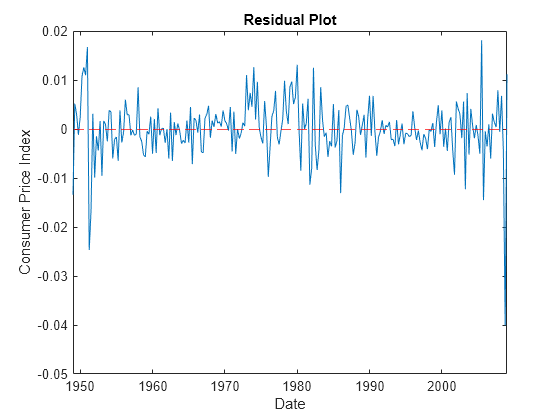
figure plot(datesr((Mdl.P + 1):end),E(:,2)) ylabel("Unemployment Rate") xlabel("Date") title("Residual Plot") hold on yline(0,"r--"); hold off

The residuals corresponding to the CPI growth rate exhibit heteroscedasticity because the series appears to cycle through periods of higher and lower variance.
Since R2022b
Fit a VAR(4) model to the consumer price index (CPI) and unemployment rate data in a timetable. Then, infer the model innovations (residuals) from the estimated model.
Load and Preprocess Data
Load the Data_USEconModel data set. Compute the CPI growth rate. Because the growth rate calculation consumes the earliest observation, include the rate variable in the timetable by prepending the series with NaN.
load Data_USEconModel
DataTimeTable.RCPI = [NaN; price2ret(DataTimeTable.CPIAUCSL)];
numobs = height(DataTimeTable)numobs = 249
Prepare Timetable for Estimation
When you plan to supply a timetable directly to estimate, you must ensure it has all the following characteristics:
All selected response variables are numeric and do not contain any missing values.
The timestamps in the
Timevariable are regular, and they are ascending or descending.
Remove all missing values from the table, relative to the CPI rate (RCPI) and unemployment rate (UNRATE) series.
varnames = ["RCPI" "UNRATE"]; DTT = rmmissing(DataTimeTable,DataVariables=varnames); numobs = height(DTT)
numobs = 245
rmmissing removes the four initial missing observations from the DataTimeTable to create a sub-table DTT. The variables RCPI and UNRATE of DTT do not have any missing observations.
Determine whether the sampling timestamps have a regular frequency and are sorted.
areTimestampsRegular = isregular(DTT,"quarters")areTimestampsRegular = logical
0
areTimestampsSorted = issorted(DTT.Time)
areTimestampsSorted = logical
1
areTimestampsRegular = 0 indicates that the timestamps of DTT are irregular. areTimestampsSorted = 1 indicates that the timestamps are sorted. Macroeconomic series in this example are timestamped at the end of the month. This quality induces an irregularly measured series.
Remedy the time irregularity by shifting all dates to the first day of the quarter.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt; areTimestampsRegular = isregular(DTT,"quarters")
areTimestampsRegular = logical
1
DTT is regular with respect to time.
Create Model Template for Estimation
Create a default VAR(4) model by using the shorthand syntax. Specify the response variable names.
Mdl = varm(2,4); Mdl.SeriesNames = varnames;
Fit Model to Data
Estimate the model. Pass the entire timetable DTT. By default, estimate selects the response variables in Mdl.SeriesNames to fit to the model. Alternatively, you can use the ResponseVariables name-value argument.
EstMdl = estimate(Mdl,DTT);
Compute Residuals
Infer innovations from the estimated model. Supply the same response data that the model was fit to as a timetable. By default, infer selects the variables to use from EstMdl.SeriesNames.
Tbl = infer(EstMdl,DTT); head(Tbl)
Time COE CPIAUCSL FEDFUNDS GCE GDP GDPDEF GPDI GS10 HOANBS M1SL M2SL PCEC TB3MS UNRATE RCPI RCPI_Residuals UNRATE_Residuals
_____ _____ ________ ________ ____ _____ ______ ____ ____ ______ ____ ____ _____ _____ ______ __________ ______________ ________________
Q1-49 144.1 23.91 NaN 45.6 270 16.531 40.9 NaN 53.961 NaN NaN 177 1.17 5 -0.0058382 -0.013422 0.64674
Q2-49 141.9 23.92 NaN 47.3 266.2 16.35 34 NaN 53.058 NaN NaN 178.6 1.17 6.2 0.00041815 0.0051673 0.6439
Q3-49 141 23.75 NaN 47.2 267.7 16.256 37.3 NaN 52.501 NaN NaN 178 1.07 6.6 -0.0071324 0.0030175 -0.099092
Q4-49 140.5 23.61 NaN 46.6 265.2 16.272 35.2 NaN 52.291 NaN NaN 180.4 1.1 6.6 -0.0059122 -0.001196 -0.0066535
Q1-50 144.6 23.64 NaN 45.6 275.2 16.222 44.4 NaN 52.696 NaN NaN 183.1 1.12 6.3 0.0012698 0.0024607 -0.013354
Q2-50 150.6 23.88 NaN 46.1 284.6 16.286 49.9 NaN 53.997 NaN NaN 187 1.15 5.4 0.010101 0.010823 -0.53098
Q3-50 159 24.34 NaN 45.9 302 16.63 56.1 NaN 55.7 NaN NaN 200.7 1.3 4.4 0.01908 0.012566 -0.38177
Q4-50 166.9 24.98 NaN 49.5 313.4 16.95 65.9 NaN 56.213 NaN NaN 198.1 1.34 4.3 0.025954 0.010998 0.50761
size(Tbl)
ans = 1×2
241 17
Tbl is a 241-by-17 timetable of variables in DTT and estimated model residuals, RCPI_Residuals and UNRATE_Residuals.
Alternatively, you can return residuals when you call estimate by supplying an output variable in the fourth position.
Since R2022b
Estimate a VAR(4) model of the consumer price index (CPI), the unemployment rate, and the gross domestic product (GDP). Include a linear regression component containing the current quarter and the last four quarters of government consumption expenditures and investment (GCE). Infer model innovations.
Load the Data_USEconModel data set. Compute the real GDP.
load Data_USEconModel
DataTimeTable.RGDP = DataTimeTable.GDP./DataTimeTable.GDPDEF*100;Plot all variables on separate plots.
figure tiledlayout(2,2) nexttile plot(DataTimeTable.Time,DataTimeTable.CPIAUCSL); ylabel("Index") title("Consumer Price Index") nexttile plot(DataTimeTable.Time,DataTimeTable.UNRATE); ylabel("Percent") title("Unemployment Rate") nexttile plot(DataTimeTable.Time,DataTimeTable.RGDP); ylabel("Output") title("Real Gross Domestic Product") nexttile plot(DataTimeTable.Time,DataTimeTable.GCE); ylabel("Billions of $") title("Government Expenditures")
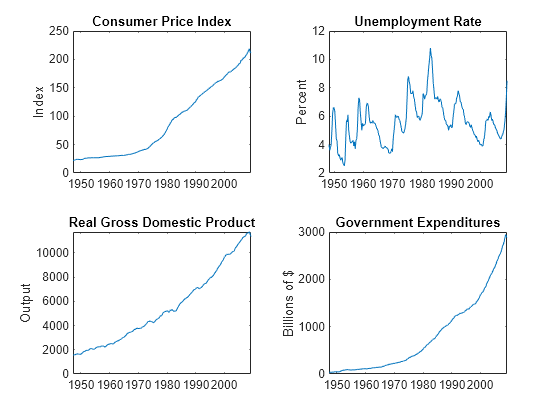
Stabilize the CPI, GDP, and GCE by converting each to a series of growth rates. Synchronize the unemployment rate series with the others by removing its first observation.
varnames = ["CPIAUCSL" "RGDP" "GCE"]; DTT = varfun(@price2ret,DataTimeTable,InputVariables=varnames); DTT.Properties.VariableNames = varnames; DTT.UNRATE = DataTimeTable.UNRATE(2:end);
Make the time base regular.
dt = DTT.Time; dt = dateshift(dt,"start","quarter"); DTT.Time = dt;
Expand the GCE rate series to a matrix that includes the first lagged series through the fourth lag series.
RGCELags = lagmatrix(DTT,1:4,DataVariables="GCE");
DTT = [DTT RGCELags];
DTT = rmmissing(DTT);Create a default VAR(4) model by using the shorthand syntax. Specify the response variable names.
Mdl = varm(3,4); Mdl.SeriesNames = ["CPIAUCSL" "UNRATE" "RGDP"];
Estimate the model using the entire sample. Specify the GCE and its lags as exogenous predictor data for the regression component.
prednames = contains(DTT.Properties.VariableNames,"GCE");
EstMdl = estimate(Mdl,DTT,PredictorVariables=prednames);Infer innovations from the estimated model. Supply the predictor data. Return the loglikelihood objective function value.
[Tbl,logL] = infer(EstMdl,DTT,PredictorVariables=prednames); size(Tbl)
ans = 1×2
240 11
head(Tbl)
Time CPIAUCSL RGDP GCE UNRATE Lag1GCE Lag2GCE Lag3GCE Lag4GCE CPIAUCSL_Residuals UNRATE_Residuals RGDP_Residuals
_____ __________ __________ __________ ______ __________ __________ __________ __________ __________________ ________________ ______________
Q1-49 0.00041815 -0.0031645 0.036603 6.2 0.047147 0.04948 0.04193 0.054347 0.0053457 0.6564 -0.0053201
Q2-49 -0.0071324 0.011385 -0.0021164 6.6 0.036603 0.047147 0.04948 0.04193 0.0088626 -0.034796 0.010153
Q3-49 -0.0059122 -0.010366 -0.012793 6.6 -0.0021164 0.036603 0.047147 0.04948 0.0029402 0.11695 -0.02318
Q4-49 0.0012698 0.040091 -0.021693 6.3 -0.012793 -0.0021164 0.036603 0.047147 0.0040774 -0.2343 0.026583
Q1-50 0.010101 0.029649 0.010905 5.4 -0.021693 -0.012793 -0.0021164 0.036603 0.0046233 -0.18043 0.0091538
Q2-50 0.01908 0.03844 -0.0043478 4.4 0.010905 -0.021693 -0.012793 -0.0021164 0.015141 -0.34049 0.019797
Q3-50 0.025954 0.017994 0.075508 4.3 -0.0043478 0.010905 -0.021693 -0.012793 0.0041785 0.87368 -0.011263
Q4-50 0.035395 0.01197 0.14807 3.4 0.075508 -0.0043478 0.010905 -0.021693 0.011772 -0.49694 -0.0044563
logL
logL = 1.7056e+03
Tbl is a 240-by-11 timetable of data and inferred innovations from the estimated model (residuals).
Plot the residuals on separate plots.
idx = endsWith(Tbl.Properties.VariableNames,"_Residuals"); resvars = Tbl.Properties.VariableNames(idx); titles = "Residuals: " + EstMdl.SeriesNames; figure tiledlayout(2,2) for j = 1:Mdl.NumSeries nexttile plot(Tbl.Time,Tbl{:,resvars(j)}); xlabel("Date"); title(titles(j)); hold on yline(0,"r--"); hold off end
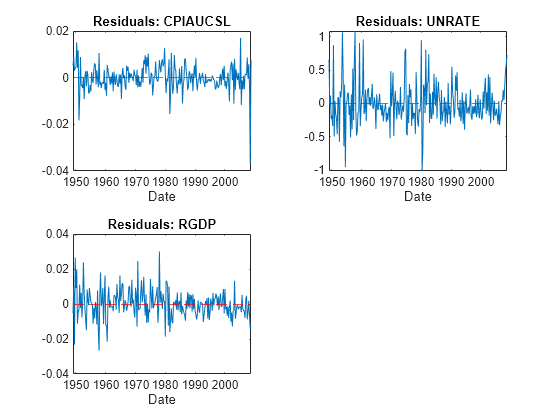
The residuals corresponding to the CPI and GDP growth rates exhibit heteroscedasticity because the CPI series appears to cycle through periods of higher and lower variance. Also, the first half of the GDP series seems to have higher variance than the latter half.
Input Arguments
Response data, specified as a
numobs-by-numseries numeric matrix or a
numobs-by-numseries-by-numpaths
numeric array.
numobs is the sample size. numseries is the
number of response series (Mdl.NumSeries).
numpaths is the number of response paths.
Rows correspond to observations, and the last row contains the latest observation.
Y represents the continuation of the presample response series in
Y0.
Columns must correspond to the response variable names in
Mdl.SeriesNames.
Pages correspond to separate, independent numseries-dimensional
paths. Among all pages, responses in a particular row occur at the same time.
Data Types: double
Since R2022b
Time series data containing observed response variables
yt and, optionally, predictor
variables xt for a model with a regression
component, specified as a table or timetable with numvars variables
and numobs rows.
Each selected response variable is a
numobs-by-numpaths numeric matrix, and each
selected predictor variable is a numeric vector. Each row is an observation, and
measurements in each row occur simultaneously. You can optionally specify
numseries response variables by using the
ResponseVariables name-value argument, and you can specify
numpreds predictor variables by using the
PredictorVariables name-value argument.
Paths (columns) within a particular response variable are independent, but path
jjnumpaths.
If Tbl1 is a timetable, it must represent a sample with a regular
datetime time step (see isregular), and the datetime vector
Tbl1.Time must be ascending or descending.
If Tbl1 is a table, the last row contains the latest
observation.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: infer(Mdl,Y,Y0=PS,X=Exo) computes the residuals of the
VAR(p) model Mdl at the matrix of response
data Y, and specifies the matrix of presample response data
PS and the matrix of exogenous predictor data
Exo.
Since R2022b
Variables to select from Tbl1 to treat as response variables
yt, specified as one of the following
data types:
String vector or cell vector of character vectors containing
numseriesvariable names inTbl1.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromTbl1.Properties.VariableNamesA length
numvarslogical vector, whereResponseVariables(selects variablej) = truejTbl1.Properties.VariableNames, andsum(ResponseVariables)isnumseries
The selected variables must be numeric vectors (single path) or matrices (columns
represent multiple independent paths) of the same width, and cannot contain missing
values (NaN).
If the number of variables in Tbl1 matches
Mdl.NumSeries, the default specifies all variables in
Tbl1. If the number of variables in Tbl1
exceeds Mdl.NumSeries, the default matches variables in
Tbl1 to names in Mdl.SeriesNames.
Example: ResponseVariables=["GDP" "CPI"]
Example: ResponseVariables=[true false true false] or
ResponseVariable=[1 3] selects the first and third table
variables as the response variables.
Data Types: double | logical | char | cell | string
Presample responses that provide initial values for the model
Mdl, specified as a
numpreobs-by-numseries numeric matrix or a
numpreobs-by-numseries-by-numprepaths
numeric array. Use Y0 only when you supply a numeric array of
response data Y.
numpreobs is the number of presample observations.
numprepaths is the number of presample response paths.
Each row is a presample observation, and measurements in each row, among all pages,
occur simultaneously. The last row contains the latest presample observation.
Y0 must have at least Mdl.P rows. If you
supply more rows than necessary, infer uses the latest
Mdl.P observations only.
Each column corresponds to the response series associated with the respective response
series in Y.
Pages correspond to separate, independent paths.
If
Y0is a matrix,inferapplies it to each path (page) inY. Therefore, all paths inYderive from common initial conditions.Otherwise,
inferappliesY0(:,:,toj)Y(:,:,.j)Y0must have at leastnumpathspages, andinferuses only the firstnumpathspages.
By default, infer uses the first Mdl.P
observations, for example, Y(1:Mdl.P,:), as a presample. This action
reduces the effective sample size.
Data Types: double
Since R2022b
Presample data that provides initial values for the model Mdl,
specified as a table or timetable, the same type as Tbl1, with
numprevars variables and numpreobs
rows.
Each row is a presample observation, and measurements in each row, among all paths,
occur simultaneously. numpreobs must be at least
Mdl.P. If you supply more rows than necessary,
infer uses the latest Mdl.P
observations only.
Each variable is a numpreobs-by-numprepaths
numeric matrix. Variables correspond to the response series associated with the
respective response variable in Tbl1. To control presample variable
selection, see the optional PresampleResponseVariables name-value
argument.
For each variable, columns are separate, independent paths.
If variables are vectors,
inferapplies them to each path inTbl1to produce the corresponding residuals inTbl2. Therefore, all response paths derive from common initial conditions.Otherwise, for each variable
ResponseKjinferappliesPresample.to produceResponseK(:,j)Tbl2.. Variables must have at leastResponseK(:,j)numpathscolumns, andinferuses only the firstnumpathscolumns.
If Presample is a timetable, all the following conditions must be true:
Presamplemust represent a sample with a regular datetime time step (seeisregular).The inputs
Tbl1andPresamplemust be consistent in time such thatPresampleimmediately precedesTbl1with respect to the sampling frequency and order.The datetime vector of sample timestamps
Presample.Timemust be ascending or descending.
If Presample is a table, the last row contains the latest
presample observation.
By default, infer uses the first or earliest
Mdl.P observations in Tbl1 as a presample,
and then it fits the model to the remaining numobs – Mdl.P
observations. This action reduces the effective sample size.
Since R2022b
Variables to select from Presample to use
for presample data, specified as one of the
following data types:
String vector or cell vector of character vectors containing
numseriesvariable names inPresample.Properties.VariableNamesA length
numseriesvector of unique indices (integers) of variables to select fromPresample.Properties.VariableNamesA length
numvarslogical vector, wherePresampleResponseVariables(selects variablej) = truejPresample.Properties.VariableNames, andsum(PresampleResponseVariables)isnumseries
The selected variables must be numeric vectors (single path)
or matrices (columns represent multiple independent
paths) of the same width, and cannot contain missing
values (NaN).
PresampleResponseNames does not need to
contain the same names as in
Tbl1;
infer uses the data in
selected variable
PresampleResponseVariables(
as a presample for the response variable
corresponding to
j)ResponseVariables(.j)
The default specifies the same response variables as those
selected from Tbl1 (see
ResponseVariables).
Example: PresampleResponseVariables=["GDP"
"CPI"]
Example: PresampleResponseVariables=[true false true
false] or
PresampleResponseVariable=[1 3]
selects the first and third table variables for
presample data.
Data Types: double | logical | char | cell | string
Predictor data xt for the regression
component in the model, specified as a numeric matrix containing
numpreds columns. Use X only when you supply a
numeric array of response data Y.
numpreds is the number of predictor variables
(size(Mdl.Beta,2)).
Each row corresponds to an observation, and measurements in each row occur
simultaneously. The last row contains the latest observation. X must
have at least as many observations as Y. If you supply more rows
than necessary, infer uses only the latest observations.
infer does not use the regression component in the
presample period.
If you specify a numeric array for a presample by using
Y0,Xmust have at leastnumobsrows (seeY).Otherwise,
Xmust have at leastnumobs–Mdl.Pobservations to account for the default presample removal fromY.
Each column is an individual predictor variable. All predictor variables are present in the regression component of each response equation.
infer applies X to each path (page) in
Y; that is, X represents one path of
observed predictors.
By default, infer excludes the regression component,
regardless of its presence in Mdl.
Data Types: double
Since R2022b
Variables to select from Tbl1 to treat as exogenous predictor variables
xt, specified as one of the following data types:
String vector or cell vector of character vectors containing
numpredsvariable names inTbl1.Properties.VariableNamesA length
numpredsvector of unique indices (integers) of variables to select fromTbl1.Properties.VariableNamesA length
numvarslogical vector, wherePredictorVariables(selects variablej) = truejTbl1.Properties.VariableNames, andsum(PredictorVariables)isnumpreds
The selected variables must be numeric vectors and cannot contain missing values
(NaN).
By default, infer excludes the regression component, regardless
of its presence in Mdl.
Example: PredictorVariables=["M1SL" "TB3MS" "UNRATE"]
Example: PredictorVariables=[true false true false] or
PredictorVariable=[1 3] selects the first and third table variables to
supply the predictor data.
Data Types: double | logical | char | cell | string
Note
NaNvalues inY,Y0, andXindicate missing values.inferremoves missing values from the data by list-wise deletion.If
Yis a 3-D array, theninferhorizontally concatenates the pages ofYto form anumobs-by-(numpaths*numseries + numpreds)matrix.If a regression component is present, then
inferhorizontally concatenatesXtoYto form anumobs-by-numpaths*numseries + 1matrix.inferassumes that the last rows of each series occur at the same time.inferremoves any row that contains at least oneNaNfrom the concatenated data.inferapplies steps 1 and 3 to the presample paths inY0.
This process ensures that the inferred output innovations of each path are the same size and are based on the same observation times. In the case of missing observations, the results obtained from multiple paths of
Ycan differ from the results obtained from each path individually.This type of data reduction reduces the effective sample size.
inferissues an error when any table or timetable input contains missing values.
Output Arguments
Inferred multivariate innovations series, returned as either a numeric matrix, or as a
numeric array that contains columns and pages corresponding to Y.
infer returns E only when you supply a
matrix of response data Y.
If you specify
Y0, thenEhasnumobsrows (seeY).Otherwise,
Ehasnumobs–Mdl.Prows to account for the presample removal.
Since R2022b
Inferred multivariate innovations series and other variables, returned as a table or
timetable, the same data type as Tbl1.
infer returns Tbl2 only when you
supply the input Tbl1.
Tbl2 contains the inferred innovation paths E
from evaluating the model Mdl at the paths of selected response
variables Y, and it contains all variables in
Tbl1. infer names the innovation
variable corresponding to variable
ResponseJTbl1
ResponseJ_ResidualsTbl1 is
GDP, Tbl2 contains a variable for the
residuals in the response equation of GDP with the name
GDP_Residuals.
If you specify presample response data, Tbl2 and
Tbl1 have the same number of rows, and their rows correspond.
Otherwise, because infer removes initial observations from
Tbl1 for the required presample by default,
Tbl2 has numobs – Mdl.P rows to account for
that removal.
If Tbl1 is a timetable, Tbl1 and
Tbl2 have the same row order, either ascending or
descending.
Loglikelihood objective function value, returned as a numeric scalar or a
numpaths-element numeric vector.
logL( corresponds to the
response path in j)Y(:,:, or the path
(column) j)jTbl1.
Algorithms
Suppose Y, Y0, and X are the
response, presample response, and predictor data specified by the numeric data inputs in
Y, Y0, and X, or the
selected variables from the input tables or timetables Tbl1 and
Presample.
inferinfers innovations by evaluating the VAR modelMdl, specifically,inferuses this process to determine the time origin t0 of models that include linear time trends.If you do not specify
Y0, then t0 = 0.Otherwise,
infersets t0 tosize(Y0,1)–Mdl.P. Therefore, the times in the trend component are t = t0 + 1, t0 + 2,..., t0 +numobs, wherenumobsis the effective sample size (size(Y,1)afterinferremoves missing values). This convention is consistent with the default behavior of model estimation in whichestimateremoves the firstMdl.Presponses, reducing the effective sample size. Althoughinferexplicitly uses the firstMdl.Ppresample responses inY0to initialize the model, the total number of observations inY0andY(excluding missing values) determines t0.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.
[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.
[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin: Springer, 2005.
Version History
Introduced in R2017aIn addition to accepting input data in numeric arrays,
infer accepts input data in tables and timetables. infer chooses default series on which to operate, but you can use the following name-value arguments to select variables.
ResponseVariablesspecifies the response series names in the input data from which residuals are inferred.PredictorVariablesspecifies the predictor series names in the input data for a model regression component.Presamplespecifies the input table or timetable of presample response data.PresampleResponseVariablesspecifies the response series names fromPresample.
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)