optByBatesNI
Option price by Bates model using numerical integration
Syntax
Description
Price = optByBatesNI(Rate,AssetPrice,Settle,Maturity,OptSpec,Strike,V0,ThetaV,Kappa,SigmaV,RhoSV,MeanJ,JumpVol,JumpFreq)
Note
Alternatively, you can use the Vanilla object to price
vanilla options. For more information, see Get Started with Workflows Using Object-Based Framework for Pricing Financial Instruments.
Price = optByBatesNI(___,Name,Value)
Examples
optByBatesNI uses numerical integration to compute option prices and then plot an option price surface.
Define Option Variables and Bates Model Parameters
AssetPrice = 80;
Rate = 0.03;
DividendYield = 0.02;
OptSpec = 'call';
V0 = 0.04;
ThetaV = 0.05;
Kappa = 1.0;
SigmaV = 0.2;
RhoSV = -0.7;
MeanJ = 0.02;
JumpVol = 0.08;
JumpFreq = 2;Compute the Option Price for a Single Strike
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 6); Strike = 80; Call = optByBatesNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, V0, ... ThetaV, Kappa, SigmaV, RhoSV, MeanJ, JumpVol, JumpFreq, ... 'DividendYield', DividendYield)
Call = 5.3484
Compute the Option Prices for a Vector of Strikes
The Strike input can be a vector.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 6); Strike = (76:2:84)'; Call = optByBatesNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, V0, ... ThetaV, Kappa, SigmaV, RhoSV, MeanJ, JumpVol, JumpFreq, ... 'DividendYield', DividendYield)
Call = 5×1
7.5765
6.4020
5.3484
4.4173
3.6073
Compute the Option Prices for a Vector of Strikes and a Vector of Dates of the Same Lengths
Use the Strike input to specify the strikes. Also, the Maturity input can be a vector, but it must match the length of the Strike vector if the ExpandOutput name-value pair argument is not set to "true".
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, [12 18 24 30 36]); % Five maturities Strike = [76 78 80 82 84]'; % Five strikes Call = optByBatesNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, V0, ... ThetaV, Kappa, SigmaV, RhoSV, MeanJ, JumpVol, JumpFreq, ... 'DividendYield', DividendYield) % Five values in vector output
Call = 5×1
9.7516
10.3931
10.8865
11.2990
11.6491
Expand the Output for a Surface
Set the ExpandOutput name-value pair argument to "true" to expand the output into a NStrikes-by-NMaturities matrix. In this case, it is a square matrix.
Call = optByBatesNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, V0, ... ThetaV, Kappa, SigmaV, RhoSV, MeanJ, JumpVol, JumpFreq, ... 'DividendYield', DividendYield, 'ExpandOutput', true) % (5 x 5) matrix output
Call = 5×5
9.7516 11.4387 12.8395 14.0588 15.1361
8.6554 10.3931 11.8344 13.0890 14.1980
7.6432 9.4149 10.8865 12.1693 13.3046
6.7153 8.5035 9.9951 11.2990 12.4553
5.8705 7.6581 9.1594 10.4771 11.6491
Compute the Option Prices for a Vector of Strikes and a Vector of Dates of Different Lengths
When ExpandOutput is "true", NStrikes do not have to match NMaturities (that is, the output NStrikes-by-NMaturities matrix can be rectangular).
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 12*(0.5:0.5:3)'); % Six maturities Strike = (76:2:84)'; % Five strikes Call = optByBatesNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, V0, ... ThetaV, Kappa, SigmaV, RhoSV, MeanJ, JumpVol, JumpFreq, ... 'DividendYield', DividendYield, 'ExpandOutput', true) % (5 x 6) matrix output
Call = 5×6
7.5765 9.7516 11.4387 12.8395 14.0588 15.1361
6.4020 8.6554 10.3931 11.8344 13.0890 14.1980
5.3484 7.6432 9.4149 10.8865 12.1693 13.3046
4.4173 6.7153 8.5035 9.9951 11.2990 12.4553
3.6073 5.8705 7.6581 9.1594 10.4771 11.6491
Compute Option Prices for a Vector of Strikes and a Vector of Asset Prices
When ExpandOutput is "true", the output can also be a NStrikes-by-NAssetPrices rectangular matrix by accepting a vector of asset prices.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 12); % Single maturity ManyAssetPrices = [70 75 80 85]; % Four asset prices Strike = (76:2:84)'; % Five strikes Call = optByBatesNI(Rate, ManyAssetPrices, Settle, Maturity, OptSpec, Strike, V0, ... ThetaV, Kappa, SigmaV, RhoSV, MeanJ, JumpVol, JumpFreq, ... 'DividendYield', DividendYield, 'ExpandOutput', true) % (5 x 4) matrix output
Call = 5×4
4.2033 6.6918 9.7516 13.2808
3.5558 5.8111 8.6554 11.9993
2.9906 5.0181 7.6432 10.7934
2.5018 4.3096 6.7153 9.6651
2.0825 3.6818 5.8705 8.6158
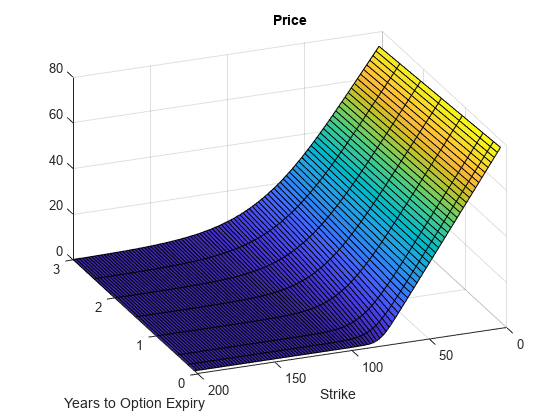
Plot an Option Price Surface
The Strike and Maturity inputs can be vectors. Set ExpandOutput to "true" to output the surface as a NStrikes-by-NMaturities matrix.
Settle = datetime(2017,6,29); Maturity = datemnth(Settle, 12*[1/12 0.25 (0.5:0.5:3)]'); Times = yearfrac(Settle, Maturity); Strike = (2:2:200)'; Call = optByBatesNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, V0, ... ThetaV, Kappa, SigmaV, RhoSV, MeanJ, JumpVol, JumpFreq, ... 'DividendYield', DividendYield, 'ExpandOutput', true); [X,Y] = meshgrid(Times,Strike); figure; surf(X,Y,Call); title('Price'); xlabel('Years to Option Expiry'); ylabel('Strike'); view(-112,34); xlim([0 Times(end)]); zlim([0 80]);
Input Arguments
Continuously compounded risk-free interest rate, specified as a scalar decimal value.
Data Types: double
Current underlying asset price, specified as numeric value using a scalar or a
NINST-by-1 or
NColumns-by-1 vector.
For more information on the proper dimensions for AssetPrice,
see the name-value pair argument ExpandOutput.
Data Types: double
Option settlement date, specified as a
NINST-by-1 or
NColumns-by-1 vector using a datetime array,
string array, or date character vectors. The Settle date must be
before the Maturity date.
To support existing code, optByBatesNI also
accepts serial date numbers as inputs, but they are not recommended.
For more information on the proper dimensions for Settle, see
the name-value pair argument ExpandOutput.
Option maturity date, specified as a
NINST-by-1 or
NColumns-by-1 vector using a datetime array,
string array, or date character vectors.
To support existing code, optByBatesNI also
accepts serial date numbers as inputs, but they are not recommended.
For more information on the proper dimensions for Maturity, see
the name-value pair argument ExpandOutput.
Definition of the option, specified as a
NINST-by-1 or
NColumns-by-1 vector using a cell array of
character vectors or string arrays with values 'call' or
'put'.
For more information on the proper dimensions for OptSpec, see
the name-value pair argument ExpandOutput.
Data Types: cell | string
Option strike price value, specified as a
NINST-by-1,
NRows-by-1,
NRows-by-NColumns vector of strike
prices.
For more information on the proper dimensions for Strike, see
the name-value pair argument ExpandOutput.
Data Types: double
Initial variance of the underlying asset, specified as a scalar numeric value.
Data Types: double
Long-term variance of the underlying asset, specified as a scalar numeric value.
Data Types: double
Mean revision speed for the underlying asset, specified as a scalar numeric value.
Data Types: double
Volatility of the variance of the underlying asset, specified as a scalar numeric value.
Data Types: double
Correlation between the Wiener processes for the underlying asset and its variance, specified as a scalar numeric value.
Data Types: double
Mean of the random percentage jump size (J), specified as a
scalar decimal value where log(1+J) is normally
distributed with mean
(log(1+MeanJ)-0.5*JumpVol^2)
and the standard deviation JumpVol.
Data Types: double
Standard deviation of log(1+J) where
J is the random percentage jump size, specified as a scalar
decimal value.
Data Types: double
Annual frequency of Poisson jump process, specified as a scalar numeric value.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: Price =
optByBatesNI(Rate,AssetPrice,Settle,Maturity,OptSpec,Strike,V0,ThetaV,Kappa,SigmaV,RhoSV,MeanJ,JumpVol,JumpFreq,'Basis',7)
Day-count of the instrument, specified as the comma-separated pair consisting of
'Basis' and a scalar using a supported value:
0 = actual/actual
1 = 30/360 (SIA)
2 = actual/360
3 = actual/365
4 = 30/360 (PSA)
5 = 30/360 (ISDA)
6 = 30/360 (European)
7 = actual/365 (Japanese)
8 = actual/actual (ICMA)
9 = actual/360 (ICMA)
10 = actual/365 (ICMA)
11 = 30/360E (ICMA)
12 = actual/365 (ISDA)
13 = BUS/252
For more information, see Basis.
Data Types: double
Continuously compounded underlying asset yield, specified as the comma-separated
pair consisting of 'DividendYield' and a scalar numeric
value.
Data Types: double
Volatility risk premium, specified as the comma-separated pair consisting of
'VolRiskPremium' and a scalar numeric value.
Data Types: double
Flag indicating "Little Heston Trap" formulation by Albrecher
et
al, specified as the comma-separated pair consisting of
'LittleTrap' and a logical:
true— Use the Albrecher et al formulation.false— Use the original Heston formation.
Data Types: logical
Absolute error tolerance for numerical integration, specified as the
comma-separated pair consisting of 'AbsTol' and a scalar numeric
value.
Data Types: double
Relative error tolerance for numerical integration, specified as the
comma-separated pair consisting of 'RelTol' and a scalar numeric
value.
Data Types: double
Numerical integration range used to approximate the continuous integral over
[0 Inf], specified as the comma-separated pair consisting of
'IntegrationRange' and a 1-by-2
vector representing [LowerLimit UpperLimit].
Data Types: double
Framework for computing option prices and sensitivities using numerical
integration of models, specified as the comma-separated pair consisting of
'Framework' and a scalar string or character vector with the
following values:
"heston1993"or'heston1993'— Method used in Heston (1993)"lewis2001"or'lewis2001'— Method used in Lewis (2001)
Data Types: char | string
Flag to expand the outputs, specified as the comma-separated pair consisting of
'ExpandOutput' and a logical:
true— Iftrue, the outputs areNRows-by-NColumnsmatrices.NRowsis the number of strikes for each column and it is determined by theStrikeinput. For example,Strikecan be aNRows-by-1vector, or aNRows-by-NColumnsmatrix.NColumnsis determined by the sizes ofAssetPrice,Settle,Maturity, andOptSpec, which must all be either scalar orNColumns-by-1vectors.false— Iffalse, the outputs areNINST-by-1vectors. Also, the inputsStrike,AssetPrice,Settle,Maturity, andOptSpecmust all be either scalar orNINST-by-1vectors.
Data Types: logical
Output Arguments
Option prices, returned as a NINST-by-1, or
NRows-by-NColumns, depending on
ExpandOutput.
More About
A vanilla option is a category of options that includes only the most standard components.
A vanilla option has an expiration date and straightforward strike price. American-style options and European-style options are both categorized as vanilla options.
The payoff for a vanilla option is as follows:
For a call:
For a put:
where:
St is the price of the underlying asset at time t.
K is the strike price.
For more information, see Vanilla Option.
The Bates model (Bates (1996)) is an extension of the Heston model, where, in addition to stochastic volatility, the jump diffusion parameters similar to Merton (1976) were also added to model sudden asset price movements.
The stochastic differential equation is:
where
r is the continuous risk-free rate.
q is the continuous dividend yield.
St is the asset price at time t.
vt is the asset price variance at time t.
J is the random percentage jump size conditional on the jump
occurring, where ln(1+J) is normally distributed with
mean and the standard deviation δ, and (1+J) has a lognormal distribution:
v0 is the initial variance of the asset price at t = 0 (v0> 0).
θ is the long-term variance level for (θ > 0).
κ is the mean reversion speed for (κ > 0).
σv is the volatility of variance for (σv > 0).
p is the correlation between the Wiener processes Wt and for (-1 ≤ p ≤ 1).
μJ is the mean of J for (μJ > -1).
δ is the standard deviation of
ln(1+J) for (δ ≥ 0).
is the annual frequency (intensity) of Poisson process Pt for ( ≥ 0).
The characteristic function for j = 1 (asset price mean measure) and j =2 (risk-neutral measure) is:
where
ϕ is the characteristic function variable.
ƛVolRisk is the volatility risk premium.
τ is the time to maturity for (τ = T - t).
i is the unit imaginary number for (i2= -1).
The definitions for Cj and Dj under “The Little Heston Trap” by Albrecher et al. (2007) are:
Numerical integration is used to evaluate the continuous integral for the inverse Fourier transform.
The numerical integration method under the Heston (1993) framework is based on the following expressions:
where
r is the continuous risk-free rate.
q is the continuous dividend yield.
St is the asset price at time t.
K is the strike.
τ is time to maturity (τ = T-t).
Call(K) is the call price at strike K.
Put(K) is the put price at strike K
i is a unit imaginary number (i2= -1)
ϕ is the characteristic function variable.
fj(ϕ) is the characteristic function for Pj(j = 1,2).
P1 is the probability of St > K under the asset price measure for the model.
P2 is the probability of St > K under the risk-neutral measure for the model.
Where j = 1,2 so that f1(ϕ) and f2(ϕ) are the characteristic functions for probabilities P1 and P2, respectively.
This framework is chosen with the default value “Heston1993” for the
Framework name-value pair argument.
Numerical integration is used to evaluate the continuous integral for the inverse Fourier transform.
The numerical integration method under the Lewis (2001) framework is based on the following expressions:
where
r is the continuous risk-free rate.
q is the continuous dividend yield.
St is the asset price at time t.
K is the strike.
τ is time to maturity (τ = T-t).
Call(K) is the call price at strike K.
Put(K) is the put price at strike K
i is a unit imaginary number (i2= -1)
ϕ is the characteristic function variable.
u is the characteristic function variable for integration, where .
f2(ϕ) is the characteristic function for P2.
P2 is the probability of St > K under the risk-neutral measure for the model.
This framework is chosen with the value “Lewis2001” for the
Framework name-value pair argument.
References
[1] Bates, D. S. “Jumps and Stochastic Volatility: Exchange Rate Processes Implicit in Deutsche Mark Options.” The Review of Financial Studies. Vol 9. No. 1. 1996.
[2] Heston, S. L. “A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options.” The Review of Financial Studies. Vol 6. No. 2. 1993.
[3] Lewis, A. L. “A Simple Option Formula for General Jump-Diffusion and Other Exponential Levy Processes.” Envision Financial Systems and OptionCity.net, 2001.
Version History
Introduced in R2018aAlthough optByBatesNI supports serial date numbers,
datetime values are recommended instead. The
datetime data type provides flexible date and time
formats, storage out to nanosecond precision, and properties to account for time
zones and daylight saving time.
To convert serial date numbers or text to datetime values, use the datetime function. For example:
t = datetime(738427.656845093,"ConvertFrom","datenum"); y = year(t)
y =
2021
There are no plans to remove support for serial date number inputs.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)