Minimización restringida mediante el uso del algoritmo genético
Este ejemplo muestra cómo minimizar una función objetivo sujeta a restricciones y límites de desigualdad no lineal utilizando el algoritmo genético.
Problema de minimización restringida
Para este problema, la función objetivo a minimizar es una función simple de una variable 2-D x.
simple_objective(x) = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;
Esta función se conoce como "leva", como se describe en L.C.W. Dixon y G.P. Szego [1].
Además, el problema tiene restricciones y límites no lineales.
x(1)*x(2) + x(1) - x(2) + 1.5 <= 0 (nonlinear constraint) 10 - x(1)*x(2) <= 0 (nonlinear constraint) 0 <= x(1) <= 1 (bound) 0 <= x(2) <= 13 (bound)
Codificar la función de aptitud
Cree un archivo MATLAB llamado simple_objective.m que contenga el siguiente código:
type simple_objectivefunction y = simple_objective(x) %SIMPLE_OBJECTIVE Objective function for PATTERNSEARCH solver % Copyright 2004 The MathWorks, Inc. x1 = x(1); x2 = x(2); y = (4-2.1.*x1.^2+x1.^4./3).*x1.^2+x1.*x2+(-4+4.*x2.^2).*x2.^2;
Los solucionadores como ga aceptan una única entrada x, donde x tiene tantos elementos como el número de variables en el problema. La función objetivo calcula el valor escalar de la función objetivo y lo devuelve en su único argumento de salida y.
Codificar la función de restricción
Cree un archivo MATLAB llamado simple_constraint.m que contenga el siguiente código:
type simple_constraintfunction [c, ceq] = simple_constraint(x)
%SIMPLE_CONSTRAINT Nonlinear inequality constraints.
% Copyright 2005-2007 The MathWorks, Inc.
c = [1.5 + x(1)*x(2) + x(1) - x(2);
-x(1)*x(2) + 10];
% No nonlinear equality constraints:
ceq = [];
La función de restricción calcula los valores de todas las restricciones de desigualdad e igualdad y devuelve los vectores c y ceq, respectivamente. El valor de c representa restricciones de desigualdad no lineal que el solucionador intenta hacer menores o iguales a cero. El valor de ceq representa restricciones de igualdad no lineales que el solucionador intenta hacer iguales a cero. Este ejemplo no tiene restricciones de igualdad no lineal, por lo tanto ceq = [] . Para obtener más detalles, consulte Restricciones no lineales.
Minimizar empleando ga
Especifique la función objetivo como un identificador de función.
ObjectiveFunction = @simple_objective;
Especifique los límites del problema.
lb = [0 0]; % Lower bounds ub = [1 13]; % Upper bounds
Especifique la función de restricción no lineal como un identificador de función.
ConstraintFunction = @simple_constraint;
Especifique el número de variables del problema.
nvars = 2;
Llame al solucionador, solicitando el punto óptimo x y el valor de la función en el punto óptimo fval.
rng default % For reproducibility [x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub,ConstraintFunction)
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
x = 1×2
0.8122 12.3103
fval = 9.1268e+04
Agregar visualización
Para observar el progreso del solucionador, especifique opciones que seleccionen dos funciones de gráfico. La función de gráfico gaplotbestf traza el mejor valor de la función objetivo en cada iteración, y la función de gráfico gaplotmaxconstr traza la máxima infracción de la restricción en cada iteración. Establezca estas dos funciones de gráfico en un arreglo de celdas. Además, muestre información sobre el progreso del solucionador en la ventana de comandos configurando la opción Display en 'iter'.
options = optimoptions("ga",'PlotFcn',{@gaplotbestf,@gaplotmaxconstr}, ... 'Display','iter');
Ejecute el solucionador, incluido el argumento options.
[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub, ...
ConstraintFunction,options)Single objective optimization:
2 Variables
2 Nonlinear inequality constraints
Options:
CreationFcn: @gacreationuniform
CrossoverFcn: @crossoverscattered
SelectionFcn: @selectionstochunif
MutationFcn: @mutationadaptfeasible
Best Max Stall
Generation Func-count f(x) Constraint Generations
1 2524 91986.8 7.796e-09 0
2 4986 94678.2 0 0
3 10362 96473.7 0 0
4 16243 91270.1 0.0009897 0
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.

x = 1×2
0.8123 12.3104
fval = 9.1270e+04
Con visualización iterativa, ga proporciona detalles sobre el tipo de problema y los operadores de creación, cruce, mutación y selección.
Las restricciones no lineales hacen que ga resuelva muchos subproblemas en cada iteración. Como se muestra en los gráficos y en la visualización iterativa, el proceso de solución tiene pocas iteraciones. Sin embargo, la columna Func-count en la visualización iterativa muestra muchas evaluaciones de funciones por iteración.
El solucionador ga maneja las restricciones y límites lineales de manera diferente a las restricciones no lineales. Todas las restricciones y límites lineales se satisfacen durante toda la optimización. Sin embargo, ga puede no satisfacer todas las restricciones no lineales en cada generación. Si ga converge a una solución, las restricciones no lineales se satisfarán en esa solución.
ga utiliza las funciones de mutación y cruce para producir nuevos individuos en cada generación. La forma en que ga satisface las restricciones lineales y de límites es utilizando funciones de mutación y cruce que solo generan puntos factibles. Por ejemplo, en la llamada anterior a ga, la función de mutación predeterminada (para problemas sin restricciones) mutationgaussian no satisface las restricciones lineales y, por lo tanto, ga utiliza la función mutationadaptfeasible en su lugar de manera predeterminada. Si proporciona una función de mutación personalizada, esta función personalizada solo debe generar puntos que sean factibles con respecto a las restricciones lineales y de límites. Todas las funciones de cruce en la toolbox generan puntos que satisfacen las restricciones y límites lineales.
Sin embargo, cuando su problema contiene restricciones de números enteros, ga exige que todas las iteraciones satisfagan límites y restricciones lineales. Esta viabilidad se produce para todos los operadores de mutación, cruce y creación, dentro de una pequeña tolerancia.
Proporcionar un punto de partida
Para acelerar el solucionador, puede proporcionar una población inicial en la opción InitialPopulationMatrix. ga utiliza la población inicial para iniciar su optimización. Especifique un vector de fila o una matriz donde cada fila representa un punto de inicio.
X0 = [0.8 12.5]; % Start point (row vector) options.InitialPopulationMatrix = X0; [x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],lb,ub, ... ConstraintFunction,options)
Single objective optimization:
2 Variables
2 Nonlinear inequality constraints
Options:
CreationFcn: @gacreationuniform
CrossoverFcn: @crossoverscattered
SelectionFcn: @selectionstochunif
MutationFcn: @mutationadaptfeasible
Best Max Stall
Generation Func-count f(x) Constraint Generations
1 2500 91769.6 0 0
2 4962 97536.4 0 0
3 7412 91268.4 0.00098 0
4 9862 91268.1 0.0009893 0
5 12312 91267.9 0.0009943 0
Optimization finished: average change in the fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
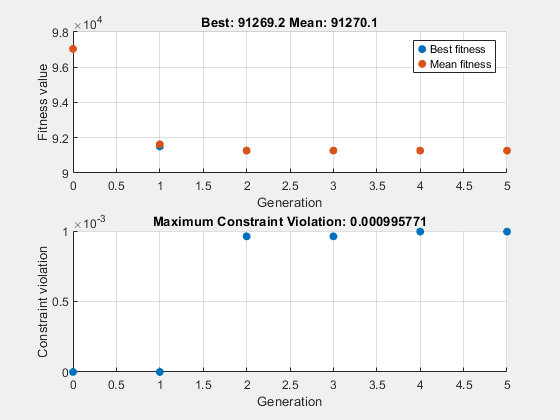
x = 1×2
0.8122 12.3103
fval = 9.1268e+04
En este caso, proporcionar un punto de inicio no cambia sustancialmente el progreso del solucionador.
Referencias
[1] Dixon, L. C. W., y G .P. Szego (eds.). Hacia la optimización global 2 Holanda del Norte: Elsevier Science Ltd., Ámsterdam, 1978.