Esta página se ha traducido mediante traducción automática. Haga clic aquí para ver la última versión en inglés.

Codificación y minimización de una función de aptitud mediante el algoritmo genético

Abrir script en vivo

Este ejemplo muestra cómo crear y minimizar una función de aptitud para el solucionador de algoritmo genético ga utilizando tres técnicas:

  • Básico

  • Incluir parámetros adicionales

  • Vectorizado para mayor velocidad

Función básica de la aptitud

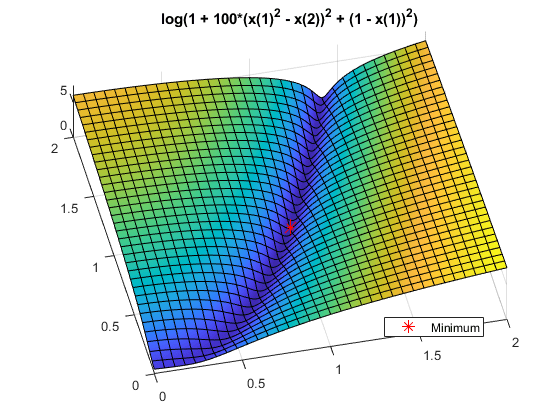
La función de aptitud básica es la función de Rosenbrock, una función de prueba común para optimizadores. La función es una suma de cuadrados:

f(x)=100(x12-x2)2+(1-x1)2.

La función tiene un valor mínimo de cero en el punto [1,1]. Como la función de Rosenbrock es bastante pronunciada, grafique el logaritmo de uno más la función.

fsurf(@(x,y)log(1 + 100*(x.^2 - y).^2 + (1 - x).^2),[0,2])
title('log(1 + 100*(x(1)^2 - x(2))^2 + (1 - x(1))^2)')
view(-13,78)
hold on
h1 = plot3(1,1,0.1,'r*','MarkerSize',12);
legend(h1,'Minimum','Location','best');
hold off

Código de función de aptitud

El archivo de función simple_fitness implementa la función de Rosenbrock.

type simple_fitness
function y = simple_fitness(x)
%SIMPLE_FITNESS fitness function for GA

%   Copyright 2004 The MathWorks, Inc. 

  y = 100 * (x(1)^2 - x(2)) ^2 + (1 - x(1))^2;

Una función de aptitud debe tomar una entrada x donde x es un vector de fila con tantos elementos como el número de variables en el problema. La función de aptitud calcula el valor de la función y devuelve ese valor escalar en su único argumento de retorno y.

Minimizar el uso de ga

Para minimizar la función de aptitud usando ga, pase un identificador de función a la función de aptitud así como también el número de variables en el problema. Para que ga examine la región relevante, incluya los límites -3 <= x(i) <= 3. Pase los límites como quinto y sexto argumento después de numberOfVariables. Para obtener detalles sobre la sintaxis de ga, consulte ga.

ga es un algoritmo aleatorio. Para lograr reproducibilidad, configure el flujo de números aleatorios.

rng default % For reproducibility
FitnessFunction = @simple_fitness;
numberOfVariables = 2;
lb = [-3,-3];
ub = [3,3];
[x,fval] = ga(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub)
Optimization terminated: maximum number of generations exceeded.

x = 1×2

    1.5083    2.2781


fval = 0.2594

El x devuelto por el solucionador es el mejor punto en la población final calculada por ga. fval es el valor de la función simple_fitness evaluada en el punto x. ga no encontró una solución especialmente buena. Para conocer formas de mejorar la solución, consulte Efectos de las opciones de algoritmos genéticos.

Función de aptitud con parámetros adicionales

A veces, su función de aptitud tiene parámetros adicionales que actúan como constantes durante la optimización. Por ejemplo, una función de Rosenbrock generalizada puede tener parámetros adicionales que representan las constantes 100 y 1:

f(x,a,b)=a(x12-x2)2+(b-x1)2.

a y b son parámetros de la función de aptitud que actúan como constantes durante la optimización (no varían como parte de la minimización). El archivo parameterized_fitness.m implementa esta función de aptitud parametrizada.

type parameterized_fitness
function y = parameterized_fitness(x,p1,p2)
%PARAMETERIZED_FITNESS fitness function for GA

%   Copyright 2004 The MathWorks, Inc.        
 
y = p1 * (x(1)^2 - x(2)) ^2 + (p2 - x(1))^2;

Minimizar el uso de parámetros adicionales

Utilice una función anónima para capturar los valores de los argumentos adicionales, es decir, las constantes a y b. Crea un identificador de función FitnessFunction para una función anónima que toma una entrada x y llama a parameterized_fitness con x, a y b. La función anónima contiene los valores de a y b que existen cuando se crea el identificador de función.

a = 100;
b = 1; % define constant values
FitnessFunction = @(x) parameterized_fitness(x,a,b);
[x,fval] = ga(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub)
Optimization terminated: maximum number of generations exceeded.

x = 1×2

    1.3198    1.7434


fval = 0.1025

Consulte Pasar parámetros adicionales.

Función de aptitud vectorizada

Para ganar velocidad, vectorice su función de aptitud. Una función de aptitud vectorizada calcula la aptitud de una colección de puntos a la vez, lo que generalmente ahorra tiempo en comparación con la evaluación de estos puntos individualmente. Para escribir una función de aptitud vectorizada, haga que su función acepte una matriz, donde cada fila de la matriz representa un punto, y haga que la función de aptitud devuelva un vector de columna de valores de la función de aptitud.

Para cambiar el archivo de función parameterized_fitness a una forma vectorizada:

  • Cambie cada variable x(i) a x(:,i), es decir, el vector de columna de variables correspondiente a x(i).

  • Cambie cada multiplicación vectorial * a .* y cada exponenciación ^ a .^ indicando que las operaciones son elemento por elemento. No hay multiplicaciones vectoriales en este código, así que simplemente cambie los exponentes.

type vectorized_fitness
function y = vectorized_fitness(x,p1,p2)
%VECTORIZED_FITNESS fitness function for GA

%   Copyright 2004-2010 The MathWorks, Inc.  

y = p1 * (x(:,1).^2 - x(:,2)).^2 + (p2 - x(:,1)).^2;

Esta versión vectorizada de la función de aptitud toma una matriz x con una cantidad arbitraria de puntos, es decir, una cantidad arbitraria de filas, y devuelve un vector de columna y con la misma cantidad de filas que x.

Indique al solucionador que la función de aptitud está vectorizada en la opción 'UseVectorized'.

options = optimoptions(@ga,'UseVectorized',true);

Incluir opciones como último argumento de ga.

VFitnessFunction = @(x) vectorized_fitness(x,100,1);
[x,fval] = ga(VFitnessFunction,numberOfVariables,[],[],[],[],lb,ub,[],options)
Optimization terminated: maximum number of generations exceeded.

x = 1×2

    1.6219    2.6334


fval = 0.3876

¿Cuál es la diferencia de velocidad? Cronometrar la optimización tanto con como sin vectorización.

tic
[x,fval] = ga(VFitnessFunction,numberOfVariables,[],[],[],[],lb,ub,[],options);
Optimization terminated: maximum number of generations exceeded.

v = toc;
tic
[x,fval] = ga(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub);
Optimization terminated: maximum number of generations exceeded.

nv = toc;
fprintf('Using vectorization took %f seconds. No vectorization took %f seconds.\n',v,nv)
Using vectorization took 0.153337 seconds. No vectorization took 0.212880 seconds.

En este caso, la mejora por vectorización no fue grande, porque calcular la función de aptitud toma muy poco tiempo. Sin embargo, para funciones de aptitud que consumen más tiempo, la vectorización puede ser útil. Consulte Vectorize the Fitness Function.

Consulte también

Temas