crossfix
Intersection points for pairs of great circles or small circles
Syntax
Description
[
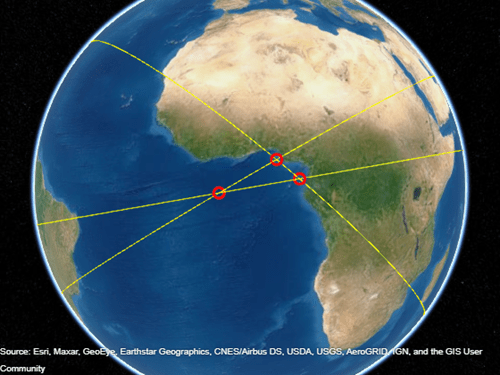
finds the intersection points of pairs of great circles. Define each great circle by
specifying the latitude latIntersect,lonIntersect] = crossfix(lat,lon,az)lat and longitude lon of a
point on the circle and the azimuth az at that point.
[
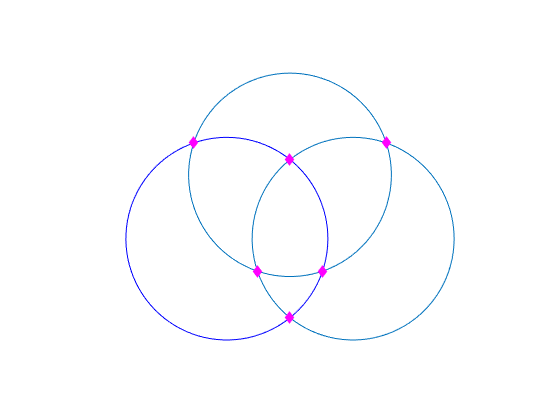
enables you to find the intersection points of great circles and small circles. When an
element of latIntersect,lonIntersect] = crossfix(lat,lon,az_radius,ind)ind is 0, the corresponding elements of
lat and lon define the center of a small circle,
and az_radius specifies the radius of the small circle. When an element
of ind is 1, the corresponding element of
lat and lon define a point on a great circle,
and az_radius specifies the azimuth.
[
finds the intersection point closest to the point specified by
latIntersect,lonIntersect] = crossfix(lat,lon,az_radius,ind,latEstimate,lonEstimate)latEstimate and lonEstimate.
[
specifies the angle units for the coordinates, azimuth, and radii, in addition to any
combination of input arguments from the previous syntaxes.latIntersect,lonIntersect] = crossfix(___,units)
mat = crossfix(___)mat.
Examples
Input Arguments
Output Arguments
Tips
To find intersection points by using rhumb line azimuths and nautical mile distances, use the
navfixfunction.
Version History
Introduced before R2006a