symrcm

Sparse reverse Cuthill-McKee ordering

Syntax

r = symrcm(S)


Description

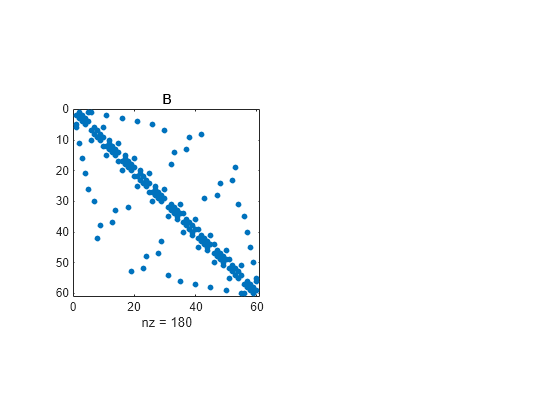
r = symrcm(S) returns the symmetric reverse Cuthill-McKee ordering of S. This is a permutation r such that S(r,r) tends to have its nonzero elements closer to the diagonal. This is a good preordering for LU or Cholesky factorization of matrices that come from long, skinny problems. The ordering works for both symmetric and nonsymmetric S.

For a real, symmetric sparse matrix, S, the eigenvalues of S(r,r) are the same as those of S, but eig(S(r,r)) probably takes less time to compute than eig(S).

Examples

Reverse Cuthill-McKee Ordering

The statement

B = bucky;

uses a function in the demos toolbox to generate the adjacency graph of a truncated icosahedron. This is better known as a soccer ball, a Buckminster Fuller geodesic dome (hence the name bucky), or, more recently, as a 60-atom carbon molecule. There are 60 vertices. The vertices have been ordered by numbering half of them from one hemisphere, pentagon by pentagon; then reflecting into the other hemisphere and gluing the two halves together.

With this numbering, the matrix does not have a particularly narrow bandwidth, as the first spy plot shows:

figure();
subplot(1,2,1),spy(B),title('B')

The reverse Cuthill-McKee ordering is obtained with:

p = symrcm(B);
R = B(p,p);

The spy plot shows a much narrower bandwidth.

subplot(1,2,2),spy(R),title('B(p,p)')

This example is continued in the reference page for symamd.

The bandwidth can also be computed with:

[i,j] = find(B);
bw = max(i-j) + 1;

The bandwidths of B and R are 35 and 12, respectively.

Algorithms

The algorithm first finds a pseudoperipheral vertex of the graph of the matrix. It then generates a level structure by breadth-first search and orders the vertices by decreasing distance from the pseudoperipheral vertex. The implementation is based closely on the SPARSPAK implementation described by George and Liu.

References

[1] George, Alan and Joseph Liu, Computer Solution of Large Sparse Positive Definite Systems, Prentice-Hall, 1981.

[2] Gilbert, John R., Cleve Moler, and Robert Schreiber, “Sparse Matrices in MATLAB: Design and Implementation,” SIAM Journal on Matrix Analysis, 1992. A slightly expanded version is also available as a technical report from the Xerox Palo Alto Research Center.

Extended Capabilities

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

Version History

Introduced before R2006a