Calcular gradientes y matrices hessianas con Symbolic Math Toolbox
Este ejemplo muestra cómo obtener soluciones más rápidas y robustas para problemas de optimización no lineales con fmincon y las funciones de Symbolic Math Toolbox™. Si tiene una licencia de Symbolic Math Toolbox, puede calcular de forma fácil gradientes analíticos y matrices hessianas de funciones objetivo y de restricción usando las funciones de Symbolic Math Toolbox siguientes:
jacobian(Symbolic Math Toolbox) genera el gradiente de una función escalar y una matriz de las derivadas parciales de una función de vector. De manera que, por ejemplo, puede obtener la matriz hessiana (las segundas derivadas de la función objetivo) aplicandojacobianal gradiente. Este ejemplo muestra cómo utilizarjacobianpara generar gradientes simbólicos y matrices hessianas de funciones objetivo y de restricción.matlabFunction(Symbolic Math Toolbox) genera una función anónima o un archivo que calcula el valor de una expresión simbólica. Este ejemplo muestra cómo utilizarmatlabFunctionpara generar archivos que evalúen las funciones objetivo y de restricción y sus derivadas en puntos arbitrarios.
Las funciones de Symbolic Math Toolbox tienen sintaxis y estructuras diferentes en comparación con las funciones de Optimization Toolbox™. En particular, las variables simbólicas son escalares reales o complejas, mientras que las funciones de Optimization Toolbox pasan argumentos de vector. Por lo tanto, necesita dar varios pasos para generar de forma simbólica la función objetivo, de restricción o todas sus derivadas requeridas, en una forma adecuada para el algoritmo interior-point de fmincon.
La optimización basada en problemas puede calcular y utilizar gradientes de forma automática. Consulte Automatic Differentiation in Optimization Toolbox. Si desea ver un enfoque basado en problemas de este problema usando la diferenciación automática, consulte Constrained Electrostatic Nonlinear Optimization Using Optimization Variables.
Descripción del problema
Considere el problema de electroestática de colocar 10 electrones en un cuerpo conductor. Los electrones se organizan de una forma que minimiza su energía potencial total, sujeta a la restricción de encontrarse en el interior del cuerpo. Todos los electrones están en el límite del cuerpo en un mínimo. Los electrones son indistinguibles, así que no existe un mínimo único para este problema (permutando los electrones en una solución se obtiene otra solución válida). Este ejemplo está inspirado en Dolan, Moré y Munson [58].
Este ejemplo es un cuerpo conductor definido por las desigualdades
.
Este cuerpo parece una pirámide sobre un esfera.
[X,Y] = meshgrid(-1:.01:1); Z1 = -abs(X) - abs(Y); Z2 = -1 - sqrt(1 - X.^2 - Y.^2); Z2 = real(Z2); W1 = Z1; W2 = Z2; W1(Z1 < Z2) = nan; % Only plot points where Z1 > Z2 W2(Z1 < Z2) = nan; % Only plot points where Z1 > Z2 hand = figure; % Handle to the figure, for more plotting later set(gcf,'Color','w') % White background surf(X,Y,W1,'LineStyle','none'); hold on surf(X,Y,W2,'LineStyle','none'); view(-44,18)
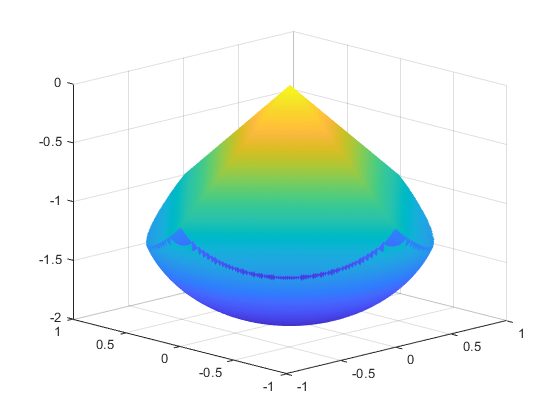
Existe un ligero hueco entre las superficies superior e inferior de la figura. Dicho hueco es un artefacto de la rutina de representación general que se utiliza para crear la figura. La rutina borra cualquier parche rectangular en una superficie que está en contacto con la otra superficie.
Crear variables
Genere un vector simbólico x como un vector de 30 por 1 compuesto de variables simbólicas reales xij, estando i entre 1 y 10 y j, entre 1 y 3. Estas variables representan las tres coordenadas del electrón i: xi1 corresponde a la coordenada , xi2 corresponde a la coordenada y xi3 corresponde a la coordenada .
x = cell(3, 10); for i = 1:10 for j = 1:3 x{j,i} = sprintf('x%d%d',i,j); end end x = x(:); % Now x is a 30-by-1 vector x = sym(x, 'real');
Muestre el vector x.
x
x =
Incluir restricciones lineales
Escriba las restricciones lineales
como un conjunto de cuatro desigualdades lineales por cada electrón:
xi3 - xi1 - xi2 ≤ 0 xi3 - xi1 + xi2 ≤ 0 xi3 + xi1 - xi2 ≤ 0 xi3 + xi1 + xi2 ≤ 0
Por lo tanto, este problema tiene un total de 40 desigualdades lineales.
Escriba las desigualdades de una forma estructurada.
B = [1,1,1;-1,1,1;1,-1,1;-1,-1,1]; A = zeros(40,30); for i=1:10 A(4*i-3:4*i,3*i-2:3*i) = B; end b = zeros(40,1);
Puede observar que A*x ≤ b representa las desigualdades.
disp(A*x)
Crear las restricciones no lineales y sus gradientes y matrices hessianas
Las restricciones no lineales también están estructuradas.
.
Genere las restricciones y sus gradientes y matrices hessianas.
c = sym(zeros(1,10)); i = 1:10; c = (x(3*i-2).^2 + x(3*i-1).^2 + (x(3*i)+1).^2 - 1).'; gradc = jacobian(c,x).'; % .' performs transpose hessc = cell(1, 10); for i = 1:10 hessc{i} = jacobian(gradc(:,i),x); end
El vector de restricción c es un vector fila y el gradiente de c(i) se representa en la columna i-ésima de la matriz gradc. Esta forma es correcta, según se describe en Restricciones no lineales.
Las matrices hessianas, hessc{1}, ..., hessc{10}, son cuadradas y simétricas. Este ejemplo las almacena en un arreglo de celdas, que es mejor que almacenarlas en variables separadas como hessc1, ..., hessc10.
Utilice la sintaxis .' para trasponer. La sintaxis ' hace referencia a la trasposición conjugada, que tiene derivadas simbólicas diferentes.
Crear la función objetivo y su gradiente y matriz hessiana
La función objetivo, la energía potencial, es la suma de las inversas de las distancias entre cada par de electrones.
.
La distancia es la raíz cuadrada de la suma de los cuadrados de las diferencias en los componentes de los vectores.
Calcule la energía (función objetivo) y su gradiente y matriz hessiana.
energy = sym(0); for i = 1:3:25 for j = i+3:3:28 dist = x(i:i+2) - x(j:j+2); energy = energy + 1/sqrt(dist.'*dist); end end gradenergy = jacobian(energy,x).'; hessenergy = jacobian(gradenergy,x);
Crear el archivo de la función objetivo
La función objetivo tiene dos salidas, energy y gradenergy. Ponga ambas funciones en un vector cuando llame a matlabFunction para reducir el número de subexpresiones que matlabFunction genera y devolver el gradiente solo cuando la función de llamada (fmincon, en este caso) solicite ambas salidas. Puede colocar los archivos resultantes en cualquier carpeta de la ruta de MATLAB. En este caso, colóquelos en su carpeta actual.
currdir = [pwd filesep]; % You might need to use currdir = pwd filename = [currdir,'demoenergy.m']; matlabFunction(energy,gradenergy,'file',filename,'vars',{x});
matlabFunction devuelve energy como la primera salida y gradenergy como la segunda. La función también toma un vector de única entrada {x} en vez de una lista de entradas x11, ..., x103.
El archivo resultante demoenergy.m contiene las líneas siguientes u otras similares:
function [energy,gradenergy] = demoenergy(in1) %DEMOENERGY % [ENERGY,GRADENERGY] = DEMOENERGY(IN1) ... x101 = in1(28,:); ... energy = 1./t140.^(1./2) + ...; if nargout > 1 ... gradenergy = [(t174.*(t185 - 2.*x11))./2 - ...]; end
Esta función tiene la forma correcta para una función objetivo con un gradiente. Consulte Escribir funciones objetivo escalares.
Crear el archivo de la función de restricción
Genere la función de restricción no lineal y póngala en el formato correcto.
filename = [currdir,'democonstr.m']; matlabFunction(c,[],gradc,[],'file',filename,'vars',{x},... 'outputs',{'c','ceq','gradc','gradceq'});
El archivo resultante democonstr.m contiene las líneas siguientes u otras similares:
function [c,ceq,gradc,gradceq] = democonstr(in1) %DEMOCONSTR % [C,CEQ,GRADC,GRADCEQ] = DEMOCONSTR(IN1) ... x101 = in1(28,:); ... c = [t417.^2 + ...]; if nargout > 1 ceq = []; end if nargout > 2 gradc = [2.*x11,...]; end if nargout > 3 gradceq = []; end
Esta función tiene la forma correcta para una función de restricción con un gradiente. Consulte Restricciones no lineales.
Generar los archivos de la matriz hessiana
Para generar la matriz hessiana del lagrangiano del problema, primero tiene que generar los archivos para la matriz hessiana de energía y las matrices hessianas de restricción.
La matriz hessiana de la función objetivo, hessenergy, es una expresión simbólica grande que contiene alrededor de 150.000 símbolos, como se muestra evaluando size(char(hessenergy)). Así, ejecutar matlabFunction(hessenergy) lleva una cantidad de tiempo sustancial.
Genere el archivo hessenergy.m.
filename = [currdir,'hessenergy.m']; matlabFunction(hessenergy,'file',filename,'vars',{x});
En contraste, las matrices hessianas de las funciones de restricción son pequeñas y rápidas de calcular.
for i = 1:10 ii = num2str(i); thename = ['hessc',ii]; filename = [currdir,thename,'.m']; matlabFunction(hessc{i},'file',filename,'vars',{x}); end
Después de generar todos los archivos para el objetivo y las restricciones, póngalos juntos con los multiplicadores lagrangianos apropiados en la función auxiliar hessfinal.m, cuyo código aparece al final de este ejemplo.
Ejecutar la optimización
Inicie la optimización con los electrones distribuidos de forma aleatoria en una esfera de radio 1/2 centrada en [0,0,–1].
rng default % For reproducibility Xinitial = randn(3,10); % Columns are normal 3-D vectors for j=1:10 Xinitial(:,j) = Xinitial(:,j)/norm(Xinitial(:,j))/2; % This normalizes to a 1/2-sphere end Xinitial(3,:) = Xinitial(3,:) - 1; % Center at [0,0,-1] Xinitial = Xinitial(:); % Convert to a column vector
Establezca opciones para utilizar el algoritmo interior-point y para utilizar gradientes y la matriz hessiana.
options = optimoptions(@fmincon,'Algorithm','interior-point','SpecifyObjectiveGradient',true,... 'SpecifyConstraintGradient',true,'HessianFcn',@hessfinal,'Display','final');
Llame a fmincon.
[xfinal,fval,exitflag,output] = fmincon(@demoenergy,Xinitial,...
A,b,[],[],[],[],@democonstr,options);Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
Examine el valor de la función objetivo, el indicador de salida, el número de iteraciones y el número de evaluaciones de función.
disp(fval)
34.1365
disp(exitflag)
1
disp(output.iterations)
19
disp(output.funcCount)
28
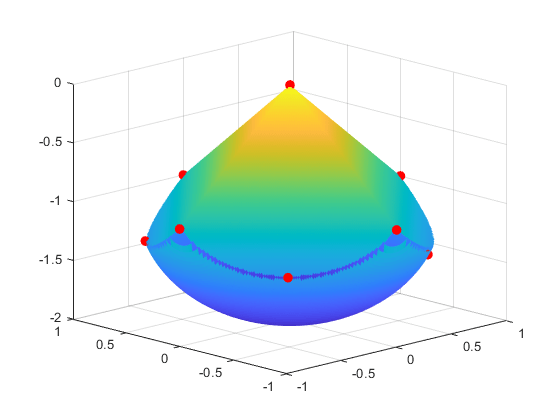
Incluso si las posiciones iniciales de los electrones son aleatorias, las posiciones finales son más simétricas.
for i = 1:10 plot3(xfinal(3*i-2),xfinal(3*i-1),xfinal(3*i),'r.','MarkerSize',25); end
Para examinar la geometría 3D entera, gire la figura.
rotate3d
figure(hand)
Comparación con la optimización sin gradientes ni matrices hessianas
El uso de gradientes y matrices hessianas hace que la optimización funcione de forma más rápida y precisa. Para comparar la misma optimización sin utilizar información del gradiente o la matriz hessiana, establezca las opciones para no utilizarlos.
options = optimoptions(@fmincon,'Algorithm','interior-point',... 'Display','final'); [xfinal2,fval2,exitflag2,output2] = fmincon(@demoenergy,Xinitial,... A,b,[],[],[],[],@democonstr,options);
Feasible point with lower objective function value found. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
Examine el valor de la función objetivo, el indicador de salida, el número de iteraciones y el número de evaluaciones de función.
disp(fval2)
34.1365
disp(exitflag2)
1
disp(output2.iterations)
77
disp(output2.funcCount)
2434
Compare el número de iteraciones y el número de evaluaciones de función con y sin información de derivadas.
tbl = table([output.iterations;output2.iterations],[output.funcCount;output2.funcCount],... 'RowNames',{'With Derivatives','Without Derivatives'},'VariableNames',{'Iterations','Fevals'})
tbl=2×2 table
Iterations Fevals
__________ ______
With Derivatives 19 28
Without Derivatives 77 2434
Borrar los supuestos de variables simbólicas
Las variables simbólicas de este ejemplo tienen el supuesto de que son reales en el espacio de trabajo del motor simbólico. Eliminar las variables no borra este supuesto del espacio de trabajo del motor simbólico. Borre los supuestos de variables utilizando syms.
syms xVerifique que los supuestos están vacíos.
assumptions(x)
ans = Empty sym: 1-by-0
Función auxiliar
El siguiente código crea la función auxiliar hessfinal.
function H = hessfinal(X,lambda) % % Call the function hessenergy to start H = hessenergy(X); % Add the Lagrange multipliers * the constraint Hessians H = H + hessc1(X) * lambda.ineqnonlin(1); H = H + hessc2(X) * lambda.ineqnonlin(2); H = H + hessc3(X) * lambda.ineqnonlin(3); H = H + hessc4(X) * lambda.ineqnonlin(4); H = H + hessc5(X) * lambda.ineqnonlin(5); H = H + hessc6(X) * lambda.ineqnonlin(6); H = H + hessc7(X) * lambda.ineqnonlin(7); H = H + hessc8(X) * lambda.ineqnonlin(8); H = H + hessc9(X) * lambda.ineqnonlin(9); H = H + hessc10(X) * lambda.ineqnonlin(10); end