Algoritmos de optimización no lineal sin restricciones
Definición de la optimización sin restricciones
La minimización sin restricciones es el problema de encontrar un vector x que es un mínimo local de una función escalar f(x):
El concepto sin restricciones significa que no se coloca ninguna restricción en el rango de x.
Algoritmo trust-region de fminunc
Métodos trust-region para la minimización no lineal
Muchos de los métodos utilizados en los solvers de Optimization Toolbox™ se basan en regiones de confianza, un concepto sencillo, pero potente de optimización.
Para comprender el enfoque trust-region de la optimización, considere el problema de minimización no restringida, minimice f(x), donde la función toma argumentos de vector y devuelve escalares. Suponga que está en un punto x en el espacio n y desea mejorar, es decir, moverse a un punto con un valor de función inferior. La idea básica es aproximar f con una función más sencilla q, que refleja razonablemente el comportamiento de la función f en un entorno N alrededor del punto x. Este entorno es la región de confianza. Se calcula un paso de prueba s minimizando (o minimizando aproximadamente) en N. Este es el subproblema trust-region,
| (1) |
El punto actual se actualiza para ser x + s si f(x + s) < f(x); de lo contrario, el punto actual permanece sin cambiar y N, la región de confianza, disminuye y se repite el cálculo del paso de prueba.
Las principales cuestiones al definir un enfoque específico trust-region para minimizar f(x) son cómo elegir y calcular la aproximación q (definida en el punto actual x), cómo elegir y modificar la región de confianza N y cómo resolver de forma precisa el subproblema trust-region. Esta sección se centra en el problema no restringido. En secciones posteriores, se abordan otras complicaciones causadas por la presencia de restricciones en las variables.
En el método estándar trust-region ([48]), la aproximación cuadrática q se define por los dos primeros términos de la aproximación de Taylor a F en x; el entorno N suele tener forma de esfera o de elipsoide. En términos matemáticos, el subproblema trust-region se indica, por lo general, como
| (2) |
donde g es el gradiente de f en el punto actual x, H es la matriz hessiana (la matriz simétrica de segundas derivadas), D es una matriz de escalado diagonal, Δ es un escalar positivo y ‖ . ‖ es la norma euclídea. Existen buenos algoritmos para resolver Ecuación 2 (consulte [48]); estos algoritmos incluyen, por lo general, el cálculo de todos los valores propios de H y un proceso de Newton aplicado a la ecuación secular
Estos algoritmos proporcionan una solución precisa para Ecuación 2. Sin embargo, requieren tiempo proporcional a varias factorizaciones de H. Por lo tanto, para los problemas a gran escala se necesita un enfoque diferente. Varias estrategias heurísticas y de aproximación, basadas en Ecuación 2, se han propuesto en la literatura ([42] y [50]). El enfoque de aproximación seguido en los solvers de Optimization Toolbox es restringir el subproblema trust-region a un subespacio bidimensional S ([39] y [42]). Una vez calculado el subespacio S, el trabajo para resolver Ecuación 2 es trivial incluso si se necesita información completa del valor propio/vector propio (ya que, en el subespacio, el problema solo es bidimensional). El trabajo dominante se ha desplazado ahora a la determinación del subespacio.
El subespacio bidimensional S se determina con la ayuda de un proceso de gradiente conjugado precondicionado descrito a continuación. El solver define S como el espacio lineal que abarcan s1 y s2, donde s1 está en la dirección del gradiente g y s2 es una dirección de Newton aproximada, es decir, una solución para
| (3) |
o una dirección de curvatura negativa,
| (4) |
La filosofía sobre la que se basa esta elección de S es forzar la convergencia global (mediante la dirección de descenso más pronunciado o la dirección de curvatura negativa) y lograr una convergencia local rápida (mediante el paso de Newton, cuando exista).
Ahora es fácil dar una aproximación de minimización no restringida utilizando ideas trust-region:
Formule el subproblema trust-region bidimensional.
Resuelva Ecuación 2 para determinar el paso de prueba s.
Si f(x + s) < f(x), entonces x = x + s.
Ajuste Δ.
Estos cuatro pasos se repiten hasta la convergencia. La dimensión Δ de la región de confianza se ajusta de acuerdo con las reglas estándar. En particular, disminuye si el paso de prueba no se acepta, es decir, f(x + s) ≥ f(x). Consulte [46] y [49] para ver una exposición sobre este aspecto.
Los solvers de Optimization Toolbox tratan unos pocos casos importantes especiales de f con funciones especializadas: mínimos cuadrados no lineales, funciones cuadráticas y mínimos cuadrados lineales. Sin embargo, las ideas algorítmicas subyacentes son las mismas que para el caso general. Estos casos especiales se abordarán en secciones posteriores.
Método del gradiente conjugado precondicionado
Una forma popular de resolver sistemas definidos grandes, simétricos y positivos de ecuaciones lineales Hp = –g es el método de los gradientes conjugados precondicionados (PCG). Este enfoque iterativo requiere la capacidad de calcular productos de matriz-vector de la forma H·v, donde v es un vector arbitrario. La matriz definida simétrica positiva M es un precondicionador para H. Es decir, M = C2, donde C–1HC–1 es una matriz bien condicionada o una matriz con valores propios agrupados.
En un contexto de minimización, puede dar por supuesto que la matriz hessiana H es simétrica. Sin embargo, está garantizado que H solo sea definida positiva en el entorno de un minimizador fuerte. El algoritmo PCG existe cuando encuentra una dirección de curvatura negativa (o cero), es decir, dTHd ≤ 0. La dirección de salida PCG p es una dirección de curvatura negativa o una solución aproximada al sistema de Newton Hp = –g. En cualquier caso, p ayuda a definir el subespacio bidimensional utilizado en el enfoque trust-region abordado en Métodos trust-region para la minimización no lineal.
Algoritmo quasi-newton de fminunc
Conceptos básicos de la optimización sin restricciones
Aunque existe un amplio espectro de métodos para la optimización sin restricciones, estos se pueden clasificar en términos generales en función de la información de las derivadas que se utilice o no. Buscar métodos que solo utilicen evaluaciones de función (por ejemplo, la búsqueda simplex de Nelder y Mead [30]) es más adecuado para problemas que no son suaves o que tienen una serie de discontinuidades. Los métodos de gradiente son, de forma general, más eficientes cuando la función que debe minimizarse es continua en su primera derivada. Los métodos de orden más alto, como el método de Newton, solo son verdaderamente adecuados cuando la información de segundo orden se calcula fácil y rápidamente, ya que el cálculo de la información de segundo orden, mediante diferenciación numérica, es computacionalmente caro.
Los métodos de gradiente utilizan información sobre la pendiente de la función para dictar una dirección de búsqueda en la que se cree que está el mínimo. El más simple de estos métodos es el del descenso más pronunciado, en el que se ejecuta una búsqueda en una dirección, –∇f(x), donde ∇f(x) es el gradiente de la función objetivo. Este método es muy ineficiente cuando la función que debe minimizarse cuenta con valles largos y estrechos, por ejemplo, en el caso de la función de Rosenbrock
| (5) |
El mínimo de esta función está en x = [1,1], donde f(x) = 0. En la figura inferior se muestra un mapa de contorno de esta función, junto con la ruta de solución del mínimo para una implementación del descenso más pronunciado que empieza en el punto [-1.9,2]. La optimización se terminó después de 1000 iteraciones, que sigue siendo una distancia considerable desde el mínimo. Las áreas en negro indican el lugar en que el método zigzaguea continuamente de un lado al otro del valle. Tenga en cuenta que hacia el centro de la representación se dan varios pasos más grandes cuando un punto cae exactamente en el centro del valle.
Figura 5-1, Método del descenso más pronunciado en la función de Rosenbrock

Esta función, también conocida como función del plátano, es conocida en ejemplos sin restricciones por la forma en la que la curvatura se dobla alrededor del origen. La función de Rosenbrock se utiliza a lo largo de esta sección para ilustrar el uso de una variedad de técnicas de optimización. Los contornos se han representado en incrementos exponenciales debido a la inclinación de la ladera que rodea el valle en forma de U.
Para una descripción completa de esta figura, incluidos los scripts que generan los puntos iterativos, consulte Minimización de la función banana.
Métodos quasi-Newton
De los métodos que utilizan información de gradiente, los preferidos son los métodos quasi-Newton. Estos métodos acumulan información de la curvatura en cada iteración para formular un problema de modelo cuadrático de la forma
| (6) |
donde la matriz hessiana, H, es una matriz definida simétrica positiva, c es un vector constante y b es una constante. La solución óptima para este problema se da cuando las derivadas parciales de x llegan a cero, es decir,
| (7) |
El punto de solución óptima, x*, se puede escribir como
| (8) |
Los métodos de tipo Newton (en contraste con los métodos quasi-Newton) calculan H directamente y avanzan en una dirección de descenso para localizar el mínimo después de una serie de iteraciones. Calcular H numéricamente conlleva una gran carga de computación. Los métodos quasi-Newton lo evitan usando el comportamiento observado de f(x) y ∇f(x) para acumular información de la curvatura y hacer una aproximación a H usando una técnica de actualización apropiada.
Se han desarrollado un gran número de métodos de actualización de la matriz hessiana. No obstante, se cree que la fórmula de Broyden [3], Fletcher [12], Goldfarb [20] y Shanno [37] (BFGS) es la más efectiva a la hora de usarse en un método general.
La fórmula dada por BFGS es
| (9) |
donde
Como punto de inicio, H0 se puede establecer en cualquier matriz definida simétrica positiva, por ejemplo, la matriz identidad I. Para evitar la inversión de la matriz hessiana H, puede derivar un método de actualización que prevenga la inversión directa de H usando una fórmula que haga una aproximación de la matriz hessiana inversa H–1 en cada actualización. Un procedimiento bien conocido es la fórmula DFP de Davidon [7], Fletcher y Powell [14]. Utiliza la misma fórmula que el método BFGS (Ecuación 9), salvo que qk se sustituye por sk.
La información del gradiente se puede obtener a través de gradientes calculados analíticamente o derivados de derivadas parciales con un método de diferenciación numérica por diferencias finitas. Esto implica perturbar cada una de las variables de diseño, x sucesivamente y calcular la tasa de cambios en la función objetivo.
Por cada iteración mayor, k, se ejecuta una búsqueda de recta en la dirección.
| (10) |
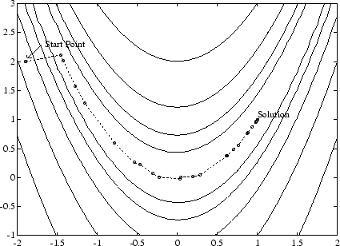
El método quasi-Newton está ilustrado por la ruta de solución en la función de Rosenbrock en Figura 5-2, Método BFGS en la función de Rosenbrock. El método puede seguir la forma del valle y converge en el mínimo después de 140 evaluaciones de función usando únicamente gradientes de diferencia finita.
Figura 5-2, Método BFGS en la función de Rosenbrock
Para una descripción completa de esta figura, incluidos los scripts que generan los puntos iterativos, consulte Minimización de la función banana.
Búsqueda de recta
La búsqueda de recta es un método de búsqueda que se usa como parte de un algoritmo de optimización más grande. En cada paso del algoritmo principal, el método de búsqueda de recta busca a lo largo de la recta que contiene el punto actual, xk, paralelo a la dirección de búsqueda, que es un vector determinado por el algoritmo principal. Es decir, el método encuentra la iteración siguiente xk+1 de la forma
| (11) |
donde xk denota la iteración actual, dk es la dirección de búsqueda y α* es un parámetro escalar de la longitud del paso.
El método de búsqueda de recta pretende disminuir la función objetivo a lo largo de la recta xk + α*dk minimizando de forma repetida los modelos de interpolación polinómica de la función objetivo. El procedimiento de búsqueda de recta tiene dos pasos principales:
La fase de agrupación determina el rango de puntos en la recta que se desea buscar. El paréntesis corresponde a un intervalo que especifica el rango de valores de α.
El paso de seccionamiento divide el paréntesis en subintervalos, en los que el mínimo de la función objetivo se aproxima por interpolación polinómica.
La longitud de paso α resultante satisface las condiciones de Wolfe:
| (12) |
| (13) |
donde c1 y c2 son constantes con 0 < c1 < c2 < 1.
La primera condición (Ecuación 12) requiere que αk disminuya la función objetivo lo suficiente. La segunda condición (Ecuación 13) asegura que la longitud de paso no es demasiado pequeña. Los puntos que satisfacen ambas condiciones (Ecuación 12 y Ecuación 13) se llaman puntos aceptables.
El método de búsqueda de recta es una implementación del algoritmo descrito en la sección 2-6 de [13]. Consulte también [31] para obtener más información sobre la búsqueda de recta.
Actualización de la matriz hessiana
Muchas de las funciones de optimización determinan la dirección de búsqueda actualizando la matriz hessiana en cada iteración con el método BFGS (Ecuación 9). La función fminunc también proporciona una opción para usar el método DFP mencionado en Métodos quasi-Newton (establezca HessUpdate en 'dfp' en options para seleccionar el método DFP). La matriz hessiana, H, siempre se mantiene como definida positiva para que la dirección de la búsqueda, d, esté siempre en una dirección descendente. Esto quiere decir que por algún paso arbitrariamente pequeño α en la dirección d, la función objetivo disminuye en magnitud. Se alcanza la definición positiva de H cuando se asegura que H se ha inicializado para ser definida positiva y, a partir de entonces, (de Ecuación 14) siempre es positiva. El término es un producto del parámetro de longitud de paso de la búsqueda de recta αk y una combinación de la dirección de búsqueda d con evaluaciones de gradiente pasadas y presentes,
| (14) |
Siempre alcanza la condición de que sea positiva llevando a cabo una búsqueda de recta lo suficientemente precisa. Esto se debe a que la dirección de búsqueda, d, es una dirección descendente, de manera que αk y el gradiente negativo –∇f(xk)Td siempre son positivos. Así, el término negativo posible –∇f(xk+1)Td se puede hacer tan pequeño en magnitud como se requiera aumentando la precisión de la búsqueda de recta.
Aproximación de la matriz hessiana LBFGS
Para problemas grandes, el método de aproximación de la matriz hessiana BFGS puede ser relativamente lento y requerir una gran cantidad de memoria. Para sortear estos problemas, utilice el método de aproximación de la matriz hessiana LBFGS estableciendo la opción HessianApproximation en 'lbfgs'. Esto provoca que fminunc utilice la aproximación de la matriz hessiana BFGS de memoria baja, que se describe a continuación. Para conocer las ventajas del uso de la LBFGS en un problema grande, consulte Resolver problemas no lineales con muchas variables.
Tal y como describen Nocedal y Wright [31], la aproximación de la matriz hessiana BFGS de memoria baja es similar a la aproximación de BFGS descrita en Métodos quasi-Newton, pero usa una cantidad limitada de memoria para iteraciones previas. La fórmula de actualización de la matriz hessiana proporcionada en Ecuación 9 es
donde
Otra descripción del procedimiento BFGS es
| (15) |
donde ɑk es la longitud de paso elegida por la búsqueda de recta y Hk es una aproximación de la matriz hessiana inversa. La fórmula para Hk:
donde sk y qk se definen como anteriormente y
Para LBFGS, el algoritmo mantiene un número fijo y finito m de los parámetros sk y qk de las iteraciones inmediatamente precedentes. Empezando por un H0 inicial, el algoritmo calcula una Hk aproximada para obtener el paso de Ecuación 15. La computación de avanza como una recursión de las ecuaciones precedentes usando los valores m más recientes de ρj, qj y sj. Para más información, consulte Algoritmo 7.4 de Nocedal y Wright [31].