rotpat
Rotate radiation pattern
Description
rpat = rotpat(pat,az,el,rotax,expval)az and
el do not cover the entire 3-D space.
Tip
You can use this function to rotate real and complex scalar radiation patterns as well as the orthogonal components of polarized fields. To rotate polarized fields, rotate the horizontal and vertical polarization components separately.
Examples
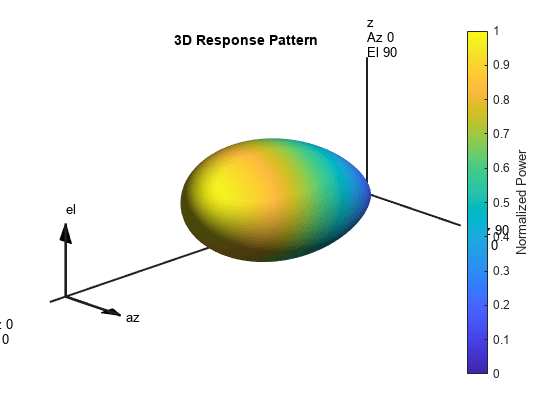
Use a short-dipole antenna to create a polarized radiation pattern. Rotate the pattern and use the rotated pattern as the radiation pattern of a custom antenna.
Create a phased.ShortDipoleAntennaElement antenna object with default properties. The short-dipole antenna radiates polarized radiation. Obtain and display the radiation for all directions.
antenna1 = phased.ShortDipoleAntennaElement; el = -90:90; az = -180:180; pat_h = zeros(numel(el),numel(az),'like',1+1i); pat_v = pat_h; fc = 3e8; for m = 1:numel(el) temp = antenna1(fc,[az;el(m)*ones(1,numel(az))]); pat_h(m,:) = temp.H; pat_v(m,:) = temp.V; end pattern(antenna1,fc,'Type','Power')

Rotate the antenna pattern around the y-axis by 135 degrees followed by a rotation around the x-axis by 65 degrees.
newax = rotx(65)*roty(135); pat2_h = rotpat(pat_h,az,el,newax); pat2_v = rotpat(pat_v,az,el,newax);
Insert the rotated pattern into a phased.CustomAntennaElement object. Set the antenna polarization properties so that the element radiates horizontal and vertical polarized fields. Then display the rotated pattern in three dimensions.
antenna2 = phased.CustomAntennaElement( ... 'SpecifyPolarizationPattern',true, ... 'HorizontalMagnitudePattern',mag2db(abs(pat2_h)), ... 'HorizontalPhasePattern',rad2deg(angle(pat2_h)), ... 'VerticalMagnitudePattern',mag2db(abs(pat2_v)), ... 'VerticalPhasePattern',rad2deg(angle(pat2_v))); pattern(antenna2,fc,'Type','Power')
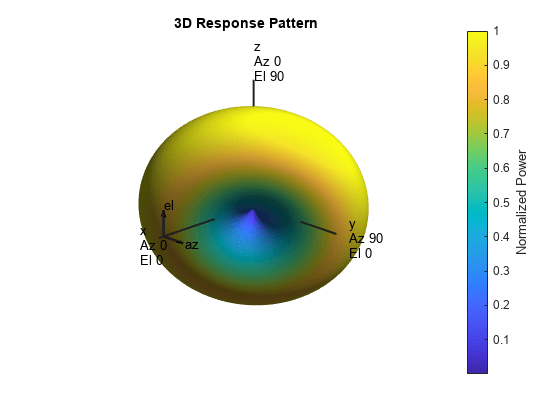
Create a radiation pattern for a cosine antenna using a phased.CosineAntennaElement object. Rotate the pattern to use in a phased.CustomAntennaElement antenna object.
First obtain the radiation pattern for a phased.CosineAntennaElement object over a limited range of directions. The field is not polarized.
antenna1 = phased.CosineAntennaElement('CosinePower',[5,5]); az = -60:65; el = -60:60; pat = zeros(numel(el),numel(az),'like',1); fc = 300e6; for m = 1:numel(el) temp = antenna1(fc,[az;el(m)*ones(1,numel(az))]); pat(m,:) = temp; end
Display the original pattern.
imagesc(az,el,abs(pat)) axis xy axis equal axis tight xlabel('Azimuth (deg)') ylabel('Elevation (deg)') title('Original Radiation Pattern') colorbar

Rotate the antenna pattern by 20 degrees around the z-axis and 50 degrees around the x-axis. Then display the rotated pattern.
newax = rotx(50)*rotz(20); rpat = rotpat(pat,az,el,newax); imagesc(az,el,abs(rpat)) axis xy axis equal axis tight xlabel('Azimuth (deg)') ylabel('Elevation (deg)') title('Rotated Radiation Pattern') colorbar

Use the rotated pattern in a custom antenna element and display the pattern in 3-D.
antenna2 = phased.CustomAntennaElement( ... 'AzimuthAngles',az,'ElevationAngles',el,'SpecifyPolarizationPattern',false, ... 'MagnitudePattern',mag2db(abs(rpat)), ... 'PhasePattern',zeros(size(rpat))); pattern(antenna2,fc,'Type','Power')
Input Arguments
Radiation pattern, specified as a complex-valued
N-by-M matrix or complex-valued
N-by-M-by-L array.
N is the length of the el vector and
M is the length of the az vector. Each column
corresponds to one of the azimuth angles specified in the az
argument. Each row corresponds to one of the elevation angles specified in the
el argument. You can specify multiple radiation patterns using
L pages. For example, you can use pages to specify radiation
patterns at different frequencies. The main lobe of each pattern is assumed to point
along the x-axis. Units are in meters-squared.
Data Types: double
Complex Number Support: Yes
Azimuth angles for computing 3-D radiation pattern, specified as a
1-by-M real-valued row vector where M is the
number of azimuth angles. Each entry corresponds to one of the columns of the matrix
specified in the pat argument. Angle units are in degrees. Azimuth
angles must lie between –180° and 180°, inclusive.
The azimuth angle is the angle between the x-axis and the projection of the direction vector onto the xy-plane. The azimuth angle is positive when measured from the x-axis toward the y-axis.
Example: -45:2:45
Data Types: double
Elevation angles for computing directivity and pattern, specified as a
1-by-N real-valued row vector where N is the
number of elevation angles. Each entry corresponds to one of the rows of the matrix
specified in the pat argument. Angle units are in degrees.
Elevation angles must lie between –90° and 90°, inclusive.
The elevation angle is the angle between the direction vector and xy-plane. The elevation angle is positive when measured toward the z-axis.
Example: -75:1:70
Data Types: double
Rotation matrix, specified as a real-valued orthonormal 3-by-3 matrix or a real-valued 3-by-3-by-P array. The columns represent the x, y, and z directions of the rotated coordinate system with respect to the original coordinate system. The P pages specify different rotation matrices.
This table describes how dimensions of the output pattern rpat
depend on the dimensions of the pat and rotax
arguments.
Dimensions of rpat
Dimensions of pat | Dimensions of
rotax | |
|---|---|---|
| 3-by-3 | 3-by-3-by-P | |
| M-by-N | Rotate a single pattern by a single rotation matrix. Output dimensions of
rpat are
M-by-N. | Rotate a single pattern by P different rotation
matrices. Output dimensions of rpat are
M-by-N-by-P. |
| M-by-N-by-L | Rotate L patterns by the same rotation matrix. Output
dimensions of rpat are
M-by-N-by-L. | In this case, P must equal L and
the function rotates each pattern by the corresponding rotation matrix. Output
dimensions of rpat are
M-by-N-by-L. |
Example: rotx(45)*roty(30)
Data Types: double
Extrapolation value, specified as a scalar. This scalar is the extrapolated value
when the rotated patterns do not fill the entire 3-D space specified by
az and el. In general, consider setting
expval to 0 if the pattern is specified in a linear scale or
-inf if the pattern is specified in a dB scale.
Example: -inf
Data Types: double
Output Arguments
Rotated radiation pattern, returned as a complex-valued
N-by-M matrix or complex-valued
N-by-M-by-P array.
N is the length of the el vector.
M is the length of the az vector. The
dimensionality of pat and rotax determine the
value of P as discussed in the rotax input
argument. Units are in meters-squared.
Data Types: double
Complex Number Support: Yes
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Version History
Introduced in R2019a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)