Generating Guitar Chords Using the Karplus-Strong Algorithm
This example shows how to generate realistic guitar chords using the Karplus-Strong Algorithm and discrete-time filters.
Setup
Begin by defining variables that we will be using later, e.g. the sampling frequency, the first harmonic frequency of the A string, the offset of each string relative to the A string.
Fs = 44100;
A = 110; % The A string of a guitar is normally tuned to 110 Hz
Eoffset = -5;
Doffset = 5;
Goffset = 10;
Boffset = 14;
E2offset = 19;Generate the frequency vector that we will use for analysis.
F = linspace(1/Fs, 1000, 2^12);
Generate 4 seconds of zeros to be used to generate the guitar notes.
x = zeros(Fs*4, 1);
Play a Note on an Open String
When a guitar string is plucked or strummed, it produces a sound wave with peaks in the frequency domain that are equally spaced. These are called the harmonics and they give each note a full sound. We can generate sound waves with these harmonics with discrete-time filter objects.
Determine the feedback delay based on the first harmonic frequency.
delay = round(Fs/A);
Generate an IIR filter whose poles approximate the harmonics of the A string. The zeros are added for subtle frequency domain shaping.
b = firls(42, [0 1/delay 2/delay 1], [0 0 1 1]); a = [1 zeros(1, delay) -0.5 -0.5];
Show the magnitude response of the filter.
[H,W] = freqz(b, a, F, Fs); plot(W, 20*log10(abs(H))); title('Harmonics of an open A string'); xlabel('Frequency (Hz)'); ylabel('Magnitude (dB)');
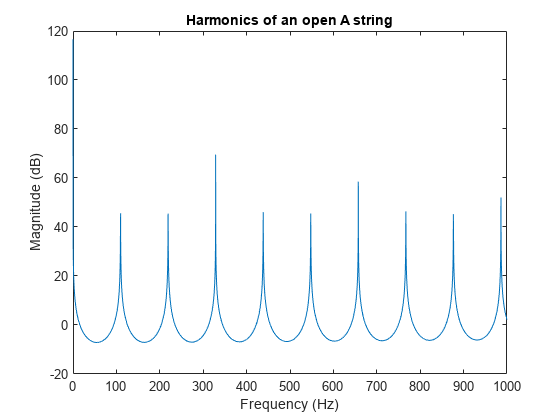
To generate a 4 second synthetic note first we create a vector of states with random numbers. Then we filter zeros using these initial states. This forces the random states to exit the filter shaped into the harmonics.
zi = rand(max(length(b),length(a))-1,1); note = filter(b, a, x, zi);
Normalize the sound for the audioplayer.
note = note-mean(note);
note = note/max(abs(note));
% To hear, type: hplayer = audioplayer(note, Fs); play(hplayer)Play a Note on a Fretted String
Each fret along a guitar's neck allows the player to play a half tone higher, or a note whose first harmonic is higher.
fret = 4; delay = round(Fs/(A*2^(fret/12))); b = firls(42, [0 1/delay 2/delay 1], [0 0 1 1]); a = [1 zeros(1, delay) -0.5 -0.5]; [H,W] = freqz(b, a, F, Fs); hold on plot(W, 20*log10(abs(H))); title('Harmonics of the A string'); legend('Open A string', 'A string on the 4th fret');
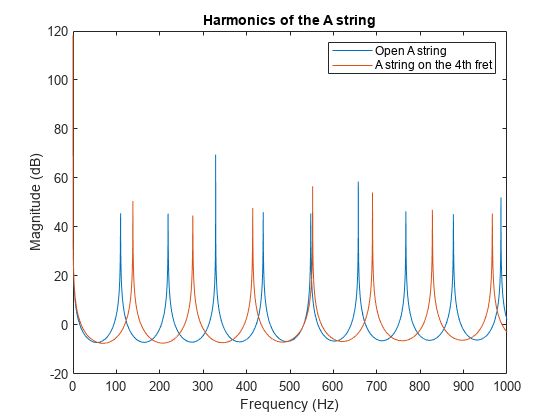
Populate the states with random numbers.
zi = rand(max(length(b),length(a))-1,1);
Create a 4 second note.
note = filter(b, a, x, zi);
Normalize the sound for the audioplayer.
note = note-mean(note);
note = note/max(note);
% To hear, type: hplayer = audioplayer(note, Fs); play(hplayer)Play a Chord
A chord is a group of notes played together whose harmonics enforce each other. This happens when there is a small integer ratio between the two notes, e.g. a ratio of 2/3 would mean that the first notes third harmonic would align with the second notes second harmonic.
Define the frets for a G major chord.
fret = [3 2 0 0 0 3];
Get the delays for each note based on the frets and the string offsets.
delay = [round(Fs/(A*2^((fret(1)+Eoffset)/12))), ... round(Fs/(A*2^(fret(2)/12))), ... round(Fs/(A*2^((fret(3)+Doffset)/12))), ... round(Fs/(A*2^((fret(4)+Goffset)/12))), ... round(Fs/(A*2^((fret(5)+Boffset)/12))), ... round(Fs/(A*2^((fret(6)+E2offset)/12)))]; b = cell(length(delay),1); a = cell(length(delay),1); H = zeros(length(delay),4096); note = zeros(length(x),length(delay)); for indx = 1:length(delay) % Build a cell array of numerator and denominator coefficients. b{indx} = firls(42, [0 1/delay(indx) 2/delay(indx) 1], [0 0 1 1]).'; a{indx} = [1 zeros(1, delay(indx)) -0.5 -0.5].'; % Populate the states with random numbers and filter the input zeros. zi = rand(max(length(b{indx}),length(a{indx}))-1,1); note(:, indx) = filter(b{indx}, a{indx}, x, zi); % Make sure that each note is centered on zero. note(:, indx) = note(:, indx)-mean(note(:, indx)); [H(indx,:),W] = freqz(b{indx}, a{indx}, F, Fs); end
Display the magnitude for all the notes in the chord.
hline = plot(W,20*log10(abs(H.'))); title('Harmonics of a G major chord'); xlabel('Frequency (Hz)'); ylabel('Magnitude (dB)'); legend(hline,'G','B','D','G','B','G2');
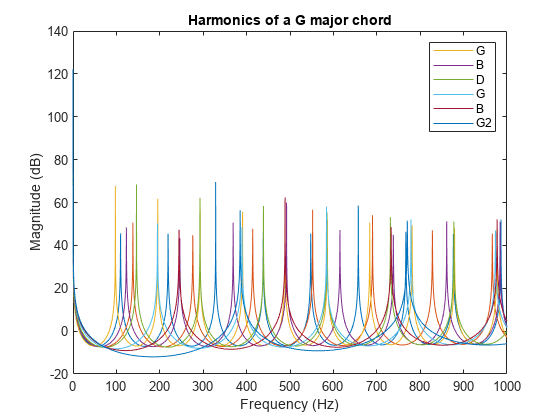
Combine the notes and normalize them.
combinedNote = sum(note,2);
combinedNote = combinedNote/max(abs(combinedNote));
% To hear, type: hplayer = audioplayer(combinedNote, Fs); play(hplayer)Add a Strumming Effect
To add a strumming effect we simply offset each previously created note.
Define the offset between strings as 50 milliseconds.
offset = 50; offset = ceil(offset*Fs/1000);
Add 50 milliseconds between each note by prepending zeros.
for indx = 1:size(note, 2) note(:, indx) = [zeros(offset*(indx-1),1); ... note((1:end-offset*(indx-1)), indx)]; end combinedNote = sum(note,2); combinedNote = combinedNote/max(abs(combinedNote)); % To hear, type: hplayer = audioplayer(combinedNote, Fs); play(hplayer)
