intfilt
Interpolation FIR filter design
Description
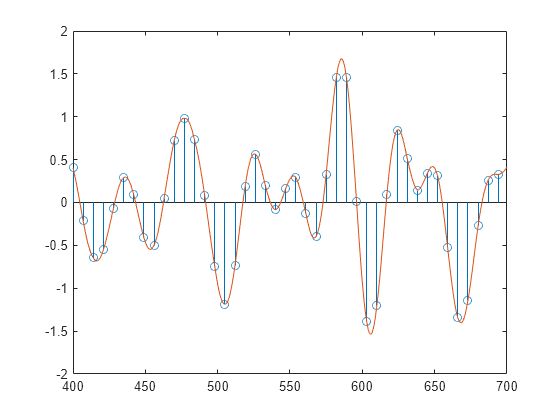
b = intfilt(l,p,alpha)2*p nonzero samples, when used on a sequence
interleaved with l-1 consecutive zeros every l
samples, assuming an original bandlimitedness of alpha times the
Nyquist frequency. The returned filter b is identical to that used by
interp.
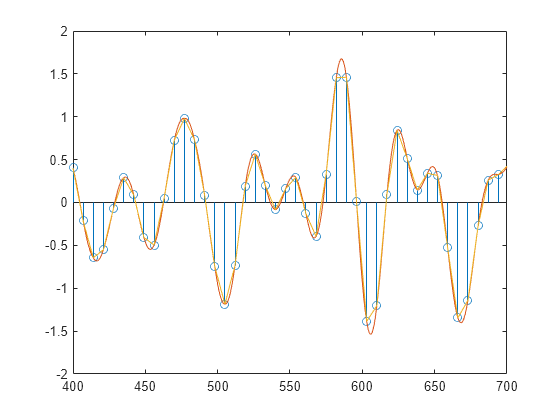
b = intfilt(l,n,'Lagrange')nth-order Lagrange polynomial
interpolation on a sequence interleaved with l-1 consecutive zeros
every l samples.
Examples
Input Arguments
Output Arguments
Algorithms
The bandlimited method uses firls to design an interpolation FIR filter. The
polynomial method uses Lagrange's polynomial interpolation formula on equally spaced samples
to construct the appropriate filter. Both types of filters are basically lowpass and have a
gain of l in the passband.
Extended Capabilities
Version History
Introduced before R2006a
See Also
decimate | downsample | interp | resample | upsample