La función filter

filter se aplica como la estructura de forma directa II traspuesta, donde n–1 es el orden del filtro. Se trata de un formato clásico que presenta el número mínimo de elementos de retardo.

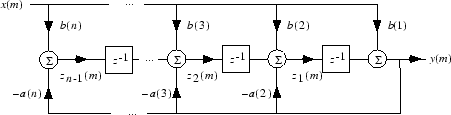
En la muestra m, filter calcula las ecuaciones de diferencias

$$\begin{array}{c}y(m)=b(1)x(m)+z_1(m-1)\\ z_1(m)=b(2)x(m)+z_2(m-1)-a(2)y(m)\\ ⋮=⋮\\ z_{n-2}(m)=b(n-1)x(m)+z_{n-1}(m-1)-a(n-1)y(m)\\ z_{n-1}(m)=b(n)x(m)-a(n)y(m)\end{array}$$

En su formato más básico, filter inicia las salidas de retardo z_i(1), i = 1, ..., n-1 hasta 0. Esto equivale a asumir que las entradas y salidas pasadas son cero. Establezca las salidas de retardo iniciales utilizando un cuarto parámetro de entrada en filter, o bien acceda a las salidas de retardo finales utilizando un segundo parámetro de salida:

[y,zf] = filter(b,a,x,zi)

Acceder a condiciones iniciales y finales resulta útil para filtrar datos en secciones, especialmente si existen limitaciones de memoria. Supongamos que ha recopilado datos en dos segmentos de 5000 puntos cada uno:

x1 = randn(5000,1);  % Generate two random data sequences.
x2 = randn(5000,1); 

Es posible que la primera secuencia, x1, se corresponda con los primeros 10 minutos de datos; y la segunda, x2, con otros 10 minutos. La secuencia completa es x = [x1;x2]. Si no existe memoria suficiente para conservar la secuencia combinada, filtre las subsecuencias x1 y x2 una por una. Para garantizar la continuidad de las secuencias filtradas, utilice las condiciones finales de x1 como condiciones iniciales para filtrar x2:

[y1,zf] = filter(b,a,x1);
y2 = filter(b,a,x2,zf);

La función filtic genera condiciones iniciales para filter. filtic calcula el vector de retardo para que el comportamiento del filtro refleje las entradas y salidas pasadas que especifique. Para obtener los mismos valores de retardo de salida zf de arriba con filtic, utilice

zf = filtic(b,a,flipud(y1),flipud(x1));

Esto puede resultar útil al filtrar secuencias de datos cortas, ya que las condiciones iniciales adecuadas ayudan a reducir los efectos transitorios de inicio.