Local Restriction (2P)

Restriction in flow area in two-phase fluid network

• 

Libraries:
Simscape / Foundation Library / Two-Phase Fluid / Elements

Description

The Local Restriction (2P) block models the pressure drop due to a localized reduction in flow area, such as a valve or an orifice, in a two-phase fluid network.

Ports A and B represent the restriction inlet and outlet. The input physical signal at port AR specifies the restriction area. Alternatively, you can specify a fixed restriction area as a block parameter.

The block icon changes depending on the value of the Restriction type parameter.

Restriction Type	Block Icon
Variable
Fixed

The restriction is adiabatic. It does not exchange heat with the environment.

The restriction consists of a contraction followed by a sudden expansion in flow area.

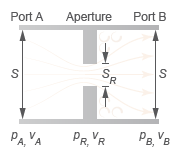
Local Restriction Schematic

The fluid accelerates during the contraction, which causes the pressure to drop. After passing through the restriction with some momentum loss, the fluid expands and decelerates toward the outlet, allowing the pressure to rise slightly after the restriction. This pressure loss model corresponds to the Control volume option of the Pressure loss model parameter. It provides better accuracy but is less robust and efficient than the default Bernoulli option, which assumes uniform fluid density between the restriction inlet and outlet.

Use the Bernoulli option when:

• The local restriction is operating in a fully subcooled liquid regime. The fluid is approximately incompressible and the uniform density assumption is appropriate.

• The local restriction is used as an expansion valve in a refrigeration cycle. The fluid at the inlet is a subcooled liquid coming out of the condenser, therefore the uniform density assumption is appropriate.

• The local restriction is operating in a fully superheated vapor regime, but the flow velocity is low subsonic, which is typically the case in HVAC systems. In this case, the density also does not change much and the uniform density assumption is appropriate.

For all other situations, you can also use the Bernoulli option to trade accuracy for a faster and more robust simulation.

Mass Balance

The mass balance equation is

$${\dot{m}}_A+{\dot{m}}_B=0,$$

where:

• $${\dot{m}}_A$$ and $${\dot{m}}_B$$ are the mass flow rates into the restriction through port A and port B.

Energy Balance

The energy balance equation is

$${\varphi }_A+{\varphi }_B=0,$$

where ϕ_A and ϕ_B are the energy flow rates into the restriction through port A and port B.

The local restriction is assumed to be adiabatic, and therefore, the change in specific total enthalpy is zero. At port A,

$$u_A+p_A{\nu }_A+\frac{w_A^2}{2}=u_R+p_R{\nu }_R+\frac{w_R^2}{2},$$

while at port B,

$$u_B+p_B{\nu }_B+\frac{w_B^2}{2}=u_R+p_R{\nu }_R+\frac{w_R^2}{2},$$

where:

• u_A, u_B, and u_R are the specific internal energies at port A, at port B, and the restriction aperture.

• p_A, p_B, and p_R are the pressures at port A, port B, and the restriction aperture.

• ν_A, ν_B, and ν_R are the specific volumes at port A, port B, and the restriction aperture.

• w_A, w_B, and w_R are the ideal flow velocities at port A, port B, and the restriction aperture.

The block computes the ideal flow velocity as

$$w_A=\frac{{\dot{m}}_{ideal}{\nu }_A}{S}$$

at port A, as

$$w_B=\frac{{\dot{m}}_{ideal}{\nu }_B}{S}$$

at port B, and as

$$w_R=\frac{{\dot{m}}_{ideal}{\nu }_R}{S_R},$$

inside the restriction, where:

• $${\dot{m}}_{ideal}$$ is the ideal mass flow rate through the restriction.

• S is the flow area at port A and port B.

• S_R is the flow area of the restriction aperture.

The block computes the ideal mass flow rate through the restriction as:

$${\dot{m}}_{ideal}=\frac{{\dot{m}}_A}{C_D},$$

where C_D is the flow discharge coefficient for the local restriction.

Local Restriction Variables

Momentum Balance if Using Bernoulli Equation

The mass flow from port A to port B is:

$$\begin{array}{l}{\dot{m}}_A=C_d{S}_{\text{R}}\frac{\Delta p}{{\left(\Delta p+\Delta p_{lam}^2\right)}^{1/4}}\sqrt{\frac{2}{{\nu }_{\text{in}}P{R}_{\text{loss}}\left(1-{\left(\frac{S_R}{S}\right)}^2\right)}},\\ \Delta p=p_{\text{A}}-p_{\text{B}},\end{array}$$

where:

• Δp_lam is the threshold pressure drop at which the flow begins to smoothly transition between laminar and turbulent.

• v_in is the inlet specific volume. Which port serves as the inlet and which serves as the outlet depends on the pressure differential across the restriction. If pressure is greater at port A than at port B, then port A is the inlet; if pressure is greater at port B, then port B is the inlet.

• PR_loss is the pressure loss ratio.

The pressure loss ratio, PR_loss, is the ratio of the pressure difference between the inlet and the outlet to the pressure difference between the inlet and the restriction. It is a term that accounts for the pressure recovery during the flow expansion after the restriction:

$$P{R}_{loss}=\frac{\sqrt{1-{\left(\frac{S_{\text{R}}}{S}\right)}^2\left(1-C_d^2\right)}-C_d\frac{S_{\text{R}}}{S}}{\sqrt{1-{\left(\frac{S_{\text{R}}}{S}\right)}^2\left(1-C_d^2\right)}+C_d\frac{S_{\text{R}}}{S}}.$$

Momentum Balance if Using Control Volume Analysis

The mass flow from port A to port B for turbulent flow is:

$${\dot{m}}_A=C_d{S}_{\text{R}}\Delta p\sqrt{\frac{2}{\left|\Delta p\right|{\nu }_{\text{R}}{K}_{\text{T}}}}.$$

K_T is defined as:

$$K_{\text{T}}=\left(1+\frac{S_{\text{R}}}{S}\right)\left(1-\frac{{\nu }_{\text{in}}}{{\nu }_{\text{R}}}\frac{S_{\text{R}}}{S}\right)-2\frac{S_{\text{R}}}{S}\left(1-\frac{{\nu }_{\text{out}}}{{\nu }_{\text{R}}}\frac{S_{\text{R}}}{S}\right),$$

where the subscript in denotes the inlet port and the subscript out the outlet port. Which port serves as the inlet and which serves as the outlet depends on the pressure differential across the restriction. If pressure is greater at port A than at port B, then port A is the inlet; if pressure is greater at port B, then port B is the inlet.

The mass flow rate from port A to port B for laminar flow is:

$${\dot{m}}_A=C_d{S}_{\text{R}}\Delta p\sqrt{\frac{2}{\Delta p_{\text{lam}}{\nu }_{\text{R}}{\left(1-\frac{S_{\text{R}}}{S}\right)}^2}}.$$

Δp_lam denotes the threshold pressure drop at which the flow begins to smoothly transition between laminar and turbulent:

$$\Delta p_{\text{lam}}=\left(\frac{p_{\text{A}}+p_{\text{B}}}{2}\right)\left(1-B_{\text{lam}}\right),$$

where B_lam is the Laminar flow pressure ratio parameter. The flow is laminar if the pressure drop from port A to port B is below the threshold value; otherwise, the flow is turbulent.

The pressure at the restriction area, p_R, also depends on the flow regime. When the flow is turbulent:

$$p_{\text{R,T}}=p_{\text{in}}-\frac{{\nu }_{\text{R}}}{2}{\left(\frac{{\dot{m}}_A}{C_d{S}_{\text{R}}}\right)}^2\left(1+\frac{S_{\text{R}}}{S}\right)\left(1-\frac{{\nu }_{\text{in}}}{{\nu }_{\text{R}}}\frac{S_{\text{R}}}{S}\right).$$

When the flow is laminar:

$$p_{\text{R,L}}=\frac{p_{\text{A}}+p_{\text{B}}}{2}.$$

Assumptions and Limitations

• The restriction is adiabatic. It does not exchange heat with its surroundings.

• The Bernoulli pressure loss model assumes uniform fluid density between the inlet and the outlet of the restriction.

Ports

Input

AR — Restriction area control signal, m^2

physical signal

Input physical signal that controls the flow restriction area. The signal saturates when its value is outside the minimum and maximum restriction area limits, specified by the Minimum restriction area and Maximum restriction area parameters.

Dependencies

To enable this port, set the Restriction type parameter to Variable.

Conserving

A — Inlet or outlet

two-phase fluid

Two-phase fluid conserving port associated with the inlet or outlet of the local restriction. The block has no intrinsic directionality.

B — Inlet or outlet

two-phase fluid

Two-phase fluid conserving port associated with the inlet or outlet of the local restriction. The block has no intrinsic directionality.

Parameters

Restriction type — Whether restriction area can change during simulation

Variable (default) | Fixed

Whether the restriction area can change during simulation:

• Variable — The input physical signal at port AR specifies the restriction area, which can vary during simulation. The Minimum restriction area and Maximum restriction area parameters specify the lower and upper bounds for the restriction area.

• Fixed — The restriction area, specified by the Restriction area block parameter value, remains constant during simulation.

Minimum restriction area — Lower bound for restriction cross-sectional area

1e-10 m^2 (default) | positive scalar

Lower bound for the restriction cross-sectional area. You can use this parameter to represent the leakage area. The input signal at port AR saturates at this value to prevent the restriction area from further decreasing.

Dependencies

To enable this parameter, set Restriction type to Variable.

Maximum restriction area — Upper bound for restriction cross-sectional area

0.005 m^2 (default) | positive scalar

Upper bound for the restriction cross-sectional area. The input signal at port AR saturates at this value to prevent the restriction area from further increasing.

Dependencies

To enable this parameter, set Restriction type to Variable.

Restriction area — Area normal to flow path at restriction

1e-3 m^2 (default) | positive scalar

Area normal to the flow path at the restriction.

Dependencies

To enable this parameter, set Restriction type to Fixed.

Pressure loss model — Whether to assume uniform fluid density for momentum balance calculation

Bernoulli (default) | Control volume

Equations to use for momentum balance calculation:

• Bernoulli — The block uses the Bernoulli equation, which assumes uniform density from inlet to outlet. This option is sometimes less accurate than the Control volume method, but it is more robust and provides faster simulation.

• Control volume — The block uses the control volume analysis without assuming uniform density. It models the flow from the inlet to the restriction as a flow contraction and the flow from the restriction to the outlet as a flow expansion.

Cross-sectional area at ports A and B — Area normal to flow path at ports

0.01 m^2 (default) | positive scalar

Area normal to the flow path at ports A and B. This area is assumed to be the same for both ports.

Discharge coefficient — Ratio of actual mass flow rate to theoretical mass flow rate through restriction

0.64 (default) | unitless scalar between 0 and 1

The discharge coefficient is a semi-empirical parameter commonly used to characterize the flow capacity of an orifice. This parameter represents the ratio of the actual mass flow rate through the orifice to the ideal mass flow rate.

Laminar flow pressure ratio — Pressure ratio for switching between laminar and turbulent regimes

0.999 (default) | unitless scalar between 0 and 1

Ratio of the outlet to the inlet port pressure at which the flow regime is assumed to switch from laminar to turbulent. The prevailing flow regime determines the equations used in simulation. If the flow is laminar, the pressure drop across the restriction is linear with respect to the mass flow rate. If the flow is turbulent, the pressure drop across the restriction is quadratic with respect to the mass flow rate.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2015b

R2024a: Use Bernoulli equation to compute pressure losses

The Local Restriction (2P) block now has the Pressure loss model parameter, which lets you choose between two pressure loss models. The Control volume option, which is the functionality available in previous releases, is more accurate in certain scenarios. The new Bernoulli option, which assumes uniform fluid density from inlet to outlet, is more robust and provides faster simulation.

This change has no compatibility impact. The Bernoulli option is the default setting for new blocks, but when you open an existing model, the Local Restriction (2P) blocks in it automatically have the Pressure loss model parameter set to Control volume.

R2022b: Model both fixed and variable area restrictions

The Local Restriction (2P) block now has the Restriction type parameter, which lets you switch between modeling fixed and variable area restrictions. The block uses either the Restriction area parameter or the input physical signal port AR to specify the area of the local restriction.

In previous releases, the block modeled only fixed restrictions. The Two-Phase Fluid library also contained a separate Variable Local Restriction (2P) block, which is no longer available. This change has no compatibility impact. When you open an existing model, all Variable Local Restriction (2P) blocks in it are automatically replaced by Local Restriction (2P) blocks with an exposed control port AR.