Enforce Barrier Certificate Constraints for Collision-Free Robots
This example shows how to enforce barrier certificate constraints for collision-free robots using the Barrier Certificate Enforcement block.
Overview
In this example, the goal for the robots is to reach a target position without colliding with each other [1]. The robot dynamics are modeled by double integrators in the x-y plane. Each robot has four states (x-position, y-position, x-velocity, and y-velocity) and two control variables (x-acceleration and y-acceleration). The velocities are constrained to [-2, 2] m/s and the accelerations are constrained to [-10, 10] m/s^2. The PID controllers are designed for the robots to reach the target position. Collision avoidance is achieved by enforcing barrier certificate constraints.
Open the Simulink® model.
mdl = 'twoRobotsCBF';
open_system(mdl);
Controller Design
Each robot has its own controller that brings it to the target position. In this example, the controller is implemented as a PID-type controller.
Run the simulation and view the results.
constrained = 0; sim(mdl);


In the figure, robot 1 (green) reaches the target position [4.9, 4.8] m and robot 2 reaches the target position [0, 0] m. The controllers successfully bring the controlled robots to their target positions.
Open the distance scope in the Two robots > visualization subsystem. The two robots collide with each other at around 1.3 seconds.

Barrier Certificate Constraints
For collision avoidance, the constraint is that the distance between two robots and stay greater than a given threshold if the two robots are moving closer to each other [1]. The barrier certificate is given by
.
Here, the variables are:
The maximum braking power from both robots —
The minimum distance between the robots —
The position error vector —
The velocity error vector —
The partial derivative of over states is denoted by , and the analytical results are given in the barrierGradFcn2Robots script.
The Barrier Certificate Enforcement block accepts the dynamics in the form . For this example,
and ,
and each element is a 2-by-2 matrix.
Simulate Collision-Free Controller with Barrier Certificate Constraint
To view the constraint implementation, open the Constraint > Constrained subsystem.
constrained = 1;

Close the figure before running the model.
f = findobj('Name','Two robots'); close(f)
Run the model and view the simulation results. The two robots avoid each other when they are too close.
sim(mdl);

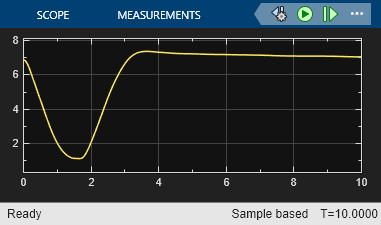
The distance between the two robots stays above the threshold .
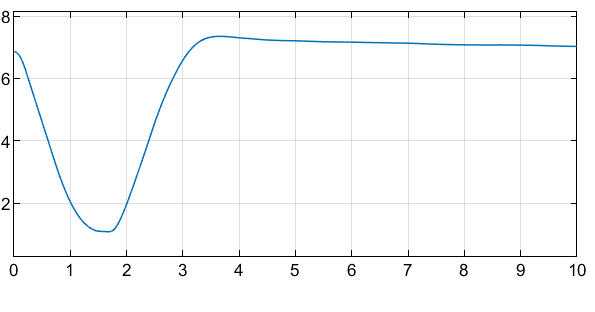
The Barrier Certificate Enforcement block successfully constrains the control actions such that the two robots reach their target positions in a collision-free manner.
bdclose(mdl) f = findobj('Name','Two robots'); close(f)
References
[1] Wang, Li, Aaron D. Ames, and Magnus Egerstedt. “Safety Barrier Certificates for Collisions-Free Multirobot Systems.” IEEE Transactions on Robotics 33, no. 3 (June 2017): 661–74. https://doi.org/10.1109/TRO.2017.2659727.
See Also
Barrier Certificate Enforcement