Distributed Parameters Line
(To be removed) Implement N-phase distributed parameter transmission line model with lumped losses
The Specialized Power Systems library will be removed in R2026a. Use the Simscape™ Electrical™ blocks and functions instead. For more information on updating your models, see Upgrade Specialized Power System Models to use Simscape Electrical Blocks.
Libraries:
Simscape /
Electrical /
Specialized Power Systems /
Power Grid Elements
Description
The Distributed Parameters Line block implements an N-phase distributed parameter line model with lumped losses. The model is based on the Bergeron's traveling wave method used by the Electromagnetic Transient Program (EMTP) [1]. In this model, the lossless distributed LC line is characterized by two values (for a single-phase line): the surge impedance and the wave propagation speed . l and c are the per-unit length inductance and capacitance.
The figure shows the two-port model of a single-phase line.
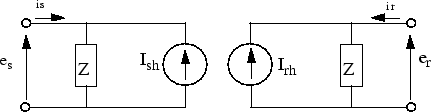
For a lossless line (r = 0), the quantity e + Zci, where e is the line voltage at one end and i is the line current entering the same end, must arrive unchanged at the other end after a transport delay τ.
where d is the line length and v is the propagation speed.
The model equations for a lossless line are:
knowing that
In a lossless line, the two current sources Ish and Irh are computed as:
When losses are taken into account, new equations for Ish and Irh are obtained by lumping R/4 at both ends of the line and R/2 in the middle of the line:
R = total resistance = r × d
The current sources Ish and Irh are then computed as follows:
where
r, l, c are the per unit length parameters, and d is the line length. For a lossless line, r = 0, h = 1, and Z = Zc.
For multiphase line models, modal transformation is used to convert line quantities from phase values (line currents and voltages) into modal values independent of each other. The previous calculations are made in the modal domain before being converted back to phase values.
In comparison to the PI section line model, the distributed line represents wave propagation phenomena and line end reflections with much better accuracy.
Assumptions and Limitations
This model does not represent accurately the frequency dependence of RLC parameters of real power lines. Indeed, because of the skin effects in the conductors and ground, the R and L matrices exhibit strong frequency dependence, causing an attenuation of the high frequencies.
Ports
Conserving
Parameters
References
[1] Dommel, H., “Digital Computer Solution of Electromagnetic Transients in Single and Multiple Networks,” IEEE® Transactions on Power Apparatus and Systems, Vol. PAS-88, No. 4, April, 1969.
Extended Capabilities
Version History
Introduced before R2006a