Three-Phase PI Section Line

Implement three-phase transmission line section with lumped parameters

• 

Libraries:
Simscape / Electrical / Specialized Power Systems / Power Grid Elements

Description

The Three-Phase PI Section Line block implements a balanced three-phase transmission line model with parameters lumped in a PI section.

Contrary to the Distributed Parameters Line model where the resistance, inductance, and capacitance are uniformly distributed along the line, the Three-Phase PI Section Line block lumps the line parameters in a single PI section as shown in the figure below.

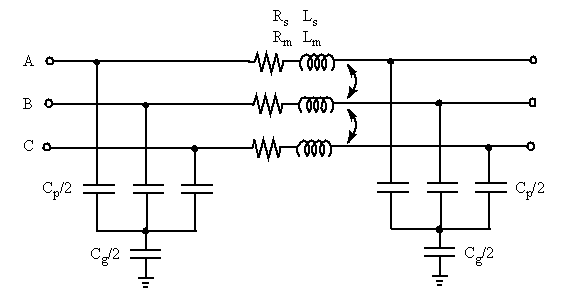
The line parameters R, L, and C are specified as positive- and zero-sequence parameters that take into account the inductive and capacitive couplings between the three phase conductors, as well as the ground parameters. This method of specifying line parameters assumes that the three phases are balanced.

The self and mutual resistances (Rs, Rm), self and mutual inductances (Ls, Lm) of the three coupled inductors, as well as phase capacitances Cp and ground capacitances Cg, are deduced from the positive- and zero-sequence RLC parameters as follows.

Let us assume the following line parameters:

r1, r0	Positive- and zero-sequence resistances per unit length (Ω/km)
l1, l0	Positive- and zero-sequence inductances per unit length (H/km)
c1, c0	Positive- and zero-sequence capacitances per unit length (F/km)
f	Frequency (Hz)
lsec	Line section length (km)

The total positive- and zero-sequence RLC parameters including hyperbolic corrections are first evaluated:

$$\begin{array}{l}{R}_1=r_1\cdot l\sec \cdot k_{r1}\\ L_1=l_1\cdot l\sec \cdot k_{l1}\\ C_1=c_1\cdot l\sec \cdot k_{c1}\\ R_0=r_0\cdot l\sec \cdot k_{r0}\\ L_0=l_0\cdot l\sec \cdot k_{l0}\\ C_0=c_0\cdot l\sec \cdot k_{c0}\end{array}$$

where

k_r1, k_l1, k_c1, k_r0, k_l0, k_c0 — positive-sequence and zero-sequence hyperbolic correction factors

Note

See the PI Section Line block reference page for an explanation on how to compute RLC parameters taking into account hyperbolic corrections.

The Powergui block provides a graphical tool for the calculation of resistance, inductance, and capacitance per unit length based on the line geometry and the conductor characteristics. See the power_lineparam reference page to learn how to use this tool.

For a short line section (approximately lsec < 50 km), these correction factors are negligible (close to unity). However, for long lines, these hyperbolic corrections must be taken into account in order to get an exact line model at the specified frequency.

The RLC line section parameters are then computed as follows:

$$\begin{array}{l}Rs=\left(2R_1+R_0\right)/3\\ Ls=\left(2L_1+L_0\right)/3\\ R_m=\left(R_0-R_1\right)/3\\ L_m=\left(L_0-L_1\right)/3\\ C_p=C_1\\ C_g=3C_1{C}_0/\left(C_1-C_0\right)\end{array}$$

Examples

Single-Phase Energization of a Three-Phase Line

Transients obtained with a distributed parameter line model and a PI section line model.

• Open Model

Ports

Conserving

A — Phase A terminal

specialized electrical

Specialized electrical conserving port associated with the terminal of phase A.

B — Phase B terminal

specialized electrical

Specialized electrical conserving port associated with the terminal of phase B.

C — Phase C terminal

specialized electrical

Specialized electrical conserving port associated with the terminal of phase C.

Parameters

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Line length (km) — Line section length

100 (default) | positive scalar

Line section length in kilometers (km).

Frequency used for rlc specification (Hz) — Frequency used for specification of per unit length rlc line parameters

60 (default) | positive scalar

Frequency used for specification of per unit length rlc line parameters, in hertz (Hz). This is usually the nominal system frequency (50 Hz or 60 Hz).

Positive- and zero-sequence resistances (Ohms/km) [r1 r0] — Positive- and zero-sequence resistances

[ 0.01273 0.3864] (default) | vector of two positive elements

Positive- and zero-sequence resistances in ohms/kilometer (Ω/km).

Positive- and zero-sequence inductances (H/km) [l1 l0] — Positive- and zero-sequence inductances

[ 0.9337e-3 4.1264e-3] (default) | vector of two positive elements

Positive- and zero-sequence inductances in henries/kilometer (H/km). The zero-sequence inductance cannot be zero, because it would result in an invalid propagation speed computation.

Positive- and zero-sequence capacitances (F/km) [c1 c0] — Positive- and zero-sequence capacitances

[12.74e-9 7.751e-9] (default) | vector of two positive elements

Positive- and zero-sequence capacitances in farads/kilometer (F/km). The zero-sequence capacitance cannot be zero, because it would result in an invalid propagation speed computation.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced before R2006a