Integrar funciones de MATLAB en gráficos de Stateflow

Para implementar algoritmos complejos en el gráfico de Stateflow®, utilice las funciones de MATLAB®. Las funciones de MATLAB permiten combinar prestaciones matemáticas de MATLAB en el gráfico de Stateflow. Para obtener más información sobre cómo crear funciones de MATLAB, consulte Reuse MATLAB Code by Defining MATLAB Functions.

Tipos de funciones compatibles

Los gráficos de Stateflow pueden llamar a estos tipos de funciones de MATLAB:

  • Funciones locales que se definen en el cuerpo de la función.

  • Funciones gráficas, de Simulink® y de tabla de verdad.

  • Funciones de MATLAB integradas que admiten la generación de código.

  • Funciones extrínsecas para ejecución solo en simulación. Para obtener más información, consulte Llamar a funciones de MATLAB extrínsecas en gráficos de Stateflow.

Añadir funciones de MATLAB a un gráfico de Stateflow

En este ejemplo, se construye un modelo que contiene dos funciones de MATLAB y se utilizan para calcular la media y la desviación estándar de los datos que se introducen en el gráfico.

Configurar el modelo

  1. Cree un nuevo modelo de Simulink.

  2. Añada estos bloques al modelo:

    • Bloque Chart

    • Bloque Constant

    • Dos bloques Display

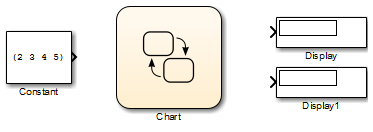
  3. Simulink model that contains a Stateflow chart, a constant block, and two display blocks.

  4. Guarde el modelo como call_stats_function_stateflow.

Configurar el gráfico de Stateflow

  1. Abra el bloque Chart.

  2. Añada dos funciones de MATLAB utilizando el icono de función de MATLAB .

  3. Etiquete las funciones con estas firmas:

    • meanout = meanstats(vals)

    • stdevout = stdevstats(vals)

      Stateflow chart with two MATLAB functions called meanstats and stdevstats.

  4. Añada una transición predeterminada a una intersección final con esta acción de condición: 

    {
mean = meanstats(invals);
stdev = stdevstats(invals);
}

    Stateflow chart with a transition that calls the two MATLAB functions.

    Si los argumentos de una firma de función son escalares, compruebe que las entradas y salidas de las llamadas a función sigan las reglas de la expansión escalar. Para obtener más información, consulte Asignar valores a todos los elementos de una matriz.

Definir elementos de datos

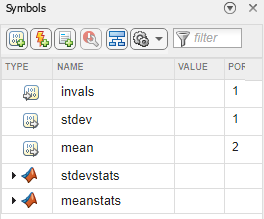
  1. Abra el panel Symbols.

  2. Establezca los tipos de datos para estos datos utilizando la columna Type:

    • invals: Input Data

    • stdev: Output Data

    • mean: Output Data

    The data in the symbols pane.

Programar la función de desviación estándar

Abra la función stdevstats y añada este código:

function stdevout = stdevstats(vals)
%#codegen

% Calculate standard deviation
len = length(vals);
stdevout = sqrt(sum(((vals-avg(vals,len)).^2))/len);

function meanfcn = avg(inputArray,inputSize)
    meanfcn = sum(inputArray)/inputSize;

La función sum calcula el valor de stdevout. La directiva de compilación %#codegen ayuda a detectar infracciones en tiempo de compilación de sintaxis y semántica en funciones de MATLAB que admiten la generación de código.

Programar la función de media

Abra la función meanstats y añada este código:

function meanout = meanstats(vals)
%#codegen

% Calculate statistical mean
len = length(vals);
meanout = avg(vals,len);

% Plot results (simulation only)
coder.extrinsic("plot");
plot(vals,"-+");

function meanfcn = avg(inputArray,inputSize)
    meanfcn = sum(inputArray)/inputSize;

La función length admite la generación de código y devuelve la longitud de un vector. La función avg calcula el valor de meanout. Se define plot como extrínseca, ya que no se admite para la generación de código.

Simular el modelo

Para simular el modelo, conecte primero los bloques de Simulink a los puertos de entrada y de salida del gráfico.

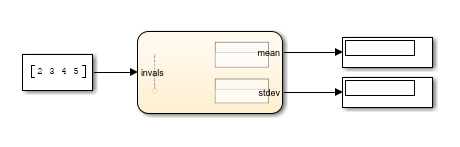
The Simulink model is connected to Stateflow.

Haga clic en Run. Los números de la media y la desviación estándar aparecen en la ventana del bloque Display.

The Display blocks show the results of simulation.

Requisitos para la generación de código

Para generar código, todas las funciones deben admitir la generación de código. Si una función no admite la generación de código, puede utilizar coder.extrinsic (Simulink) para marcarla como una excepción. Para ver una lista de funciones que MATLAB admite para la generación de código, consulte Funciones y objetos admitidos con la generación de código C/C++ (MATLAB Coder).

Consulte también

(Simulink)

Temas