loss
Loss of naive Bayes incremental learning classification model on batch of data
Since R2021a
Description
loss returns the classification loss of a configured
naive Bayes classification model for incremental learning (incrementalClassificationNaiveBayes object).
To measure model performance on a data stream and store the results in the output model,
call updateMetrics or updateMetricsAndFit.
Examples
Three different ways to measure performance of an incremental model on streaming data exist:
Cumulative metrics measure the performance since the start of incremental learning.
Window metrics measure the performance on a specified window of observations. The metrics are updated every time the model processes the specified window.
The
lossfunction measures the performance on a specified batch of data only.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Create a naive Bayes classification model for incremental learning. Specify the class names and a metrics window size of 1000 observations. Configure the model for loss by fitting it to the first 10 observations.
Mdl = incrementalClassificationNaiveBayes('ClassNames',unique(Y),'MetricsWindowSize',1000); initobs = 10; Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs)); canComputeLoss = (size(Mdl.DistributionParameters,2) == Mdl.NumPredictors) + ... (size(Mdl.DistributionParameters,1) > 1) > 1
canComputeLoss = logical
1
Mdl is an incrementalClassificationNaiveBayes model. All its properties are read-only.
Simulate a data stream, and perform the following actions on each incoming chunk of 500 observations:
Call
updateMetricsto measure the cumulative performance and the performance within a window of observations. Overwrite the previous incremental model with a new one to track performance metrics.Call
lossto measure the model performance on the incoming chunk.Call
fitto fit the model to the incoming chunk. Overwrite the previous incremental model with a new one fitted to the incoming observations.Store all performance metrics to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 500; nchunk = floor((n - initobs)/numObsPerChunk); mc = array2table(zeros(nchunk,3),'VariableNames',["Cumulative" "Window" "Chunk"]); % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); mc{j,["Cumulative" "Window"]} = Mdl.Metrics{"MinimalCost",:}; mc{j,"Chunk"} = loss(Mdl,X(idx,:),Y(idx)); Mdl = fit(Mdl,X(idx,:),Y(idx)); end
Now, Mdl is an incrementalClassificationNaiveBayes model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetrics checks the performance of the model on the incoming observations, and then the fit function fits the model to those observations. loss is agnostic of the metrics warm-up period, so it measures the minimal cost for every chunk.
To see how the performance metrics evolve during training, plot them.
figure plot(mc.Variables) xlim([0 nchunk]) ylim([0 0.1]) ylabel('Minimal Cost') xline(Mdl.MetricsWarmupPeriod/numObsPerChunk + 1,'r-.') legend(mc.Properties.VariableNames) xlabel('Iteration')
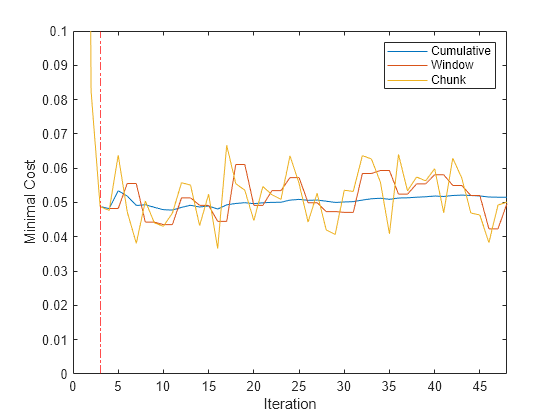
The yellow line represents the minimal cost on each incoming chunk of data. After the metrics warm-up period, Mdl tracks the cumulative and window metrics.
Fit a naive Bayes classification model for incremental learning to streaming data, and compute the multiclass cross entropy loss on the incoming chunks of data.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(1); % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Create a naive Bayes classification model for incremental learning. Configure the model as follows:
Specify the class names.
Specify a metrics warm-up period of 1000 observations.
Specify a metrics window size of 2000 observations.
Track the multiclass cross entropy loss to measure the performance of the model. Create an anonymous function that measures the multiclass cross entropy loss of each new observation, and include a tolerance for numerical stability. Create a structure array containing the name
CrossEntropyand its corresponding function handle.Compute the classification loss by fitting the model to the first 10 observations.
tolerance = 1e-10; crossentropy = @(z,zfit,w,cost)-log(max(zfit(z),tolerance)); ce = struct("CrossEntropy",crossentropy); Mdl = incrementalClassificationNaiveBayes('ClassNames',unique(Y),'MetricsWarmupPeriod',1000, ... 'MetricsWindowSize',2000,'Metrics',ce); initobs = 10; Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));
Mdl is an incrementalClassificationNaiveBayes model object configured for incremental learning.
Perform incremental learning. At each iteration:
Simulate a data stream by processing a chunk of 100 observations.
Call
updateMetricsto compute cumulative and window metrics on the incoming chunk of data. Overwrite the previous incremental model with a new one fitted to overwrite the previous metrics.Call
lossto compute the cross entropy on the incoming chunk of data. Whereas the cumulative and window metrics require that custom losses return the loss for each observation,lossrequires the loss for the entire chunk. Compute the mean of the losses within a chunk.Call
fitto fit the incremental model to the incoming chunk of data.Store the cumulative, window, and chunk metrics to see how they evolve during incremental learning.
% Preallocation numObsPerChunk = 100; nchunk = floor((n - initobs)/numObsPerChunk); tanloss = array2table(zeros(nchunk,3),'VariableNames',["Cumulative" "Window" "Chunk"]); % Incremental fitting for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; Mdl = updateMetrics(Mdl,X(idx,:),Y(idx)); tanloss{j,1:2} = Mdl.Metrics{"CrossEntropy",:}; tanloss{j,3} = loss(Mdl,X(idx,:),Y(idx),'LossFun',@(z,zfit,w,cost)mean(crossentropy(z,zfit,w,cost))); Mdl = fit(Mdl,X(idx,:),Y(idx)); end
Mdl is an incrementalClassificationNaiveBayes model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetrics checks the performance of the model on the incoming observations, and then the fit function fits the model to those observations.
Plot the performance metrics to see how they evolve during incremental learning.
figure h = plot(tanloss.Variables); xlim([0 nchunk]) ylabel('Cross Entropy') xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'r-.') xlabel('Iteration') legend(h,tanloss.Properties.VariableNames)

The plot suggests the following:
updateMetricscomputes the performance metrics after the metrics warm-up period only.updateMetricscomputes the cumulative metrics during each iteration.updateMetricscomputes the window metrics after processing 2000 observations (20 iterations).Because
Mdlis configured to predict observations from the beginning of incremental learning,losscan compute the cross entropy on each incoming chunk of data.
Input Arguments
Naive Bayes classification model for incremental learning, specified as an incrementalClassificationNaiveBayes model object. You can create Mdl directly or by converting a supported, traditionally trained machine learning model using the incrementalLearner function. For more details, see the corresponding reference page.
You must configure Mdl to compute its loss on a batch of observations.
If
Mdlis a converted, traditionally trained model, you can compute its loss without any modifications.Otherwise, you must fit the input model
Mdlto data that contains all expected classes. That is,Mdl.DistributionParametersmust be a cell matrix withMdl.NumPredictorscolumns and at least one row, where each row corresponds to each class name inMdl.ClassNames.
Batch of predictor data with which to compute the loss, specified as an
n-by-Mdl.NumPredictors floating-point
matrix.
The length of the observation labels Y and the number of
observations in X must be equal;
Y( is the label of observation
j (row) in j)X.
Data Types: single | double
Batch of labels with which to compute the loss, specified as a categorical, character, or string array; logical or floating-point vector; or cell array of character vectors.
The length of the observation labels Y and the number of
observations in X must be equal;
Y( is the label of observation
j (row) in j)X.
If Y contains a label that is not a member of
Mdl.ClassNames, loss issues an error.
The data type of Y and Mdl.ClassNames must be the
same.
Data Types: char | string | cell | categorical | logical | single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'LossFun','classiferror','Weights',W specifies returning the misclassification error rate, and the observation weights W.
Cost of misclassifying an observation, specified as a value in the table, where
c is the number of classes in Mdl.ClassNames.
The specified value overrides the value of Mdl.Cost.
| Value | Description |
|---|---|
| c-by-c numeric matrix |
|
| Structure array | A structure array having two fields:
|
Example: Cost=struct('ClassNames',Mdl.ClassNames,'ClassificationCosts',[0 2; 1 0])
Data Types: single | double | struct
Loss function, specified as a built-in loss function name or function handle.
The following table lists the built-in loss function names. You can specify more than one by using a string vector.
| Name | Description |
|---|---|
"binodeviance" | Binomial deviance |
"classiferror" | Misclassification error rate |
"exponential" | Exponential |
"hinge" | Hinge |
"logit" | Logistic |
"mincost" | Minimal expected misclassification cost |
"quadratic" | Quadratic |
For more details, see Classification Loss.
To specify a custom loss function, use function handle notation. The function must have this form:
lossval = lossfcn(C,S,W,Cost)
The output argument
lossvalis an n-by-1 floating-point vector, where n is the number of observations inX. The value inlossval(is the classification loss of observationj)jYou specify the function name (
lossfcnCis an n-by-K logical matrix with rows indicating the class to which the corresponding observation belongs.Kis the number of distinct classes (numel(Mdl.ClassNames), and the column order corresponds to the class order in theClassNamesproperty. CreateCby settingC(=p,q)1, if observationpqp0.Sis an n-by-K numeric matrix of predicted classification scores.Sis similar to thePosterioroutput ofpredict, where rows correspond to observations in the data and the column order corresponds to the class order in theClassNamesproperty.S(is the classification score of observationp,q)pqWis an n-by-1 numeric vector of observation weights.Costis a K-by-K numeric matrix of misclassification costs.
Example: 'LossFun',"classiferror"
Example: 'LossFun',@lossfcn
Data Types: char | string | function_handle
Prior class probabilities, specified as a value in this numeric vector. Prior has the same length as the number of classes in Mdl.ClassNames, and the order of the elements corresponds to the class order in Mdl.ClassNames. loss normalizes the vector so that the sum of the result is 1.
The specified value overrides the value of Mdl.Prior.
Data Types: single | double
Score transformation function describing how incremental learning functions transform raw response values, specified as a character vector, string scalar, or function handle. The specified value overrides the value of Mdl.ScoreTransform.
This table describes the available built-in functions for score transformation.
| Value | Description |
|---|---|
"doublelogit" | 1/(1 + e–2x) |
"invlogit" | log(x / (1 – x)) |
"ismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to 0 |
"logit" | 1/(1 + e–x) |
"none" or "identity" | x (no transformation) |
"sign" | –1 for x < 0 0 for x = 0 1 for x > 0 |
"symmetric" | 2x – 1 |
"symmetricismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to –1 |
"symmetriclogit" | 2/(1 + e–x) – 1 |
Data Types: char | string
Chunk of observation weights, specified as a floating-point vector of positive values.
loss weighs the observations in X
with the corresponding values in Weights. The size of
Weights must equal n, the number of
observations in X.
By default, Weights is ones(.n,1)
For more details, including normalization schemes, see Observation Weights.
Data Types: double | single
Output Arguments
Classification loss, returned as a numeric scalar. L is a measure of model quality. Its interpretation depends on the loss function and weighting scheme.
More About
Classification loss functions measure the predictive inaccuracy of classification models. When you compare the same type of loss among many models, a lower loss indicates a better predictive model.
Consider the following scenario.
L is the weighted average classification loss.
n is the sample size.
For binary classification:
yj is the observed class label. The software codes it as –1 or 1, indicating the negative or positive class (or the first or second class in the
ClassNamesproperty), respectively.f(Xj) is the positive-class classification score for observation (row) j of the predictor data X.
mj = yjf(Xj) is the classification score for classifying observation j into the class corresponding to yj. Positive values of mj indicate correct classification and do not contribute much to the average loss. Negative values of mj indicate incorrect classification and contribute significantly to the average loss.
For algorithms that support multiclass classification (that is, K ≥ 3):
yj* is a vector of K – 1 zeros, with 1 in the position corresponding to the true, observed class yj. For example, if the true class of the second observation is the third class and K = 4, then y2* = [
0 0 1 0]′. The order of the classes corresponds to the order in theClassNamesproperty of the input model.f(Xj) is the length K vector of class scores for observation j of the predictor data X. The order of the scores corresponds to the order of the classes in the
ClassNamesproperty of the input model.mj = yj*′f(Xj). Therefore, mj is the scalar classification score that the model predicts for the true, observed class.
The weight for observation j is wj. The software normalizes the observation weights so that they sum to the corresponding prior class probability stored in the
Priorproperty. Therefore,
Given this scenario, the following table describes the supported loss functions that you can specify by using the LossFun name-value argument.
| Loss Function | Value of LossFun | Equation |
|---|---|---|
| Binomial deviance | "binodeviance" | |
| Observed misclassification cost | "classifcost" | where is the class label corresponding to the class with the maximal score, and is the user-specified cost of classifying an observation into class when its true class is yj. |
| Misclassified rate in decimal | "classiferror" | where I{·} is the indicator function. |
| Cross-entropy loss | "crossentropy" |
The weighted cross-entropy loss is where the weights are normalized to sum to n instead of 1. |
| Exponential loss | "exponential" | |
| Hinge loss | "hinge" | |
| Logistic loss | "logit" | |
| Minimal expected misclassification cost | "mincost" |
The software computes the weighted minimal expected classification cost using this procedure for observations j = 1,...,n.
The weighted average of the minimal expected misclassification cost loss is |
| Quadratic loss | "quadratic" |
If you use the default cost matrix (whose element value is 0 for correct classification
and 1 for incorrect classification), then the loss values for
"classifcost", "classiferror", and
"mincost" are identical. For a model with a nondefault cost matrix,
the "classifcost" loss is equivalent to the "mincost"
loss most of the time. These losses can be different if prediction into the class with
maximal posterior probability is different from prediction into the class with minimal
expected cost. Note that "mincost" is appropriate only if classification
scores are posterior probabilities.
This figure compares the loss functions (except "classifcost",
"crossentropy", and "mincost") over the score
m for one observation. Some functions are normalized to pass through
the point (0,1).

Algorithms
For each conditional predictor distribution, loss computes the weighted average and standard deviation.
If the prior class probability distribution is known (in other words, the prior distribution is not empirical), loss normalizes observation weights to sum to the prior class probabilities in the respective classes. This action implies that the default observation weights are the respective prior class probabilities.
If the prior class probability distribution is empirical, the software normalizes the specified observation weights to sum to 1 each time you call loss.
Version History
Introduced in R2021a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)