gammaln

Logarithmic gamma function

Syntax

gammaln(X)

Description

gammaln(X) returns the logarithmic gamma function for each element of X.

Examples

Logarithmic Gamma Function for Numeric and Symbolic Arguments

Depending on its arguments, gammaln returns floating-point or exact symbolic results.

Compute the logarithmic gamma function for these numbers. Because these numbers are not symbolic objects, you get floating-point results.

A = gammaln([1/5, 1/2, 2/3, 8/7, 3])

A =
    1.5241    0.5724    0.3032   -0.0667    0.6931

Compute the logarithmic gamma function for the numbers converted to symbolic objects. For many symbolic (exact) numbers, gammaln returns results in terms of the gammaln, log, and gamma functions.

symA = gammaln(sym([1/5, 1/2, 2/3, 8/7, 3]))

symA =
[ gammaln(1/5), log(pi^(1/2)), gammaln(2/3),...
log(gamma(1/7)/7), log(2)]

Use vpa to approximate symbolic results with floating-point numbers:

vpa(symA)

ans =
[ 1.5240638224307845248810564939263,...
0.57236494292470008707171367567653,...
0.30315027514752356867586281737201,...
-0.066740877459477468649396334098109,...
0.69314718055994530941723212145818]

Definition of the Logarithmic Gamma Function on Complex Plane

gammaln is defined for all complex arguments, except negative infinity.

Compute the logarithmic gamma function for positive integer arguments. For such arguments, the logarithmic gamma function is defined as the natural logarithm of the gamma function, gammaln(x) = log(gamma(x)).

pos = gammaln(sym([1/4, 1/3, 1, 5, Inf]))

pos =
[ log((pi*2^(1/2))/gamma(3/4)), log((2*pi*3^(1/2))/(3*gamma(2/3))), 0, log(24), Inf]

Compute the logarithmic gamma function for nonpositive integer arguments. For nonpositive integers, gammaln returns Inf.

nonposint = gammaln(sym([0, -1, -2, -5, -10]))

nonposint =
[ Inf, Inf, Inf, Inf, Inf]

Compute the logarithmic gamma function for complex and negative rational arguments. For these arguments, gammaln returns unresolved symbolic calls.

complex = gammaln(sym([i, -1 + 2*i , -2/3, -10/3]))

complex =
[ gammaln(1i), gammaln(- 1 + 2i), gammaln(-2/3), gammaln(-10/3)]

Use vpa to approximate symbolic results with floating-point numbers:

vpa(complex)

ans =
[ - 0.65092319930185633888521683150395 - 1.8724366472624298171188533494366i,...
- 3.3739449232079248379476073664725 - 3.4755939462808110432931921583558i,...
1.3908857550359314511651871524423 - 3.1415926535897932384626433832795i,...
- 0.93719017334928727370096467598178 - 12.566370614359172953850573533118i]

Compute the logarithmic gamma function of negative infinity:

gammaln(sym(-Inf))

ans =
NaN

Plot Logarithmic Gamma Function

Plot the logarithmic gamma function on the interval from 0 to 10.

syms x
fplot(gammaln(x),[0 10])
grid on

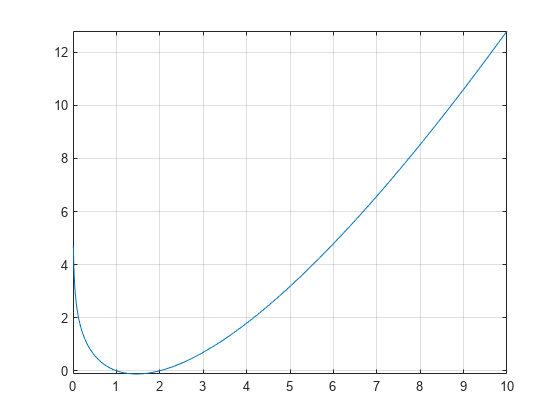
To see the negative values better, plot the same function on the interval from 1 to 2.

fplot(gammaln(x),[1 2])
grid on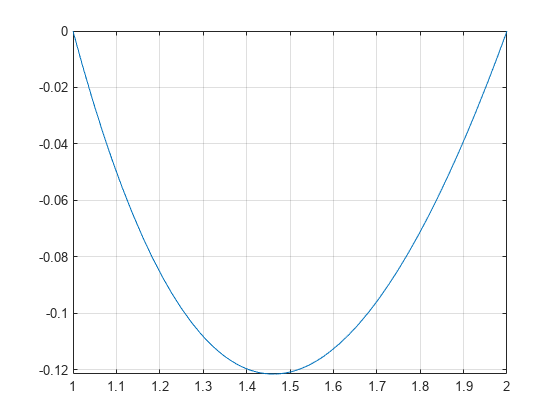

Handle Expressions Containing Logarithmic Gamma Function

Many functions, such as diff and limit, can handle expressions containing lngamma.

Differentiate the logarithmic gamma function:

syms x
diff(gammaln(x), x)

ans =
psi(x)

Compute the limits of these expressions containing the logarithmic gamma function:

syms x
limit(1/gammaln(x), x, Inf)

ans =
0

limit(gammaln(x - 1) - gammaln(x - 2), x, 0)

ans =
log(2) + pi*1i

Input Arguments

X — Input

symbolic number | symbolic variable | symbolic expression | symbolic function | symbolic vector | symbolic matrix

Input, specified as symbolic number, variable, expression, function, or as a vector or matrix of symbolic numbers, variables, expressions, or functions.

Algorithms

For single or double input to gammaln(x), x must be real and positive.

For symbolic input,

• gammaln(x) is defined for all complex x except the singular points 0, -1, -2, ... .

• For positive real x, gammaln(x) represents the logarithmic gamma function log(gamma(x)).

• For negative real x or for complex x, gammaln(x) = log(gamma(x)) + f(x)2πi where f(x) is some integer valued function. The integer multiples of 2πi are chosen such that gammaln(x) is analytic throughout the complex plane with a branch cut along the negative real semi axis.

• For negative real x, gammaln(x) is equal to the limit of log(gamma(x)) from ‘above’.