mlpt
Multiscale local 1-D polynomial transform
Syntax
Description
[ returns
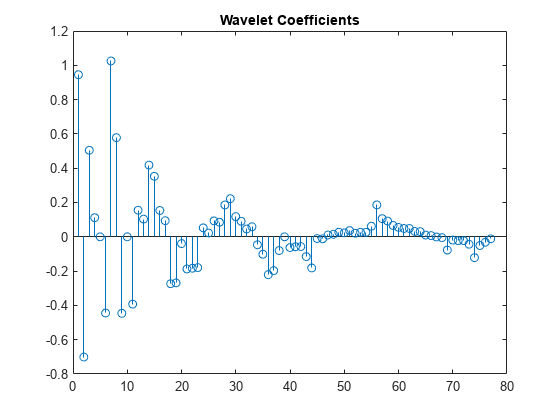
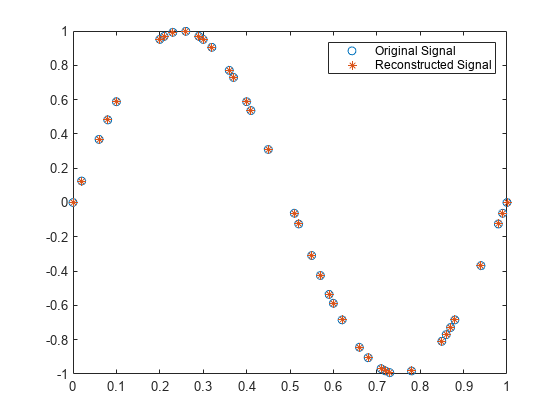
the multiscale local polynomial 1-D transform (MLPT) of input signal coefs,T,coefsPerLevel,scalingMoments]
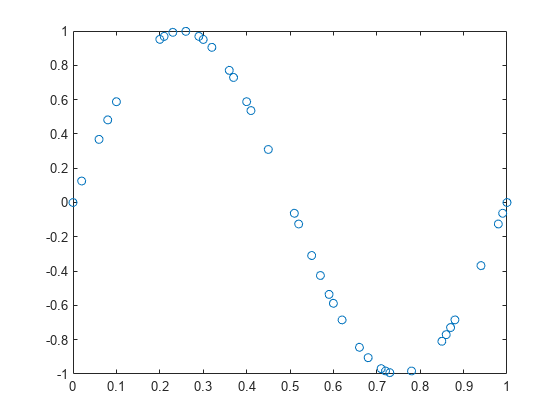
= mlpt(x,t)x sampled
at the sampling instants, t. If x or t contain NaNs,
the union of the NaNs in x and t is
removed before obtaining the mlpt.
[ returns
the transform for coefs,T,coefsPerLevel,scalingMoments]
= mlpt(x,t,numLevel)numLevel resolution levels.
[ uses uniform sampling instants
for coefs,T,coefsPerLevel,scalingMoments]
= mlpt(x)x as the time instants if x does
not contain NaNs. If x contains NaNs,
the NaNs are removed from x and
the nonuniform sampling instants are obtained from the numeric elements
of x.
[ specifies coefs,T,coefsPerLevel,scalingMoments]
= mlpt(___,Name,Value)mlpt properties
using one or more Name,Value pair arguments and
any of the previous input arguments.
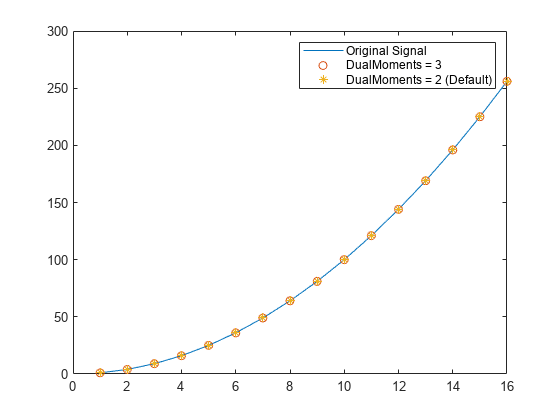
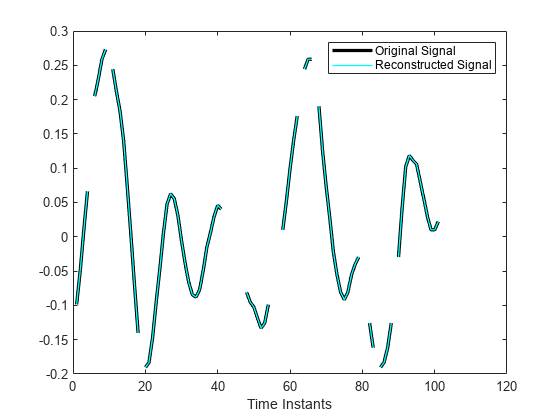
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
Maarten Jansen developed the theoretical foundation of the multiscale
local polynomial transform (MLPT) and algorithms for its efficient
computation [1][2][3]. The MLPT uses a lifting scheme, wherein a kernel
function smooths fine-scale coefficients with a given bandwidth to
obtain the coarser resolution coefficients. The mlpt function uses only local polynomial
interpolation, but the technique developed by Jansen is more general
and admits many other kernel types with adjustable bandwidths [2].
References
[1] Jansen, Maarten. “Multiscale Local Polynomial Smoothing in a Lifted Pyramid for Non-Equispaced Data.” IEEE Transactions on Signal Processing 61, no. 3 (February 2013): 545–55. https://doi.org/10.1109/TSP.2012.2225059.
[2] Jansen, Maarten, and Mohamed Amghar. “Multiscale Local Polynomial Decompositions Using Bandwidths as Scales.” Statistics and Computing 27, no. 5 (September 2017): 1383–99. https://doi.org/10.1007/s11222-016-9692-8.
[3] Jansen, Maarten, and Patrick Oonincx. Second Generation Wavelets and Applications. London ; New York: Springer, 2005.
Version History
Introduced in R2017a