Radial Basis Function Neural Networks (with parameter selection using K-means)
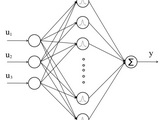
A RBFNN is an artificial neural network that uses radial basis functions as activation functions. Figure shows the structure of the RBFNN. The RBFNN is three layered feed-forward neural network. The first layer is linear and only distributes the input signal, while the next layer is nonlinear and uses Gaussian functions. The third layer linearly combines the Gaussian outputs. Only the tap weights between the hidden layer and the output layer are modified during training.
RBFNN have 5 parameters for optimization:
1- The weights between the hidden layer and the output layer.
2- The activation function.
3- The center of activation functions.
4- The distribution of center of activation functions.
5- The number of hidden neurons.
The weights between the hidden layer and the output layer are calculated by using Moore-Penrose generalized pseudo-inverse. This algorithm overcomes many issues in traditional gradient algorithms such as stopping criterion, learning rate, number of epochs and local minima. Due to its shorter training time and generalization ability, it is suitable for real-time applications.
The radial basis function selected is usually a Gaussian kernel for pattern recognition application.
Generally the center and distribution of activation functions should have characteristic similar to data. Here, the center and width of Gaussians are selected using Kmeans clustering algorithm.
Based on universal approximation theory center and distribution of activation functions are not deterministic if the numbers of hidden neurons being sufficient enough, one can say that the single hidden layer feed-forward network with sufficient number of hidden neurons can approximate any function to any arbitrary level of accuracy.
---------------------------------------------------------------------------------
This code is used in the following papers:
1. A. Asvadi, M. Karami, Y. Baleghi, “Efficient Object Tracking Using Optimized K-means Segmentation and Radial Basis Function Neural Networks,” International Journal of Information and Communication Technology Research (IJICT), vol. 4, no. 1, pp. 29-39, December 2011.
2. A. Asvadi, M. Karami, Y. Baleghi, H. Seyyedi, “Improved Object Tracking Using Radial Basis Function Neural Networks,” in: Proceedings of 7th Iranian Machine Vision and Image Processing (MVIP2011), Tehran, Iran, November 2011.
---------------------------------------------------------------------------------
"mvnrnd" from "Statistics and Machine Learning Toolbox" is used for generating sample data points.
Citar como
Alireza (2024). Radial Basis Function Neural Networks (with parameter selection using K-means) (https://www.mathworks.com/matlabcentral/fileexchange/52580-radial-basis-function-neural-networks-with-parameter-selection-using-k-means), MATLAB Central File Exchange. Recuperado .
Compatibilidad con la versión de MATLAB
Compatibilidad con las plataformas
Windows macOS LinuxCategorías
- AI, Data Science, and Statistics > Deep Learning Toolbox > Function Approximation, Clustering, and Control > Function Approximation and Clustering >
- AI, Data Science, and Statistics > Deep Learning Toolbox > Image Data Workflows > Pattern Recognition and Classification >
Etiquetas
Agradecimientos
Inspirado por: K-means clustering
Inspiración para: KM-RBF Tracker, RBF Neural Networks with random selection of parameters
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Descubra Live Editor
Cree scripts con código, salida y texto formateado en un documento ejecutable.
RBFNs/
| Versión | Publicado | Notas de la versión | |
|---|---|---|---|
| 1.0.0.0 | Image added
Description added
|