Matrix Methods of Linear Algebra
Matrix Methods of Linear Algebra
Curriculum Module
Created with R2020b. Compatible with R2020b and later releases.
Information
This curriculum module contains interactive MATLAB® live scripts that teach fundamental matrix methods commonly taught in introductory linear algebra courses. In the first part of each live script, students learn standard definitions, visualize concepts, and perform exercises on paper. Afterward, students practice complementary MATLAB® methods. These methods reinforce the discussed concepts and help students to develop an early familiarity with computational software. Each lesson concludes with an illustrative application.
Background
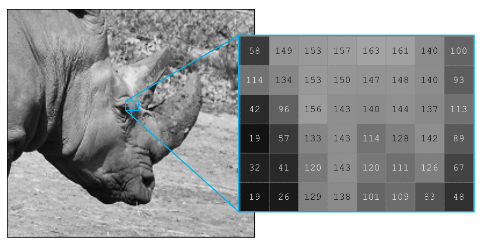
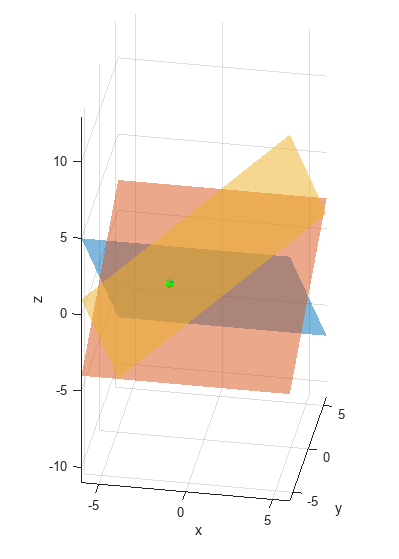
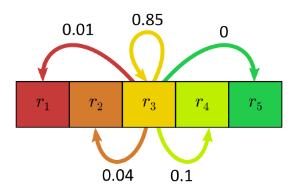
You can use these live scripts as demonstrations in lectures, class activities, or interactive assignments outside class. This module covers topics such as matrix operations, linear systems, determinants, eigenvalues and eigenvectors, and diagonalization. It also includes examples of using matrix methods to modify grayscale images, analyze linear circuits, understanding vibrations, and Markov chains.
The instructions inside the live scripts will guide you through the exercises and activities. Get started with each live script by running it one section at a time. To stop running the script or a section midway (for example, when an animation is in progress), use the ![]() Stop button in the RUN section of the Live Editor tab in the MATLAB Toolstrip.
Stop button in the RUN section of the Live Editor tab in the MATLAB Toolstrip.
Contact Us
Solutions are available upon instructor request. Contact the MathWorks teaching resources team if you would like to request solutions, provide feedback, or if you have a question.
Getting Started
Accessing the Module
On MATLAB Online:
Use the  link to download the module. You will be prompted to log in or create a MathWorks account. The project will be loaded, and you will see an app with several navigation options to get you started.
link to download the module. You will be prompted to log in or create a MathWorks account. The project will be loaded, and you will see an app with several navigation options to get you started.
On Desktop:
Download or clone this repository. Open MATLAB, navigate to the folder containing these scripts and double-click on MatrixMethods.prj. It will add the appropriate files to your MATLAB path and open an app that asks you where you would like to start.
Ensure you have all the required products (listed below) installed. If you need to include a product, add it using the Add-On Explorer. To install an add-on, go to the Home tab and select ![]() Add-Ons > Get Add-Ons.
Add-Ons > Get Add-Ons.
Products
MATLAB® is used throughout. Tools from Symbolic Math Toolbox™, Statistics and Machine Learning Toolbox™, and Image Processing Toolbox™ are used as well.
Scripts
If you are viewing this in a version of MATLAB prior to R2023b, you can view the learning outcomes for each script here
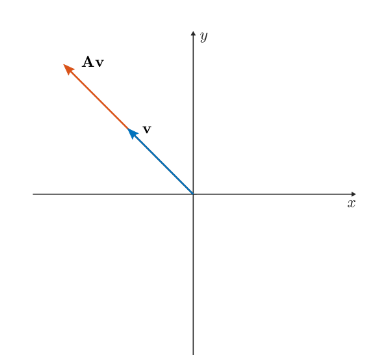
MatrixOperations.mlx
LinearSystems.mlx
LinearSystemsApplications.mlx
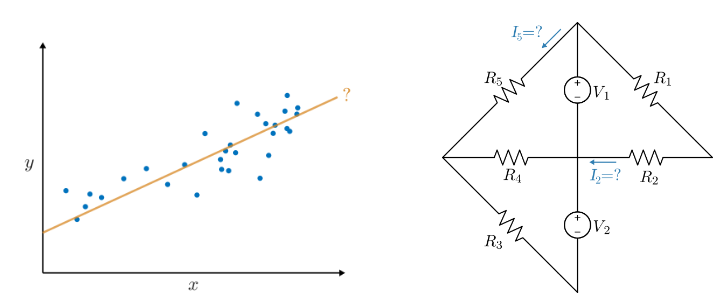 |
In this script, students will... - Apply matrix methods to linear regression and linear circuit analysis |
Academic disciplines - Linear algebra - Statistical analysis - Circuit analysis |
|---|
Eigenanalysis.mlx
EigenanalysisApplications.mlx
Related Courseware Modules
Vector Arithmetic
 |
Available on:  GitHub GitHub
|
|---|
Applied Linear Algebra
 |
Available on:  GitHub GitHub
|
|---|
Or feel free to explore our other modular courseware content.
Educator Resources
Contribute
Looking for more? Find an issue? Have a suggestion? Please contact the MathWorks teaching resources team. If you want to contribute directly to this project, you can find information about how to do so in the CONTRIBUTING.md page on GitHub.
© Copyright 2023 The MathWorks™, Inc
Citar como
Ryan Weinstein (2024). Matrix Methods of Linear Algebra (https://github.com/MathWorks-Teaching-Resources/Matrix-Methods-of-Linear-Algebra/releases/tag/v1.1.0), GitHub. Recuperado .
Compatibilidad con la versión de MATLAB
Compatibilidad con las plataformas
Windows macOS LinuxEtiquetas
Comunidades de usuarios
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Descubra Live Editor
Cree scripts con código, salida y texto formateado en un documento ejecutable.
SoftwareTests
Utilities
Scripts
| Versión | Publicado | Notas de la versión | |
|---|---|---|---|
| 1.1.0.0 | See release notes for this release on GitHub: https://github.com/MathWorks-Teaching-Resources/Matrix-Methods-of-Linear-Algebra/releases/tag/v1.1.0 |
||
| 1.0.5.0 | See release notes for this release on GitHub: https://github.com/MathWorks-Teaching-Resources/Matrix-Methods-of-Linear-Algebra/releases/tag/v1.0.5 |
||
| 1.0.4.0 | See release notes for this release on GitHub: https://github.com/MathWorks-Teaching-Resources/Matrix-Methods-of-Linear-Algebra/releases/tag/v1.0.4 |
||
| 1.0.3 | See release notes for this release on GitHub: https://github.com/MathWorks-Teaching-Resources/Matrix-Methods-of-Linear-Algebra/releases/tag/v1.0.3 |
||
| 1.0.2 | See release notes for this release on GitHub: https://github.com/MathWorks-Teaching-Resources/Matrix-Methods-of-Linear-Algebra/releases/tag/v1.0.2 |
||
| 1.0.1 | See release notes for this release on GitHub: https://github.com/MathWorks-Teaching-Resources/Matrix-Methods-of-Linear-Algebra/releases/tag/v1.0.1 |
||
| 1.0.0 |