series

Conexión en serie de dos modelos

contraer todo en la página

Sintaxis

sys = series(sys1,sys2)
sys = series(sys1,sys2,out1,in2)
sys = series(sys1,sys2,"name")

Descripción

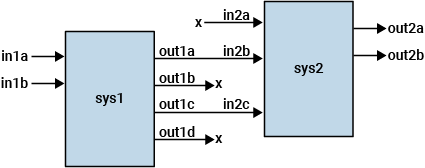
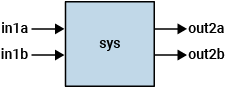
sys = series(sys1,sys2) establece la interconexión en serie de dos modelos de sistemas dinámicos al conectar las salidas de sys1 a las entradas de sys2, tal como se muestra en el diagrama.

Este comando equivale a la multiplicación directa sys = sys2*sys1. En los sistemas MIMO, el número de entradas de sys2 debe ser igual al número de salidas de sys1. El sys resultante tiene entradas u y salidas y.

ejemplo

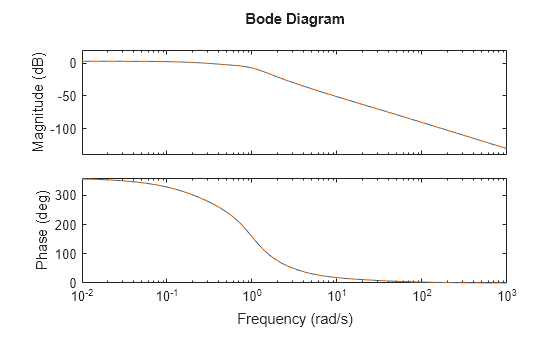
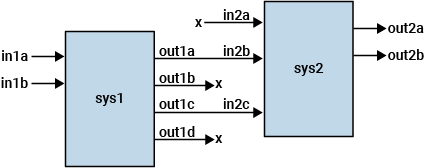
sys = series(sys1,sys2,out1,in2) establece la interconexión en serie más general que se muestra en el siguiente diagrama al conectar un subconjunto de las salidas de sys1 a un subconjunto de las entradas de sys2.

out1 es un vector que especifica los índices de las salidas de sys1 que desea conectar. Del mismo modo, in1 especifica los índices de las entradas de sys2 que desea conectar a esas salidas. El sys resultante tiene entradas u y salidas y. series elimina las salidas no conectadas z1 de sys1 y las entradas no conectadas v2 de sys2.

ejemplo

sys = series(sys1,sys2,"name") conecta un subconjunto de las salidas de sys1 a un subconjunto de las entradas de sys2 haciendo coincidir los nombres de las señales definidos en las propiedades OutputName e InputName de los modelos. series elimina las salidas no conectadas de sys1 y las entradas no conectadas de sys2.

ejemplo

Ejemplos

contraer todo

Abrir script en vivo

Cree dos sistemas SISO, siendo uno de ellos un modelo de espacio de estados y el otro una función de transferencia.

sys1 = rss(3);
sys2 = tf(1,[1 1 1]);

Realice la conexión en serie de los dos sistemas.

sys = series(sys1,sys2);
size(sys)
State-space model with 1 outputs, 1 inputs, and 5 states.

Al conectar una función de transferencia con un modelo de espacio de estados se obtiene otro modelo de espacio de estados. Para obtener más información sobre los resultados de combinar distintos tipos de modelos, consulte Rules That Determine Model Type.

La interconexión en serie equivale al producto de sys2*sys1. Compruebe esta equivalencia examinando las respuestas en frecuencia. 

sysm = sys2*sys1;
bodeplot(sys,'-',sysm,'--')

MATLAB figure

Abrir script en vivo

Conecte dos sistemas MIMO en serie. Cuando el número de salidas de sys1 es igual al número de entradas de sys2, puede conectar todas las salidas de sys1 a todas las entradas de sys2. 

sys1 = rss(3,2,3);
sys2 = rss(3,3,2);
sys = series(sys1,sys2);

El sistema resultante tiene el mismo número de entradas que sys1 y el mismo número de salidas que sys2.

size(sys)
State-space model with 3 outputs, 3 inputs, and 6 states.
Abrir script en vivo

Puede establecer conexiones en serie asignando nombres que coincidan con las señales que desea conectar. Partiendo del sistema de cuatro salidas y dos entradas sys1 y del sistema de dos salidas y tres entradas sys2, establezca la conexión en serie que se muestra en el diagrama.

Cree modelos de espacio de estados de los dos sistemas y asigne un nombre a las señales de entrada y salida. 

% sys1: 4-output, 2-input
sys1 = rss(4,4,2);
sys1.InputName = ["in1a","in1b"];
sys1.OutputName = ["out1a","out1b","out1c","out1d"];
% sys2: 2-output, 3-input
sys2 = rss(3,2,3);
sys2.InputName = ["in2a","in2b","in2c"];
sys2.OutputName = ["out2a","out2b"];

En la interconexión que se muestra en el diagrama, out1a y out1c de sys1 se conectan a in2b e in2c, respectivamente. Cambie los nombres de las señales para que coincidan los nombres de las señales de conexión.

sys1.OutputName = ["ua","out1b","ub","out1d"];
sys2.InputName = ["in2a","ua","ub"];

Establezca la conexión llamando a series con el indicador name.

sys = series(sys1,sys2,"name");

Examine las dimensiones, entradas y salidas de sys para confirmar que las conexiones coinciden con las del diagrama. 

size(sys)
State-space model with 2 outputs, 2 inputs, and 7 states.

sys.InputName
ans = 2×1 cell
    {'in1a'}
    {'in1b'}


sys.OutputName
ans = 2×1 cell
    {'out2a'}
    {'out2b'}

Como se esperaba, el modelo sys resultante tiene dos salidas y dos entradas, que corresponden a las salidas de sys2 y a las entradas de sys1, respectivamente.

sys elimina las entradas no conectadas de sys2 y las salidas no conectadas de sys1. Para establecer esta interconexión y conservar todas las entradas y salidas, use connect y especifique todas las entradas y salidas que desea conservar en el sistema resultante.

sysc = connect(sys1,sys2,["in1a","in1b","in2a"],["out2a","out2b","out1b","out1d"]);
size(sysc)
State-space model with 4 outputs, 3 inputs, and 7 states.

sysc.InputName
ans = 3×1 cell
    {'in1a'}
    {'in1b'}
    {'in2a'}


sysc.OutputName
ans = 4×1 cell
    {'out2a'}
    {'out2b'}
    {'out1b'}
    {'out1d'}
Abrir script en vivo

Puede establecer interconexiones en serie con un subconjunto de entradas y salidas del modelo especificando los índices de las señales que desea conectar. Partiendo del sistema de cuatro salidas y dos entradas sys1 y del sistema de dos salidas y tres entradas sys2, establezca la conexión en serie que se muestra en el diagrama.

Cree modelos de espacio de estados de los dos sistemas. 

% sys1: 4-output, 2-input
sys1 = rss(4,4,2);
% sys2: 2-output, 3-input
sys2 = rss(3,2,3);

Para establecer la conexión en serie, cree vectores que especifiquen las salidas de sys1 y las entradas correspondientes de sys2 que desea conectar. En el diagrama, la primera y la tercera salida de sys1 se conectan a la segunda y la tercera entrada de sys2, respectivamente. Por lo tanto, especifique los índices de la siguiente manera.

out1 = [1 3]; % out1a and out1c
in2 = [2 3];  % in2b and in2c

Establezca la conexión y examine el tamaño de la salida.

sys = series(sys1,sys2,out1,in2);
size(sys)
State-space model with 2 outputs, 2 inputs, and 7 states.

Como se esperaba, el modelo sys resultante tiene dos salidas y dos entradas, que corresponden a las salidas de sys2 y a las entradas de sys1, respectivamente. sys elimina las entradas no conectadas de sys2 y las salidas no conectadas de sys1. Para establecer esta interconexión y conservar todas las entradas y salidas, utilice connect.

Argumentos de entrada

contraer todo

Sistemas que desea conectar, especificados como un modelo de sistema dinámico SISO o MIMO, un bloque de diseño de control o un arreglo de modelos de sistemas dinámicos. Entre los modelos y bloques que se pueden conectar, se incluyen los siguientes:

  • Cualquier objeto de modelo LTI numérico, como un objeto de modelo tf, zpk, ss, frd o pid.

  • Un modelo LTI generalizado o con incertidumbre, como un modelo genss, genfrd, uss (Robust Control Toolbox) y ufrd (Robust Control Toolbox).

  • Un bloque de diseño de control que representa un elemento de diagrama de bloques ajustable o con incertidumbre, como un bloque tunablePID, tunableSS, tunableGain, tunableTF, tunableSurface, ultidyn (Robust Control Toolbox) o umargin (Robust Control Toolbox).

  • Un bloque AnalysisPoint que representa una ubicación en el diagrama de bloques donde desea extraer las respuestas del sistema.

  • Una unión de suma que se crea con sumblk.

  • Un modelo LTI identificado, como un modelo idtf (System Identification Toolbox), idss (System Identification Toolbox) o idproc (System Identification Toolbox).

  • Un modelo disperso, representado por un objeto de modelo sparss o mechss.

  • Un modelo variante en el tiempo o de parámetros variantes, representado por un objeto de modelo ltvss o lpvss.

sys1 y sys2 deben ser ambos continuos o ambos discretos con el mismo tiempo de muestreo.

Salidas de sys1 que desea conectar, especificadas como un vector de índices. Por ejemplo, si desea conectar la segunda, cuarta y quinta salidas de sys1 a tres entradas de sys2, establezca out1 = [2,4,5].

Entradas de sys2 que desea conectar, especificadas como un vector de índices. Por ejemplo, si desea conectar tres salidas de sys1 a la primera, tercera y cuarta entradas de sys2, establezca in2 = [1,3,4].

Argumentos de salida

contraer todo

Sistema interconectado, devuelto como modelo de sistema dinámico cuyas entradas son las entradas de sys1 y cuyas salidas son las salidas de sys2. El tipo de modelo de sistema dinámico depende de los tipos de sistemas conectados sys1 y sys2. Por ejemplo,

  • Si uno de los sistemas conectados es un modelo ss y el otro es un modelo LTI numérico distinto de un modelo frd, sys es un modelo ss.

  • Si uno de los sistemas conectados es un modelo frd y el otro es un modelo LTI numérico, sys es un modelo frd. Si ambos sistemas son modelos frd, los vectores de frecuencia deben coincidir.

  • Si uno de los sistemas conectados es un modelo LTI identificado, sys también es un modelo identificado.

  • Si uno de los sistemas conectados es un modelo LTI generalizado, como un modelo genss o uss, sys también es un modelo LTI generalizado.

  • Si uno de los sistemas conectados es un modelo disperso, sys es también un modelo disperso.

Si sys1 y sys2 son arreglos de modelos, sys es un arreglo de modelos del mismo tamaño. Cada entrada de sys es el modelo formado por la conexión de las entradas correspondientes de los arreglos de entrada.

Historial de versiones

Introducido antes de R2006a

Consulte también

| | |