La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

parallel

Conexión paralela de dos modelos

contraer todo en la página

    Sintaxis

    sys = parallel(sys1,sys2)
    sys = parallel(sys1,sys2,in1,in2,out1,out2)
    sys = parallel(sys1,sys2,"name")

    Descripción

    sys = parallel(sys1,sys2) establece la interconexión en paralelo de dos modelos de sistemas dinámicos conectando las mismas señales de entrada a sys1 y sys2 y sumando las salidas, tal como se muestra en el diagrama.

    Este comando equivale a la multiplicación directa sys = sys1 + sys2. En el caso de los sistemas MIMO, sys2 y sys2 deben tener el mismo número de entradas y salidas.

    ejemplo

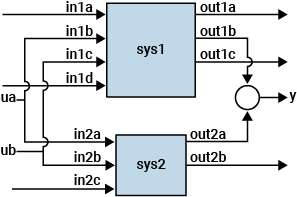
    sys = parallel(sys1,sys2,in1,in2,out1,out2) forma la interconexión paralela más general que se muestra en el siguiente diagrama.

    Los vectores in1 e 1n2 contienen índices a las entradas de sys1 y sys2 que reciben las entradas u. Del mismo modo, out1 y out2 son vectores que especifican las salidas de sys1 y sys2, que se suman para formar las salidas y. El sys resultante tiene entradas [v1,u,v2], donde v1 y v2 son las entradas no especificadas en in1 e 1n2. Del mismo modo, sys tiene salidas [z1,y,z2], donde z1 y z2 son las salidas no especificadas en out1 y out2.

    ejemplo

    sys = parallel(sys1,sys2,"name") conecta un sys1 y un sys2 al hacer coincidir los nombres de las señales definidos en las propiedades OutputName y InputName de los modelos. Las entradas cuyos nombres coinciden se conectan y las salidas cuyos nombres coinciden se suman.

    ejemplo

    Ejemplos

    contraer todo

    Abrir script en vivo

    Cree dos sistemas SISO, siendo uno de ellos un modelo de espacio de estados y el otro una función de transferencia.

    sys1 = rss(3);
sys2 = tf(1,[1 1 1]);

    Forme la interconexión en paralelo de los dos sistemas y examine el modelo resultante. 

    sys = parallel(sys1,sys2);
size(sys)
    State-space model with 1 outputs, 1 inputs, and 5 states.

    Al conectar una función de transferencia con un modelo de espacio de estados se obtiene otro modelo de espacio de estados. Para obtener más información sobre los resultados de combinar distintos tipos de modelos, consulte Rules That Determine Model Type.

    La interconexión en paralelo equivale a la suma aritmética de los dos modelos. Compruebe esta equivalencia examinando las respuestas en frecuencia. 

    sysa = sys1 + sys2;
bodeplot(sys,'-',sysa,'--')

    MATLAB figure

    Abrir script en vivo

    Conecte dos sistemas MIMO en paralelo. Cuando los dos sistemas tienen las mismas dimensiones de entrada-salida, se pueden conectar todas las entradas y salidas. Por ejemplo, cree dos sistemas de tres salidas y dos entradas, y forme esta interconexión. 

    sys1 = rss(4,3,2);
sys2 = rss(4,3,2);
sys = parallel(sys1,sys2);

    El modelo resultante tiene las mismas dimensiones de entrada-salida.

    size(sys)
    State-space model with 3 outputs, 2 inputs, and 8 states.
    Abrir script en vivo

    Puede establecer conexiones en paralelo asignando nombres que coincidan con las señales que desea conectar. Partiendo del sistema de tres salidas y cuatro entradas sys1 y del sistema de dos salidas y tres entradas sys2, forme la conexión en paralelo que se muestra en el diagrama.

    Cree modelos de espacio de estados de los dos sistemas y asigne un nombre a las señales de entrada y salida. 

    % sys1: 3-output, 4-input
sys1 = rss(4,3,4);
sys1.InputName = ["in1a","in1b","in1c","in1d"];
sys1.OutputName = ["out1a","out1b","out1c"];
% sys2: 2-output, 3-input
sys2 = rss(3,2,3);
sys2.InputName = ["in2a","in2b","in2c"];
sys2.OutputName = ["out2a","out2b"];

    En la interconexión que se muestra en el diagrama, las entradas 2 y 3 de sys1 se conectan a las entradas 1 y 2 de sys2, respectivamente. El diagrama también muestra que la segunda salida de sys1 se suma a la primera salida de sys2. Cambie los nombres de las señales para que coincidan los nombres de las señales de conexión.

    sys1.InputName = ["in1a","u1","u2","in1d"];
sys1.OutputName = ["out1a","y1","out1c"];
sys2.InputName = ["u1","u2","in2c"];
sys2.OutputName = ["y1","out2b"];

    Establezca la conexión usando el indicador name. 

    sys = parallel(sys1,sys2,"name");

    Examine las dimensiones, entradas y salidas de sys para confirmar que las conexiones coinciden con las del diagrama. 

    size(sys)
    State-space model with 4 outputs, 5 inputs, and 7 states.

    sys.InputName
    ans = 5×1 cell
    {'in1a'}
    {'in1d'}
    {'u1'  }
    {'u2'  }
    {'in2c'}


    sys.OutputName
    ans = 4×1 cell
    {'out1a'}
    {'out1c'}
    {'y1'   }
    {'out2b'}
    Abrir script en vivo

    Puede establecer interconexiones en paralelo con un subconjunto de entradas y salidas del modelo especificando los índices de las señales que desea conectar. Partiendo del sistema de tres salidas y cuatro entradas sys1 y del sistema de dos salidas y tres entradas sys2, forme la conexión en paralelo que se muestra en el diagrama.

    Cree modelos de espacio de estados de los dos sistemas. 

    % sys1: 3-output, 4-input
sys1 = rss(4,3,4);
% sys2: 2-output, 3-input
sys2 = rss(3,2,3);

    Para establecer la interconexión, cree vectores que especifiquen las entradas y salidas de cada modelo que desea conectar. Por ejemplo, tal y como se muestra en el diagrama, las entradas 2 y 3 de sys1 se conectan a las entradas 1 y 2 de sys2, respectivamente. Por lo tanto, especifique los índices de entrada de la siguiente manera. 

    inp1 = [2 3];  % indices of in1b and in1c
inp2 = [1 2];  % indices of in2a and in2b

    El diagrama también muestra que la segunda salida de sys1 se suma a la primera salida de sys2. 

    out1 = [2];  % index of out1b
out2 = [1];  % index of out2a

    Use estos valores para establecer la interconexión en paralelo. 

    sys = parallel(sys1,sys2,inp1,inp2,out1,out2);

    El modelo resultante tiene cuatro salidas y cinco entradas, como se esperaba.

    size(sys)
    State-space model with 4 outputs, 5 inputs, and 7 states.

    Argumentos de entrada

    contraer todo

    Sistemas que desea conectar, especificados como un modelo de sistema dinámico SISO o MIMO, un bloque de diseño de control o un arreglo de modelos de sistemas dinámicos. Entre los modelos y bloques que se pueden conectar, se incluyen los siguientes:

    • Cualquier objeto de modelo LTI numérico, como un objeto de modelo tf, zpk, ss, frd o pid.

    • Un modelo LTI generalizado o con incertidumbre, como un modelo genss, genfrd, uss (Robust Control Toolbox) y ufrd (Robust Control Toolbox).

    • Un bloque de diseño de control que representa un elemento de diagrama de bloques ajustable o con incertidumbre, como un bloque tunablePID, tunableSS, tunableGain, tunableTF, tunableSurface, ultidyn (Robust Control Toolbox) o umargin (Robust Control Toolbox).

    • Un bloque AnalysisPoint que representa una ubicación en el diagrama de bloques donde desea extraer las respuestas del sistema.

    • Una unión de suma que se crea con sumblk.

    • Un modelo LTI identificado, como un modelo idtf (System Identification Toolbox), idss (System Identification Toolbox) o idproc (System Identification Toolbox).

    • Un modelo disperso, representado por un objeto de modelo sparss o mechss.

    • Un modelo variante en el tiempo o de parámetros variantes, representado por un objeto de modelo ltvss o lpvss.

    sys1 y sys2 deben ser ambos continuos o ambos discretos con el mismo tiempo de muestreo.

    Entradas de sys1 y sys2 que se van a conectar, especificadas como vectores de índices. Por ejemplo, si desea enviar la misma entrada a la primera entrada de sys1 y a la segunda entrada de sys2, la segunda entrada de sys1 y la tercera entrada de sys2 y la tercera entrada de sys1 y la quinta entrada de sys2, establezca in2 = [1,2,3] e in2 = [2,3,5].

    Salidas de sys1 y sys2 que se van a sumar, especificadas como un vector de índices. Por ejemplo, si desea sumar la primera salida de sys1 con la segunda salida de sys2, la segunda salida de sys1 con la tercera salida de sys2 y la tercera salida de sys1 con la quinta salida de sys2, establezca in2 = [1,2,3] e in2 = [2,3,5].

    Argumentos de salida

    contraer todo

    Sistema interconectado, devuelto como modelo de sistema dinámico. El tipo de modelo de sistema dinámico depende de los tipos de sistemas conectados sys1 y sys2. Por ejemplo,

    • Si uno de los sistemas conectados es un modelo ss y el otro es un modelo LTI numérico distinto de un modelo frd, sys es un modelo ss.

    • Si uno de los sistemas conectados es un modelo frd y el otro es un modelo LTI numérico, sys es un modelo frd. Si ambos sistemas son modelos frd, los vectores de frecuencia deben coincidir.

    • Si uno de los sistemas conectados es un modelo LTI identificado, sys también es un modelo identificado.

    • Si uno de los sistemas conectados es un modelo LTI generalizado, como un modelo genss o uss, sys también es un modelo LTI generalizado.

    • Si uno de los sistemas conectados es un modelo disperso, sys es también un modelo disperso.

    Si sys1 y sys2 son arreglos de modelos, sys es un arreglo de modelos del mismo tamaño. Cada entrada de sys es el modelo formado por la conexión de las entradas correspondientes de los arreglos de entrada.

    Historial de versiones

    Introducido antes de R2006a

    Consulte también

    | | |