csaps
Spline cúbico de suavizado
Sintaxis
Descripción
Nota
Encontrará un método para generar splines de suavizado más sencillo pero menos flexible en la app Curve Fitter o en la función fit.
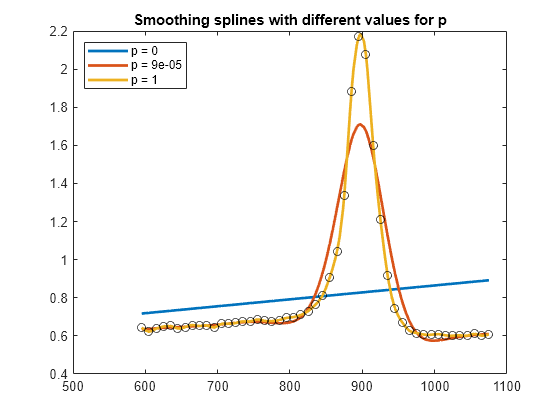
pp = csaps(x,y)(x,y) proporcionados en formato ppform. El valor del spline f en el sitio de datos x(j) aproxima el valor de los datos y(:,j) para j = 1:length(x).
El spline de suavizado f minimiza
Aquí, n es el número de entradas de x y la integral abarca el menor intervalo que contenga todas las entradas de x. yj y xj hacen referencia a las entradas j-ésimas de y y x, respectivamente. D2f indica la segunda derivada de la función f.
Los valores predeterminados de las ponderaciones de medida de errores wj son 1. El valor predeterminado de la función λ de ponderación constante por tramos en la medida de rugosidad es la función constante 1. De forma predeterminada, csaps selecciona un valor para el parámetro de suavizado p a partir de los sitios de datos x proporcionados.
Para evaluar un spline de suavizado fuera de su intervalo básico, antes debe extrapolarlo. Use el comando pp = fnxtr(pp) para garantizar que la segunda derivada sea cero fuera del intervalo que abarcan los sitios de datos.
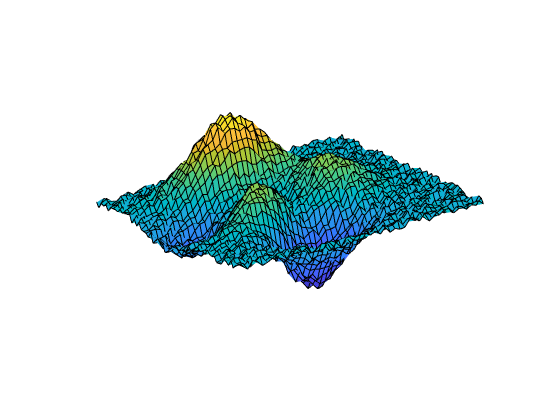
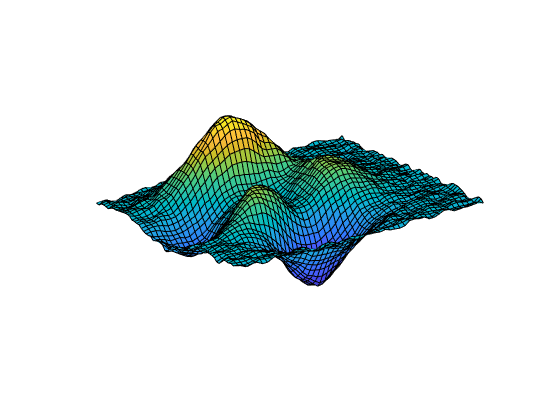
[___] = csaps({x1,...,xm}, proporciona el formato ppform de un spline de suavizado de producto tensorial y,___)m-variado para los datos en la cuadrícula rectangular descrita por {x1,...,xm}. Puede utilizar esta sintaxis con cualquiera de los argumentos de las sintaxis anteriores.
Ejemplos
Argumentos de entrada
Argumentos de salida
Algoritmos
csaps es una implementación de la rutina SMOOTH de Fortran en PGS.
El cálculo del spline de suavizado requiere resolver un sistema lineal cuya matriz de coeficientes tiene la forma p*A + (1-p)*B, donde las matrices A y B dependen de los sitios de datos x. El valor predeterminado de p hace que p*trace(A) sea igual a (1-p)*trace(B).
Historial de versiones
Introducido antes de R2006a