Work with State Transitions
This example shows how to work with transition data from an empirical array of state counts, and create a discrete-time Markov chain (dtmc) model characterizing state transitions. For each quarter in 1857–2022, the example categorizes the state of the US economy as experiencing a recession or expansion by using historical recession periods defined by the National Bureau of Economic Research (NBER). Then, the example forms the empirical transition matrix by counting the quarter-to-quarter transitions of the economic state.
Load and Process Data
Load the historical, NBER-defined recession start and end dates.
load Data_RecessionsThe Recessions variable in the workspace is a 34-by-2 matrix of serial date numbers. Rows of Recessions correspond to successive periods of recession, and columns 1 and 2 contain the start and end dates, respectively. For more details, enter Description at the command line.
Because MATLAB® datetime arrays enable you to work with date data efficiently, convert Recessions to a datetime array. Specify the date format yyyy-MM-dd. Visually compare the data types of the first few periods and the last few periods.
NBERRec = datetime(Recessions,'ConvertFrom',"datenum",... "Format","yyyy-MM-dd"); disptbl = table(Recessions,NBERRec); head(disptbl,3)
Recessions NBERRec
________________________ ______________________
6.7842e+05 6.7897e+05 1857-06-15 1858-12-15
6.7964e+05 6.7988e+05 1860-10-15 1861-06-15
6.8128e+05 6.8226e+05 1865-04-15 1867-12-15
tail(disptbl,3)
Recessions NBERRec
________________________ ______________________
7.3092e+05 7.3117e+05 2001-03-15 2001-11-15
7.3339e+05 7.3394e+05 2007-12-15 2009-06-15
7.3784e+05 7.379e+05 2020-02-15 2020-04-15
Create Array of Visited States
Assume that the sampling period begins on NBERRec(1,1) = 1857-06-15 and ends on 2021-12-10. Create a datetime array of all consecutive quarters in the interval 1857-06-15 through 2021-12-10.
timeline = NBERRec(1,1):calquarters(1):datetime("2021-12-10"); T = numel(timeline); % Sample size
Identify which quarters occur during a recession.
isrecession = @(x)any(isbetween(x,NBERRec(:,1),NBERRec(:,2))); idxrecession = arrayfun(isrecession,timeline);
Create a MATLAB® timetable containing a variable that identifies the economic state of each quarter in the sampling period. Display the first few observations and the last few observations in the timetable.
EconState = repmat("Expansion",T,1); % Preallocation EconState(idxrecession) = "Recession"; Tbl = timetable(EconState,'RowTimes',timeline); head(Tbl,3)
Time EconState
__________ ___________
1857-06-15 "Recession"
1857-09-15 "Recession"
1857-12-15 "Recession"
tail(Tbl,3)
Time EconState
__________ ___________
2021-03-15 "Expansion"
2021-06-15 "Expansion"
2021-09-15 "Expansion"
Tbl is a data set of the observed, quarterly economic states, from which transitions can be counted.
Count State Transitions
Consider creating a 2-by-2 matrix containing the number of:
Transitions from a recession to an expansion
Transitions from an expansion to a recession
Self-transitions of recessions
Self-transitions of expansions
Row and column of the matrix correspond to the same economic state, and element contains the number of transitions from state to state .
First, assign indices to members of the state space.
[idxstate,states] = grp2idx(Tbl.EconState); states
states = 2×1 cell
{'Recession'}
{'Expansion'}
numstates = numel(states);
P = zeros(numstates); % Preallocate transition matrixThe state indices idxstate correspond to states (rows and columns) of the transition matrix, and states defines the indices. P(1,1) is the number of self-transitions of recessions, P(1,2) is the number of transitions from a recession to an expansion, and so on. Therefore, to count the transition types in the data efficiently, for every transition to , tally the observed transition by indexing into the transition matrix using state indices at times (row) and (column).
for t = 1:(T - 1) P(idxstate(t),idxstate(t+1)) = P(idxstate(t),idxstate(t+1)) + 1; end array2table(P,'VariableNames',states,'RowNames',states)
ans=2×2 table
Recession Expansion
_________ _________
Recession 171 34
Expansion 33 419
P is the matrix of observed transitions. P(1,2) = 34 means that the US economy transitioned from a recession to an expansion 34 times between 1857-06-15 and 2021-12-10.
Create Discrete-Time Markov Chain
Create a discrete-time Markov chain model characterized by the transition matrix P.
mc = dtmc(P,'StateNames',states); array2table(mc.P,'VariableNames',states,'RowNames',states)
ans=2×2 table
Recession Expansion
_________ _________
Recession 0.83415 0.16585
Expansion 0.073009 0.92699
mc is a dtmc object. dtmc normalizes P to create the right-stochastic transition matrix mc.P (each row sums to 1). The element mc.P(1,2) = 0.1659 means that the empirical probability of transitioning to an expansion at time + 1, given that the US economy is in a recession at time , is 0.1659.
Plot a directed graph of the Markov chain.
graphplot(mc,'LabelEdges',true)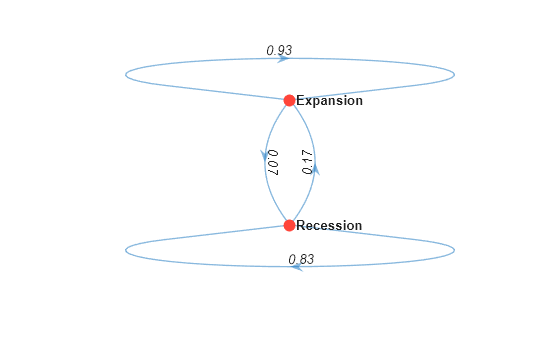
The Markov chain suggests that the current economic state tends to persist, from quarter to quarter.