Estimar un modelo de proceso
Realizar la estimación de un modelo de proceso en tiempo continuo para un sistema de única entrada y única salida (SISO) en el dominio del tiempo o la frecuencia en Live Editor
Descripción
La tarea Estimate Process Model permite estimar y validar de manera interactiva un modelo de proceso para sistemas SISO. Puede definir y variar la estructura del modelo y especificar parámetros opcionales, como el método de gestión de la condición inicial y de búsqueda. La tarea genera automáticamente código de MATLAB® para un script en vivo. Para obtener más información sobre las tareas de Live Editor en general, consulte Add Interactive Tasks to a Live Script.
Los modelos de proceso son funciones de transferencia en tiempo continuo sencillas que describen la dinámica del sistema lineal. Los elementos de un modelo de proceso incluyen ganancia estática, constantes de tiempo, retardos de tiempo, integrador y cero de proceso.
Los modelos de proceso son populares para describir dinámicas de sistema en muchos sectores y son aplicables a distintos entornos de producción. Las ventajas de estos modelos son que son sencillos, admiten estimación del retardo de transporte y los coeficientes del modelo son fáciles de interpretar como polos y ceros. Para obtener más información sobre la estimación de modelos de procesos, consulte What Is a Process Model?
La tarea Estimate Process Model es independiente de la app más general System Identification. Utilice la app System Identification cuando desee calcular y comparar estimaciones para varias estructuras de modelo.
Para comenzar, cargue datos de experimentos que contengan datos de entrada y salida en el área de trabajo de MATLAB y, después, importe esos datos a la tarea. Después, seleccione una estructura de modelo que se va a estimar. La tarea proporciona controles y gráficas que permiten experimentar con diferentes estructuras de modelo y comparar cuán bien se ajusta la salida de cada modelo a las mediciones.
Abrir la tarea
Para añadir la tarea Estimate Process Model a un script en vivo en el editor de MATLAB:
En la pestaña Live Editor, seleccione Task > Estimate Process Model.
En un bloque de código de su script, escriba una palabra clave relevante, como
processoestimate. SeleccioneEstimate Process Modelde entre las terminaciones de comandos sugeridas.
Ejemplos
Utilice la tarea Estimate Process Model de Live Editor para estimar un modelo de proceso y comparar la salida del modelo con los datos de medición.
Configurar datos
Cargue los datos de medición tt1 en el área de trabajo de MATLAB. tt1 es un horario que contiene una variable de entrada u y una variable de salida y.
load sdata1 tt1
Importar datos a la tarea
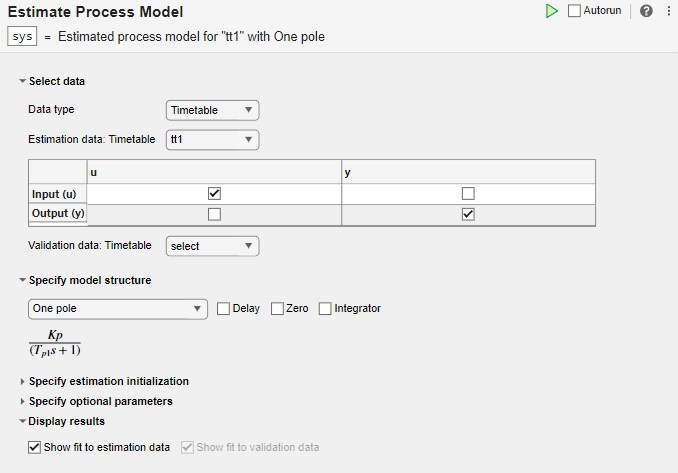
En la sección Select data, establezca Data type en Timetable y establezca Estimation data en tt1.
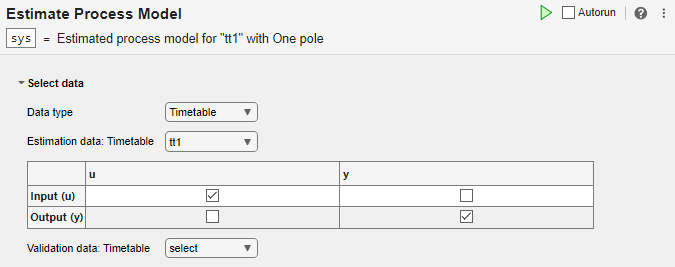
La tarea muestra una tabla que contiene los nombres de la variable de entrada y de salida de tt1.
Realizar la estimación del modelo utilizando la configuración predeterminada
Examine la estructura del modelo y los parámetros opcionales.
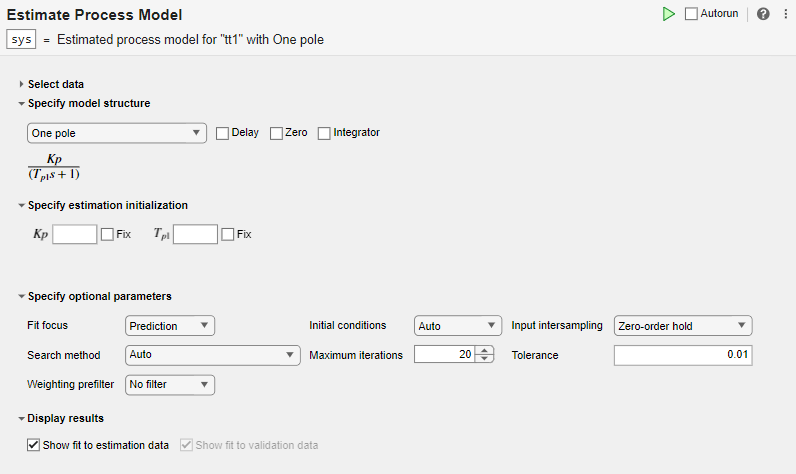
En la sección Specify model structure , la opción predeterminada es One Pole sin retardo, cero o integrador. Las ecuaciones debajo de los parámetros de esta sección muestran la estructura especificada.
En la sección Specify estimation initialization, los parámetros de inicialización que coinciden con los parámetros de la estructura del modelo permiten establecer puntos de partida para la estimación. Si selecciona Fix, el parámetro permanece fijo en el valor que especifique. Para este ejemplo, no especifique la inicialización. La tarea utiliza entonces valores predeterminados para los puntos de partida.
En la sección Specify optional parameters, las opciones predeterminadas para la estimación del proceso están establecidas.
Ejecute la tarea desde la pestaña Live Editor haciendo clic en la flecha verde. También puede seleccionar Autorun para ejecutar la tarea automáticamente cada vez que actualice un parámetro.
![]()
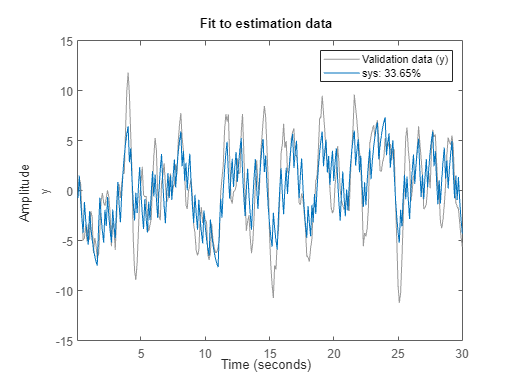
Una gráfica muestra los datos de estimación, la salida del modelo estimado y el porcentaje de ajuste.
Experimentar con la configuración de parámetros
Experimente con la configuración de parámetros y descubra cómo influyen en el ajuste.
Por ejemplo, añada retardo a la estructura One Pole y ejecute la tarea.
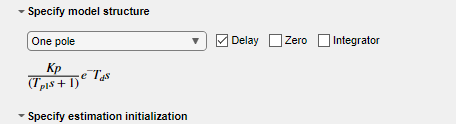
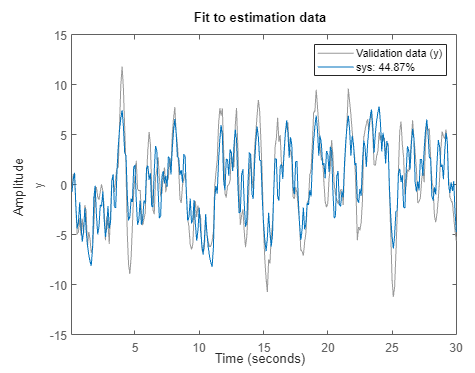
El ajuste de la estimación mejora, aunque el porcentaje de ajuste sigue estando por debajo del 50%.
Pruebe una estructura de modelo diferente. En Specify model structure, seleccione Underdamped Pair sin retardo y ejecute la tarea.
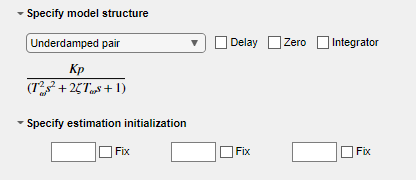
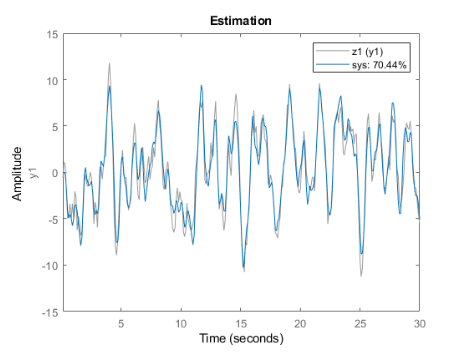
Los resultados del ajuste mejoran de manera significativa.
Generar código
Para mostrar el código que la tarea genera, haga clic en ![]() , en la parte inferior de la sección de parámetros. El código que se muestra refleja la configuración de parámetros actual de la tarea.
, en la parte inferior de la sección de parámetros. El código que se muestra refleja la configuración de parámetros actual de la tarea.
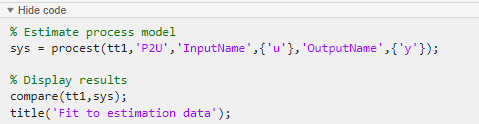
Utilice datos de estimación y de validación independientes para poder validar el modelo de proceso estimado.
Configurar datos
Cargue los datos de medición sdata1 en el área de trabajo de MATLAB y examine el contenido.
load sdata1 umat1 ymat1 Ts
Divida los datos en dos conjuntos, la mitad para la estimación y la mitad para la validación. El conjunto de datos original tiene 300 muestras, de modo que cada conjunto de datos nuevo tiene 150 muestras.
u_est = umat1(1:150); u_val = umat1(151:300); y_est = ymat1(1:150); y_val = ymat1(151:300); Ts
Ts = 0.1000
Importar datos a la tarea
En la sección Select data, establezca Data type en Numeric. Establezca el tiempo de muestreo en 0.1 segundos. Seleccione los conjuntos de datos adecuados para la estimación y la validación.
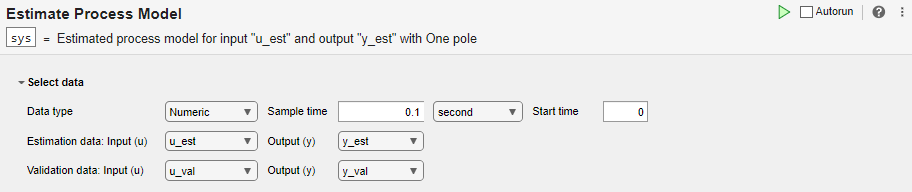
Realizar la estimación y validación del modelo
El ejemplo Realizar la estimación de un modelo de proceso con una tarea de Live Editor consigue los mejores resultados utilizando la estructura de modelo Underdamped Pair. Elija la misma opción para este ejemplo.
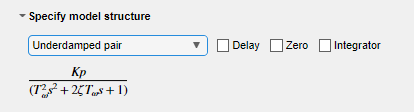
Ejecute la tarea. Cuando se ejecuta la tarea, se crean dos gráficas. La primera gráfica muestra los resultados de la estimación y la segunda gráfica, los resultados de la validación.
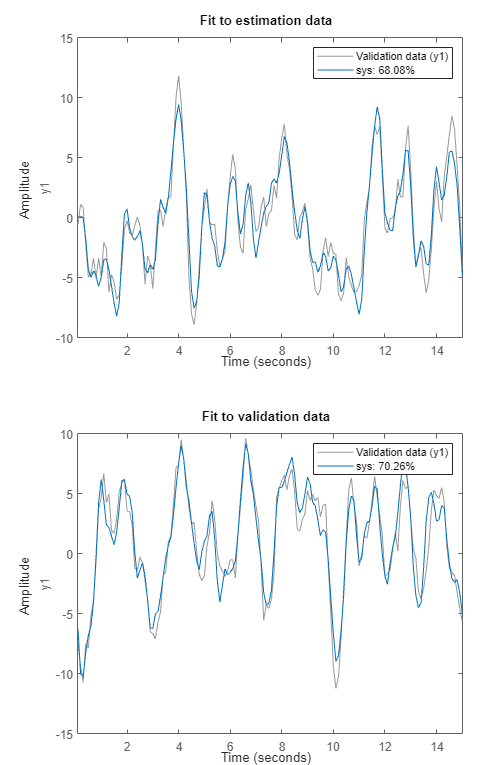
El ajuste a los datos de estimación es inferior al obtenido en Realizar la estimación de un modelo de proceso con una tarea de Live Editor. La estimación en el ejemplo actual solo tiene la mitad de los datos con los que estimar el modelo. El ajuste a los datos de validación, que representa la bondad del modelo de forma más general, es superior al ajuste a los datos de estimación.
Parámetros
Seleccionar datos
La tarea acepta valores de medición numéricos que están muestreados de manera uniforme en el tiempo. Las señales de entrada y salida pueden contener múltiples canales. Los datos se pueden empaquetar como arreglos numéricos (para Numeric o Frequency), como un horario o en un objeto de datos, como un objeto iddata o idfrd. Para datos multiexperimento, los datos numéricos y de horario pueden empaquetarse como arreglos de celdas. Para arreglos de celdas de horarios, todos los horarios deben contener los mismos nombres de variable. Los objetos de datos gestionan los datos multiexperimento internamente.
El tipo de datos que se elige determina si se deben o no especificar parámetros adicionales.
Numeric: especifique Sample Time y Start Time en las unidades de tiempo que seleccione.Timetable: no especifique parámetros adicionales porque el horario ya contiene información sobre el tiempo de muestreo y el tiempo de inicio.Frequency: especifique Frequency seleccionando el nombre de variable de un vector de frecuencia en el área de trabajo de MATLAB. Especifique las unidades para este vector de frecuencia. Especifique Sample Time en segundos.Data Object: no especifique parámetros adicionales porque el objeto de datos ya contiene información sobre el muestreo de tiempo o frecuencia.
Seleccione los nombres de variable de entrada y salida de las opciones del área de trabajo de MATLAB. Utilice estos parámetros cuando Data Type es Numeric o Frequency.
Especificar datos de validación es opcional pero recomendable.
Seleccione el nombre de variable del horario de las opciones del área de trabajo de MATLAB. Utilice este parámetro cuando Data Type es Timetable. La tarea muestra los nombres de la variable del horario para la entrada y salida. Los horarios de estimación y validación deben contener los mismos nombres de variable.
Seleccione el nombre de variable del objeto de datos de las opciones del área de trabajo de MATLAB. Utilice este parámetro cuando Data Type es Data Object.
Especificar una estructura de modelo
La tarea permite especificar una de cuatro estructuras básicas. Estas estructuras van desde un proceso de primer orden sencillo hasta un proceso de segundo orden o tercer orden más dinámico con polos complejos conjugados (subamortiguados).
One PoleTwo Real PolesUnderdamped PairUnderdamped Pair + Real Pole
Incluya retardo de transporte o retardo de entrada a salida de una muestra. El retardo de transporte también se conoce como retardo puro.
Incluya un cero de proceso en el numerador.
Incluya un integrador, representado por un término adicional 1/ s. Si se incluye un integrador, se crea un proceso autorregulador.
Especificar inicialización de una estimación
Especifique los valores iniciales para la estimación y si estos valores deben ser fijos o deben estimarse. Los valores que se desean especificar dependen de la estructura de modelo y de las especificaciones para Delay y Zero. En Specify model structure, la tarea muestra la ecuación que representa el sistema especificado. Esta ecuación contiene todos los parámetros que se pueden estimar y que se pueden inicializar o fijar. Los parámetros posibles son:
Kp: ganancia estática
Tp1: constante de tiempo para el primer polo real
Tp2: constante de tiempo para el segundo polo real
Tω: constante de tiempo para polos complejos, igual a la inversa de la frecuencia natural
ζ: coeficiente de amortiguación para polos complejos
Td: retardo de transporte
Tz: constante de tiempo para el cero de proceso
Todos los parámetros basados en el tiempo se expresan en las unidades de tiempo seleccionadas para Sample Time.
Especificar parámetros opcionales
Fit Focus especifica qué error minimizar en la función de pérdida durante la estimación.
Prediction: minimiza el error de predicción a un paso por adelantado entre la salida medida y la prevista. Este enfoque de estimación se centra en generar un buen modelo de predicción para las entradas y salidas de estimación. El enfoque de predicción genera normalmente los mejores resultados de estimación porque utiliza tanto las mediciones de entrada como de salida, teniendo en cuenta, por lo tanto, las perturbaciones.Simulation: minimiza el error entre la salida medida y la de simulación. Este enfoque de estimación se centra en generar una respuesta del modelo simulada que se ajusta bien a las entradas y salidas de estimación. El enfoque de simulación es, por lo general, mejor para la validación, especialmente con conjuntos de datos no usados para la estimación original.
Establezca esta opción cuando desee elegir un método específico para inicializar el modelo. Con la configuración predeterminada de Auto, el software elige el método en función de los datos de estimación. Las opciones son:
Zero: el estado inicial se establece en cero.Estimate: el estado inicial se trata como un parámetro de estimación independiente.Backcast: el estado inicial se estima utilizando el mejor ajuste con mínimos cuadrados.
El intermuestreo de entrada es una propiedad de los datos de entrada. La tarea utiliza esta propiedad cuando estima modelos de proceso. Especifique Input Intersampling cuando el tipo de datos es Time o Frequency. Si está utilizando un objeto iddata, el objeto ya contiene la información de intermuestreo. Las opciones para esta propiedad son:
Zero-order hold: señal de entrada constante por partes entre muestrasTriangle approximation: señal de entrada lineal por partes entre muestras, también conocida como retención de primer ordenBand-limited: la señal de entrada no tiene potencia por encima de la frecuencia Nyquist
Los métodos de búsqueda numéricos disponibles para la estimación iterativa de parámetros son:
| Método de búsqueda | Descripción |
|---|---|
Auto | Para cada iteración, el software vuelve a utilizar los métodos hasta que encuentra la primera dirección descendente que genera una reducción del coste de estimación. |
Gauss-Newton | Los valores singulares de la matriz jacobiana inferiores a GnPinvConstant*eps*max(size(J))*norm(J) se descartan cuando se calcula la dirección de búsqueda. J es la matriz jacobiana. La matriz hessiana se aproxima como JTJ. Si esta dirección no muestra una mejora, la función prueba la dirección del gradiente. |
Adaptive Gauss-Newton | Los valores propios inferiores a gamma*max(sv) de la matriz hessiana se ignoran, donde sv contiene los valores singulares de la matriz hessiana. La dirección de Gauss-Newton se calcula en el subespacio restante. gamma tiene el valor inicial InitialGnaTolerance (consulte Advanced en 'SearchOptions' para obtener más información). Este valor se incrementa por el factor LMStep cada vez que la búsqueda no encuentra un valor inferior del criterio en menos de cinco bisecciones. Este valor se reduce por el factor 2*LMStep cada vez que una búsqueda se realiza con éxito sin bisecciones. |
Levenberg-Marquardt | Cada valor de parámetro es -pinv(H+d*I)*grad respecto del valor anterior. H es la matriz hessiana, I es la matriz de identidad y grad es el gradiente. d es un número que se incrementa hasta que se encuentra un valor inferior del criterio. Este método requiere Optimization Toolbox™. Para obtener más información, consulte Método de Levenberg-Marquardt (Optimization Toolbox). |
Gradient search | Búsqueda de mínimos cuadrados con descenso más pronunciado. |
Trust-Region Reflective Newton | Un solver no lineal restringido. Este solver requiere Optimization Toolbox. Para obtener más información, consulte Algoritmo fmincon trust-region-reflective (Optimization Toolbox). |
Pattern Search | Solver para no linealidades sin gradientes bien definidos. Este solver requiere Global Optimization Toolbox. Para obtener más información, consulte patternsearch (Global Optimization Toolbox). |
Sequential Quadratic Programming (SQP) | Un solver no lineal restringido. Este solver requiere Optimization Toolbox. Para obtener más información, consulte Algoritmo SQP de fmincon (Optimization Toolbox). |
Interior-Point | Un solver no lineal restringido. Este solver requiere Optimization Toolbox. Para obtener más información, consulte Algoritmo interior-point de fmincon (Optimization Toolbox). |
Establezca el número máximo de iteraciones durante la minimización de errores. Las iteraciones se detienen cuando se alcanza Max. Iterations o se cumple otro criterio de detención, como Tolerance.
Cuando el porcentaje de la mejora esperada es inferior a Tolerance, las iteraciones se detienen.
Establezca esta opción cuando desee aplicar un prefiltro de peso a la función de pérdida que la tarea minimiza cuando se estima el modelo. Cuando selecciona una opción, también debe seleccionar en el área de trabajo la variable asociada que contiene la información del filtro. Las opciones disponibles dependen del dominio de los datos.
| Prefiltro de peso | Dominio de los datos | Información del filtro |
|---|---|---|
No Filter | Tiempo y frecuencia | |
Passbands | Tiempo y frecuencia | Rangos de banda de paso, especificados como vector fila de 1 por 2 o matriz de n por 2, donde n es el número de bandas de paso |
LTI Filter | Tiempo y frecuencia | Modelo LTI SISO |
Frequency Weights Vector | Frecuencia | Pesos de frecuencia, especificados como vector columna con la misma longitud que el vector de frecuencia |
Por ejemplo, supongamos que está realizando una estimación con datos SISO del dominio de la frecuencia y que en el área de trabajo de MATLAB tiene un vector columna W que contiene pesos de frecuencia para el prefiltro. En la tarea, seleccione Weighting prefilter > Frequency weights vector y la variable W.
Visualizar resultados
Represente una comparación de la salida del modelo y de los datos originales medidos, junto con el porcentaje de ajuste. Si tiene datos de validación independientes, una segunda gráfica compara la respuesta del modelo a los datos de entrada de validación con la salida medida del conjunto de datos de validación.
Historial de versiones
Introducido en R2019bAhora puede estimar un sistema que tiene una no linealidad sin un gradiente bien definido eligiendo Search Method como Pattern Search. Este método requiere Global Optimization Toolbox.
La tarea Estimate Process Model de Live Editor admite ahora datos multiexperimento.
Se ha actualizado la tarea para aceptar datos del dominio del tiempo con el formato de un horario. La tarea sigue aceptando también datos del dominio del tiempo numéricos, con la opción de tipo de datos Numeric.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)