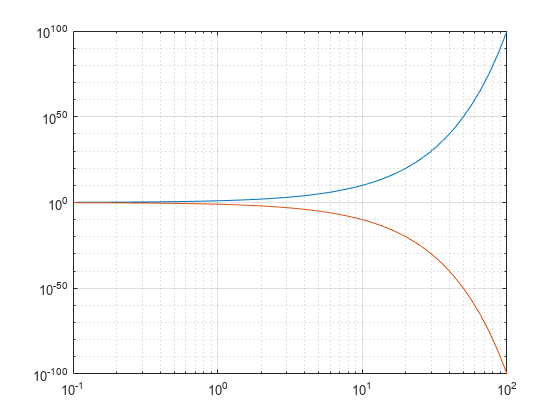
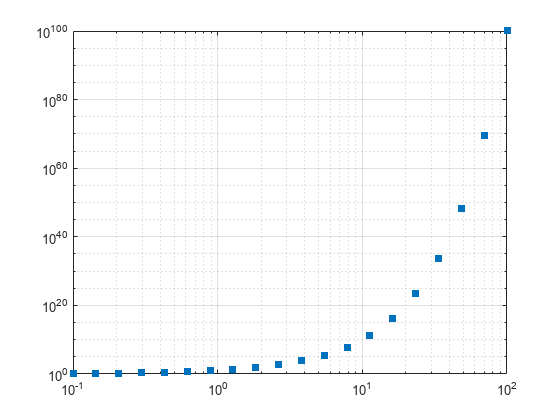
loglog
Gráfica de escala logarítmica
Sintaxis
Descripción
Datos de vectores y matrices
loglog( representa las coordenadas x e y utilizando una escala logarítmica de base 10 en el eje x y en el eje y.X,Y)
Para representar un grupo de coordenadas conectadas por segmentos de línea, especifique
XeYcomo vectores de la misma longitud.Para representar múltiples grupos de coordenadas en el mismo conjunto de ejes, especifique al menos
XoYcomo matriz.
loglog( representa Y)Y con respecto a un grupo implícito de coordenadas x.
Si
Yes un vector, las coordenadas x oscilan entre 1 ylength(Y).Si
Yes una matriz, la gráfica contiene una línea para cada columna deY. Las coordenadas x oscilan de 1 al número de filas deY.
Si Y contiene números complejos, loglog representa la parte imaginaria de Y frente a la parte real de Y. Sin embargo, si especifica tanto X como Y, MATLAB® ignora la parte imaginaria.
Datos de tabla
loglog( representa las variables tbl,xvar,yvar)xvar y yvar desde la tabla tbl. Para representar un conjunto de datos, especifique una variable para xvar y una variable para yvar. Para representar varios conjuntos de datos, especifique múltiples variables para xvar, yvar o ambas. Si ambos argumentos especifican múltiples variables, deben especificar el mismo número de variables. (desde la versión R2022a)
Otras opciones
loglog( muestra la gráfica en los ejes objetivo. Especifique los ejes como el primer argumento en cualquiera de las sintaxis anteriores.ax,___)
loglog(___, especifica las propiedades de Name,Value)Line utilizando uno o más argumentos nombre-valor. Las propiedades se aplican a todas las líneas representadas. Especifique los argumentos nombre-valor después de todos los argumentos de cualquiera de las sintaxis anteriores. Para obtener una lista de las propiedades, consulte Line Properties.
p = loglog(___) devuelve un objeto de Line o un arreglo de objetos de Line. Use p para modificar las propiedades de la gráfica después de crearla. Para obtener una lista de las propiedades, consulte Line Properties.
Ejemplos
Argumentos de entrada
Argumentos de par nombre-valor
Sugerencias
Utilice
NaNoInfpara crear saltos en las líneas. Por ejemplo, este código representa una línea con un salto entrey=2ey=4.loglog([1 2 3 4 5],[1 2 NaN 4 5])
La función
loglogutiliza los colores y los estilos de línea basados en las propiedadesColorOrderyLineStyleOrderde los ejes.loglogajusta los colores en el primer estilo de línea. Luego, vuelve a ajustar los colores en cada estilo de línea adicional.Puede cambiar los colores y los estilos de línea después de representarlos estableciendo las propiedades
ColorOrderoLineStyleOrderen los ejes. También puede llamar a la funcióncolororderpara cambiar el orden de los colores en todos los ejes de la figura.
Algoritmos
La función loglog representa coordenadas en una escala logarítmica estableciendo las propiedades XScale e YScale de los ejes en 'log'. Sin embargo, si el estado hold de los ejes es 'on' antes de llamar a loglog, esas propiedades no cambian, y la gráfica podría mostrarse en una escala lineal o semilogarítmica.