pchip
Polinomio de interpolación cúbica de Hermite por tramos (PCHIP)
Sintaxis
Descripción
p = pchip(x,y,xq)p que corresponden a los puntos de consulta en xq. Los valores de p están determinados por la interpolación cúbica por tramos que conserva la forma de x e y.
Ejemplos
Argumentos de entrada
Argumentos de salida
Más acerca de
Sugerencias
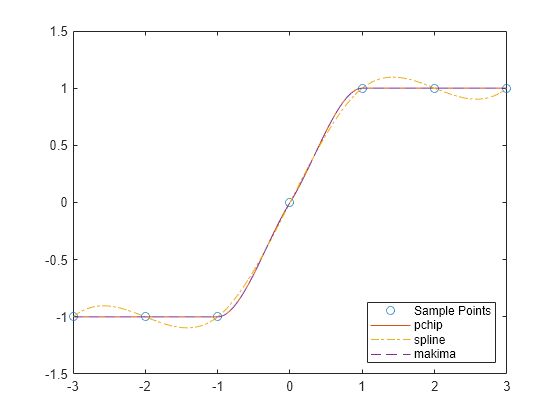
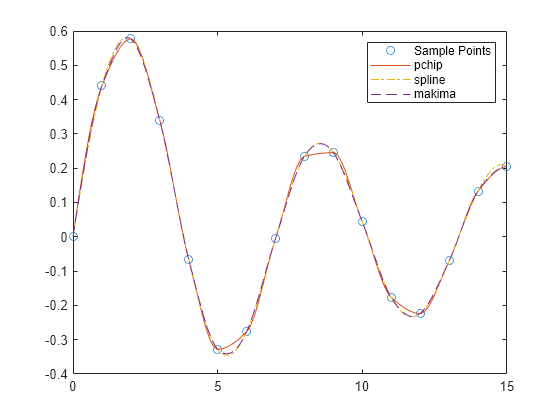
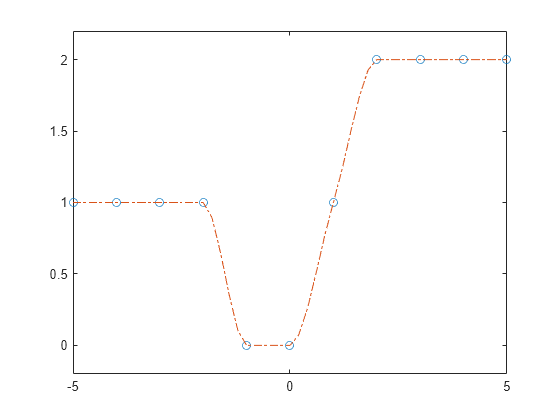
splineconstruye de casi la misma forma quepchipconstruye . Sin embargo,splineelige las pendientes en de forma diferente, a saber, para hacer que sea incluso continua. Esta diferencia tiene varios efectos:splineproduce un resultado más suave, de modo que sea continua.splineproduce un resultado más preciso si los datos constan de valores de una función suavizada.pchipno tiene sobreimpulsos y tiene menos oscilación si los datos no son suaves.pchipes menos costosa de configurar.Ambas son igual de costosas de evaluar.
Referencias
[1] Fritsch, F. N. and R. E. Carlson. "Monotone Piecewise Cubic Interpolation." SIAM Journal on Numerical Analysis. Vol. 17, 1980, pp.238–246.
[2] Kahaner, David, Cleve Moler, Stephen Nash. Numerical Methods and Software. Upper Saddle River, NJ: Prentice Hall, 1988.
Capacidades ampliadas
Historial de versiones
Introducido antes de R2006a