spline

Interpolación de datos por splines cúbicos

Sintaxis

s = spline(x,y,xq)

pp = spline(x,y)

Descripción

s = spline(x,y,xq) devuelve un vector de valores interpolados s que corresponden a los puntos de consulta en xq. Los valores de s están determinados por la interpolación por splines cúbicos de x e y.

pp = spline(x,y) devuelve una estructura polinómica por tramos para su uso por ppval y la utilidad de spline unmkpp.

Ejemplos

Interpolación por splines de datos de seno

Utilice spline para interpolar una curva de seno sobre puntos de muestra espaciados de forma irregular.

x = [0 1 2.5 3.6 5 7 8.1 10];
y = sin(x);
xx = 0:.25:10;
yy = spline(x,y,xx);
plot(x,y,'o',xx,yy)

Interpolación por splines con pendientes de punto final especificadas

Utilice la interpolación por splines restringida o completa cuando conozca las pendientes de punto final. Para ello, puede especificar el vector de valores $\mathit{y}$ con dos elementos adicionales, uno al principio y otro al final, para definir las pendientes de punto final.

Cree un vector de datos $\mathit{y}$ y otro vector con las coordenadas $\mathit{x}$ de los datos.

x = -4:4;
y = [0 .15 1.12 2.36 2.36 1.46 .49 .06 0];

Interpole los datos utilizando spline y represente los resultados. Especifique la segunda entrada con dos valores adicionales [0 y 0] para significar que ambas pendientes de punto final son cero. Utilice ppval para evaluar el ajuste por splines sobre 101 puntos en el intervalo de interpolación.

cs = spline(x,[0 y 0]);
xx = linspace(-4,4,101);
plot(x,y,'o',xx,ppval(cs,xx),'-');

Extrapolación con spline cúbico

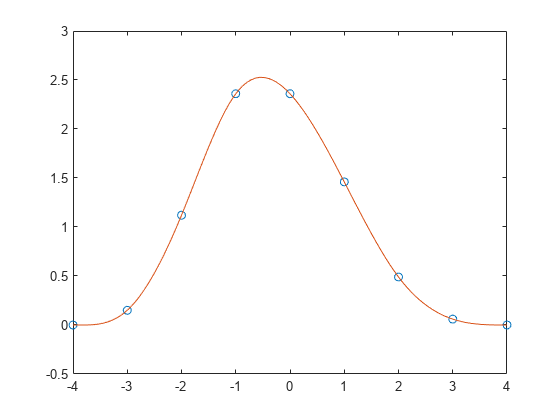
Extrapole un conjunto de datos para predecir el crecimiento de la población.

Cree dos vectores para representar los años del censo, desde 1900 hasta 1990 (t), y la población estadounidense correspondiente en millones de personas (p).

t = 1900:10:1990;
p = [ 75.995  91.972  105.711  123.203  131.669 ...
     150.697 179.323  203.212  226.505  249.633 ];

Extrapole y prediga la población en el año 2000 utilizando un spline cúbico.

spline(t,p,2000)

ans = 
270.6060

Interpolación por splines de datos angulares

Genere la representación de un círculo con los cinco puntos de datos y(:,2),...,y(:,6) marcados con una "o". La matriz y contiene dos columnas más que la x. Por lo tanto, spline utiliza y(:,1) e y(:,end) como pendientes finales. El círculo empieza y acaba en el punto (1,0), de modo que el punto se representa dos veces.

x = pi*[0:.5:2]; 
y = [0  1  0 -1  0  1  0; 
     1  0  1  0 -1  0  1];
pp = spline(x,y);
yy = ppval(pp, linspace(0,2*pi,101));
plot(yy(1,:),yy(2,:),'-b',y(1,2:5),y(2,2:5),'or')
axis equal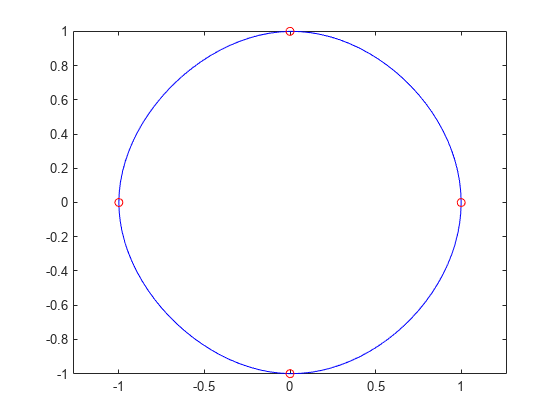

Interpolación por splines de datos de seno y coseno

Utilice el spline para muestrear una función sobre una malla más precisa.

Genere curvas de seno y de coseno para unos pocos valores entre 0 y 1. Utilice la interpolación por splines para muestrear una función sobre una malla más precisa.

x = 0:.25:1;
Y = [sin(x); cos(x)];
xx = 0:.1:1;
YY = spline(x,Y,xx);
plot(x,Y(1,:),'o',xx,YY(1,:),'-')
hold on
plot(x,Y(2,:),'o',xx,YY(2,:),':')
hold off

Interpolación de datos con spline, pchip y makima

Compare los resultados de la interpolación que han producido spline, pchip y makima para dos conjuntos de datos diferentes. Todas estas funciones realizan formas diferentes de interpolación cúbica de Hermite por tramos. Cada función difiere del resto en el modo en que calcula las pendientes de la interpolación, lo que resulta en diferentes comportamientos cuando los datos subyacentes contienen zonas planas u ondulaciones.

Compare los resultados de la interpolación en los datos de la muestra que conectan las zonas planas. Cree vectores de valores x, valores de función en esos puntos y, y puntos de consulta xq. Calcule las interpolaciones en los puntos de consulta utilizando spline, pchip y makima. Represente los valores de la función interpolada en los puntos de consulta para compararlos.

x = -3:3; 
y = [-1 -1 -1 0 1 1 1]; 
xq1 = -3:.01:3;
p = pchip(x,y,xq1);
s = spline(x,y,xq1);
m = makima(x,y,xq1);
plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--')
legend('Sample Points','pchip','spline','makima','Location','SouthEast')

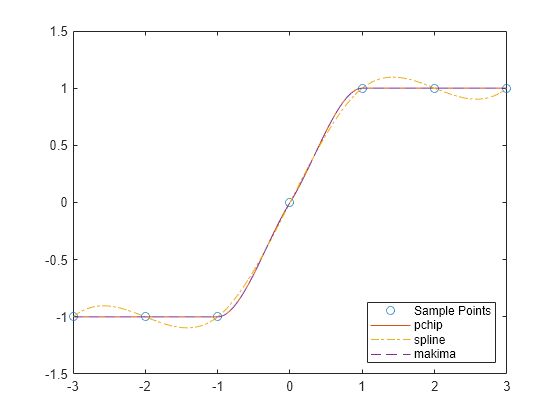
En este caso, pchip y makima presentan un comportamiento similar porque evitan los sobreimpulsos y pueden conectar las zonas planas con precisión.

Realice una segunda comparación utilizando una función de muestra oscilatoria.

x = 0:15;
y = besselj(1,x);
xq2 = 0:0.01:15;
p = pchip(x,y,xq2);
s = spline(x,y,xq2);
m = makima(x,y,xq2);
plot(x,y,'o',xq2,p,'-',xq2,s,'-.',xq2,m,'--')
legend('Sample Points','pchip','spline','makima')

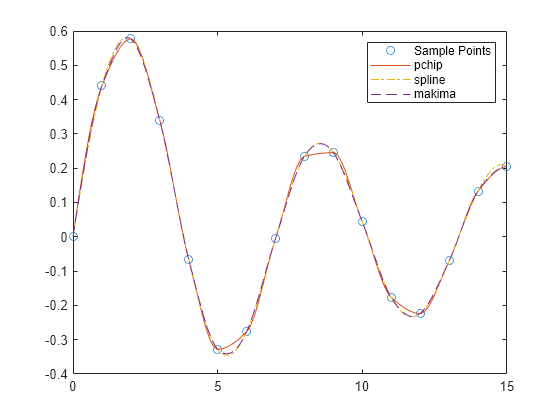
Cuando la función subyacente es oscilatoria, spline y makima capturan el movimiento entre puntos mejor que pchip, que se aplana de forma pronunciada cerca de los extremos locales.

Argumentos de entrada

x — Coordenadas x

vector

Coordenadas x, especificadas como un vector. El vector x especifica los puntos en los que se dan los datos y. Los elementos de x deben ser únicos.

La interpolación por splines cúbicos requiere al menos 4 puntos, y se recurre a la interpolación lineal o cuadrática si se proporcionan 2 o 3 puntos, respectivamente.

Tipos de datos: single | double

y — Valores de función en las coordenadas x

vector | matriz | arreglo

Valores de función en las coordenadas x, especificados como un vector, matriz o arreglo numérico. x e y suelen tener la misma longitud, pero y también puede tener exactamente dos elementos más que x para especificar las pendientes finales.

Cuando y es una matriz o un arreglo, los valores de la última dimensión, y(:,...,:,j), se toman como valores que coinciden con x. En este caso, la última dimensión de y debe tener la misma longitud que x o tener exactamente dos elementos más.

Las pendientes finales del spline cúbico siguen estas reglas:

• Cuando x e y son vectores del mismo tamaño, se aplican las condiciones finales de "no es un nudo".

• Cuando x o y son un escalar, se expanden para tener la misma longitud que la otra y se aplican las condiciones finales de "no es un nudo".

• Cuando y es un vector que contiene dos o más valores que entradas tiene x, spline utiliza el primer y el último valor de y como pendientes finales del spline cúbico. Por ejemplo, cuando y es un vector:

  • y(2:end-1) proporciona los valores de la función en cada punto de x.

  • y(1) proporciona la pendiente al principio del intervalo situado en min(x).

  • y(end) proporciona la pendiente al final del intervalo situado en max(x).

• Del mismo modo, cuando y es una matriz o un arreglo de N dimensiones donde size(y,N) es igual a length(x)+2:

  • y(:,...,:,j+1) proporciona los valores de la función en cada punto de x para j = 1:length(x).

  • y(:,:,...:,1) proporciona las pendientes al principio de los intervalos situados en min(x).

  • y(:,:,...:,end) proporciona las pendientes al final de los intervalos situados en max(x).

Tipos de datos: single | double

xq — Puntos de consulta

escalar | vector | matriz | arreglo

Puntos de consulta, especificados como escalar, vector, matriz o arreglo. Los puntos especificados en xq son las coordenadas x de los valores de la función interpolada yq calculados por spline.

Tipos de datos: single | double

Argumentos de salida

s — Valores interpolados en puntos de consulta

escalar | vector | matriz | arreglo

Valores interpolados en puntos de consulta, devueltos como escalar, vector, matriz o arreglo.

El tamaño de s está relacionado con los tamaños de y y xq:

• Cuando y es un vector, s tiene el mismo tamaño que xq.

• Cuando y es un arreglo de tamaño Ny = size(y), se aplican las condiciones siguientes:

  • Cuando xq es un escalar o un vector, size(s) devuelve [Ny(1:end-1) length(xq)].

  • Cuando xq es un arreglo, size(s) devuelve [Ny(1:end-1) size(xq)].

pp — Polinomio por tramos

estructura

Polinomio por tramos, devuelto como una estructura. Utilice esta estructura con la función ppval para evaluar el polinomio por tramos en uno o más puntos de consulta. Esta estructura contiene estos campos.

Campo	Descripción
form	'pp' para polinomio por tramos
breaks	Vector de longitud L+1 con elementos estrictamente crecientes que representan el inicio y el final de cada uno de los intervalos L
coefs	Matriz de L por k con cada fila coefs(i,:) que contiene los coeficientes locales de un polinomio de orden k en el i-ésimo intervalo, [breaks(i),breaks(i+1)]
pieces	Número de tramos, L
order	Orden de los polinomios
dim	Dimensionalidad del destino

Dado que los coeficientes del polinomio de coefs son coeficientes locales para cada intervalo, deberá restar el punto final más bajo del intervalo de nudos correspondiente para utilizar los coeficientes en una ecuación polinómica convencional. En otras palabras, para los coeficientes [a,b,c,d] del intervalo [x1,x2], el polinomio correspondiente es

$$f\left(x\right)=a{\left(x-x_1\right)}^3+b{\left(x-x_1\right)}^2+c\left(x-x_1\right)+d.$$

Sugerencias

• También puede realizar la interpolación por splines utilizando la función interp1 con el comando interp1(x,y,xq,'spline'). Mientras que spline realiza la interpolación en las filas de una matriz de entrada, interp1 lo hace en las columnas de la matriz de entrada.

Algoritmos

Un sistema lineal tridiagonal (posiblemente con varios laterales derechos) se resuelve para obtener la información necesaria para describir los coeficientes de los diversos polinomios cúbicos que conforman el spline de interpolación. spline utiliza las funciones ppval, mkpp y unmkpp. Estas rutinas forman un pequeño conjunto de funciones para trabajar con polinomios por tramos. Para acceder a funcionalidades más avanzadas, consulte interp1 o las funcionalidades de splines de Curve Fitting Toolbox™.

Referencias

[1] de Boor, Carl. A Practical Guide to Splines. Springer-Verlag, New York: 1978.

Capacidades ampliadas

Generación de código C/C++

Genere código C y C++ mediante MATLAB® Coder™.

Notas y limitaciones de uso:

• La entrada x debe ser estrictamente creciente.

• La generación de código no elimina las entradas y con valores NaN.

• La generación de código no informa de un error con pendientes finales infinitas en y.

• Si genera código para la sintaxis pp = spline(x,y), no podrá introducir pp en la función ppval de MATLAB^®. Para crear una estructura pp de MATLAB a partir de una estructura pp creada por el generador de código:

  • Al generar código, utilice unmkpp para devolver los detalles del polinomio por tramos a MATLAB.

  • En MATLAB, utilice mkpp para crear la estructura pp.

• Si proporciona xq y y presenta un tamaño variable y no es un vector de longitud variable, la orientación de las salidas de los vectores del código generado podría no coincidir con la orientación en MATLAB.

Entorno basado en subprocesos

Ejecute código en segundo plano con MATLAB® backgroundPool o acelere código con Parallel Computing Toolbox™ ThreadPool.

Esta función es totalmente compatible con entornos basados en subprocesos. Para obtener más información, consulte Ejecutar funciones de MATLAB en entornos basados en subprocesos.

Arreglos GPU

Acelere código mediante la ejecución en una unidad de procesamiento gráfico (GPU) mediante Parallel Computing Toolbox™.

La función spline es compatible con entradas de arreglos de GPU con estas notas y limitaciones de uso:

• El argumento de entrada y no puede ser disperso.

Para obtener más información, consulte Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Historial de versiones

Introducido antes de R2006a

Consulte también

interp1 | pchip | makima | ppval