La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

Factibilidad utilizando la tarea Optimize basada en problemas de Live Editor

Descripción del problema

Este ejemplo muestra cómo encontrar un punto factible mediante la tarea Optimize de Live Editor utilizando diversos solvers. El problema consiste en encontrar $$[x,y]$$ que satisfaga estas restricciones:

$$(y+x^2{)}^2+0.1y^2\le 1$$

$$y\le \exp (-x)-3$$

$$y\le x-4$$.

Represente gráficamente las curvas en las que las funciones de restricción son iguales a cero. Para ver qué parte de la región es factible (valor negativo de la función de restricción), represente las curvas en las que las funciones de restricción son iguales a -1/2. Use la función plotobjconstr que aparece al final de este script.

plotobjconstr

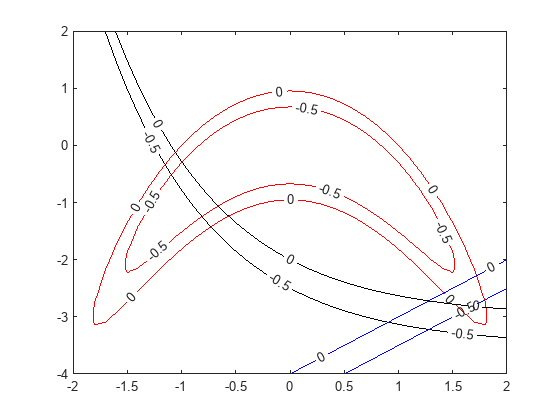
Parece haber una pequeña región factible cerca de $$x=1.75,y=-3$$. Observe que no hay ningún punto en el que todos los valores de las restricciones sean inferiores a -1/2, por lo que el conjunto factible es pequeño.

Usar la tarea Optimize basada en problemas de Live Editor

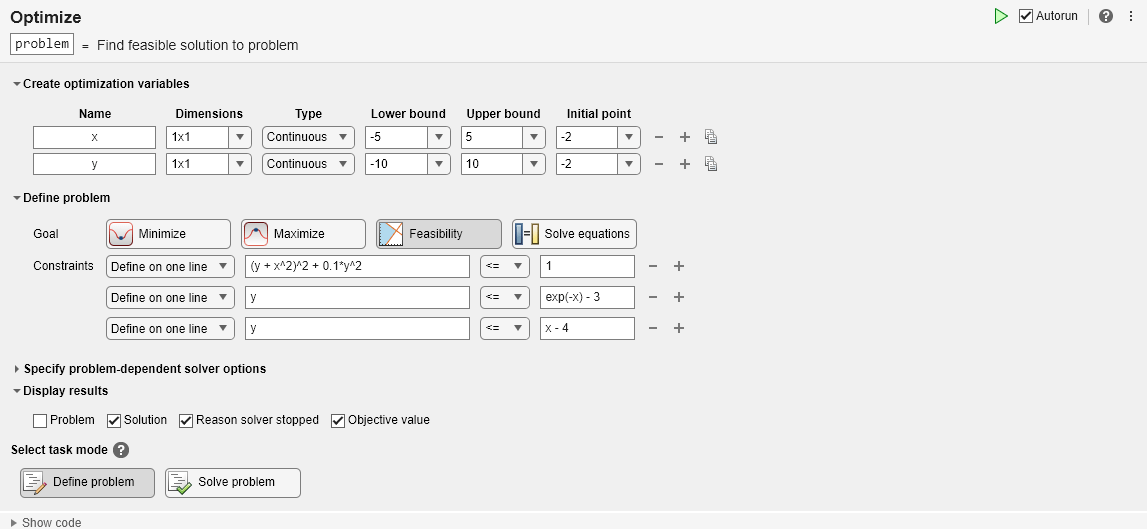
Para encontrar un punto factible, inicie la tarea Optimize de Live Editor desde un script en vivo seleccionando Task > Optimize en la pestaña Code o Insert. Elija la tarea basada en problemas.

Establezca que la variable del problema x tenga un límite inferior -5 y un límite superior 5. Establezca que la variable del problema y tenga un límite inferior -10 y un límite superior 10. Establezca el punto inicial para x en 2 y para y en -2.

Establezca Goal en Feasibility.

Cree desigualdades que representen las tres restricciones. La tarea debe coincidir con esta imagen.

Cambie el modo de tarea a Solve problem. La tarea elige el solver fmincon y llega a la siguiente solución.

Efecto del punto inicial

Partir de un punto inicial diferente puede hacer que fmincon no encuentre una solución. Establezca el punto inicial de x en -2.

Esta vez fmincon no encuentra una solución factible.

Probar un solver diferente

Para intentar encontrar una solución, pruebe con otro solver. Establezca el solver en ga. Para ello, especifique el solver en el expansor Specify problem-dependent solver options. Para monitorizar el progreso del solver, establezca la función de gráfica en Max constraint violation.

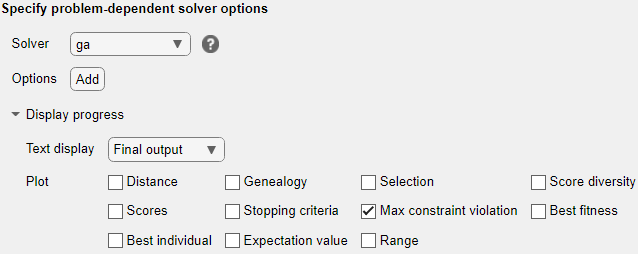
ga encuentra un punto factible dentro de la tolerancia de restricción.

ga encuentra una solución diferente a fmincon. La solución es poco factible. Para obtener una solución con menor infactibilidad, puede establecer la opción de tolerancia de la restricción en un valor inferior al predeterminado. También puede probar con otro solver.

Probar surrogateopt

Pruebe a usar el solver surrogateopt. Establezca la función de gráfica como Max constraint violation; este ajuste no se traspasa automáticamente desde la solución ga.

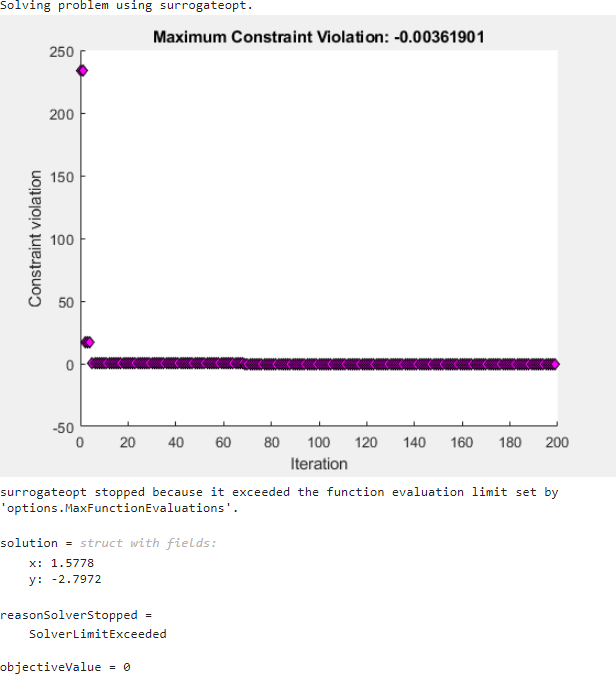
surrogateopt alcanza una solución factible, pero no se detiene cuando alcanza por primera vez una solución. En cambio, surrogateopt continúa iterando hasta que alcanza su límite de evaluación de funciones. Para detener las iteraciones antes, especifique una función de salida que detenga el solver en cuanto la vulneración de la restricción máxima alcance 1e-6 o menos. Si lo hace, el solver se detendrá mucho antes. Utilice la función auxiliar surrout, que aparece al final de este script. Para especificar esta función, cree un identificador para la función.

outfun = @surrout;

Especifique este identificador de función en el menú desplegable Specify problem-dependent solver options > Options > Diagnostics > Output function.

Esta vez el solver se detiene después de unas 30 evaluaciones de la función en lugar de 200. La solución es un poco diferente de la anterior, pero ambas son factibles.

Conclusiones

La tarea Optimize basada en problemas de Live Editor le ayuda a probar el uso de diferentes solvers en un problema, incluso solvers que tienen diferentes sintaxis como fmincon y surrogateopt. La tarea también le ayuda a establecer funciones de gráfica y a configurar otras opciones.

La tarea aparece aquí en su estado final. Experimente con distintos solvers y opciones.

Funciones auxiliares

Este código crea la función auxiliar plotobjconstr.

function plotobjconstr
[XX,YY] = meshgrid(-2:0.1:2,-4:0.1:2);
ZZ = objconstr([XX(:),YY(:)]).Ineq;
ZZ = reshape(ZZ,[size(XX),3]);
h = figure;
ax = gca;
contour(ax,XX,YY,ZZ(:,:,1),[-1/2 0],'r','ShowText','on');
hold on
contour(ax,XX,YY,ZZ(:,:,2),[-1/2 0],'k','ShowText','on');
contour(ax,XX,YY,ZZ(:,:,3),[-1/2 0],'b','ShowText','on');
hold off
end

Este código crea la función auxiliar objconstr.

function f = objconstr(x)
c(:,1) = (x(:,2) + x(:,1).^2).^2 + 0.1*x(:,2).^2 - 1;
c(:,2) = x(:,2) - exp(-x(:,1)) + 3;
c(:,3) = x(:,2) - x(:,1) + 4;
f.Ineq = c;
end

Este código crea la función auxiliar surrout

function stop = surrout(~,optimValues,~)
stop = false;
if optimValues.constrviolation <= 1e-6 % Tolerance for constraint
    stop = true;
end
end

Consulte también

Optimize | fmincon | ga (Global Optimization Toolbox) | surrogateopt (Global Optimization Toolbox)

Temas relacionados

• Solve Nonlinear Feasibility Problem, Problem-Based
• Investigate Linear Infeasibilities
• Solve Feasibility Problem (Global Optimization Toolbox)
• Flujo de trabajo de optimización basada en problemas