Algoritmo interior-point de fmincon con matriz hessiana analítica
Este ejemplo muestra cómo utilizar la información de la derivada para hacer que el proceso de resolución sea más rápido y robusto. El algoritmo interior-point de fmincon puede aceptar una función de matriz hessiana como una entrada. Cuando proporciona una matriz hessiana, puede obtener una solución más rápida y precisa a un problema de minimización restringido.
La función auxiliar bigtoleft es una función objetivo que se hace negativa rápidamente a medida que la coordenada x(1) se convierte en negativa. Su gradiente es un vector de tres elementos. El código para la función auxiliar bigtoleft aparece al final de este ejemplo.
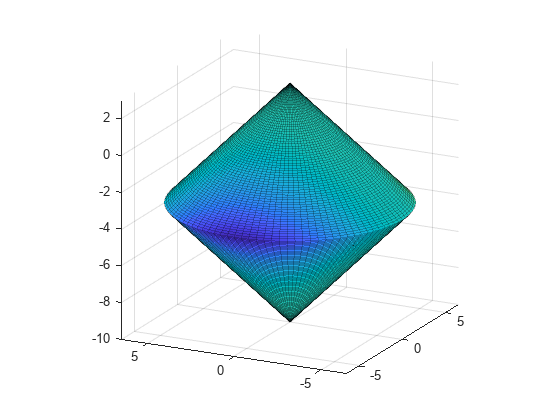
La restricción establecida para este ejemplo es la intersección de los interiores de dos conos, uno que señala hacia arriba y el otro, hacia abajo. La función de restricción es un vector de dos componentes que contiene un componente para cada cono. Puesto que este ejemplo es tridimensional, el gradiente de la restricción es una matriz de 3 por 2. El código para la función auxiliar twocone aparece al final de este ejemplo.
Cree una figura de las restricciones, coloreada utilizando la función objetivo.
% Create figure figure1 = figure; % Create axes axes1 = axes('Parent',figure1); view([-63.5 18]); grid('on'); hold('on'); % Set up polar coordinates and two cones r=0:.1:6.5; th=2*pi*(0:.01:1); x=r'*cos(th); y=r'*sin(th); z=-10+sqrt(x.^2+y.^2); zz=3-sqrt(x.^2+y.^2); % Evaluate objective function on cone surfaces newxf=reshape(bigtoleft([x(:),y(:),z(:)]),66,101)/3000; newxg=reshape(bigtoleft([x(:),y(:),z(:)]),66,101)/3000; % Create lower surf with color set by objective surf(x,y,z,newxf,'Parent',axes1,'EdgeAlpha',0.25); % Create upper surf with color set by objective surf(x,y,zz,newxg,'Parent',axes1,'EdgeAlpha',0.25); axis equal
Crear una función de matriz hessiana
Para utilizar información de la derivada de segundo orden en el solver fmincon, debe crear una matriz hessiana que sea la matriz hessiana del lagrangiano. La ecuación proporciona la matriz hessiana del lagrangiano
En este caso, es la función bigtoleft y son las funciones de restricción de dos conos. La función auxiliar hessinterior al final de este ejemplo calcula la matriz hessiana del lagrangiano en un punto x con la estructura de multiplicadores de Lagrange lambda. La primera función calcula . Después, calcula las dos matrices hessianas de restricción y , las multiplica por sus correspondientes multiplicadores de Lagrange lambda.ineqnonlin(1) y lambda.ineqnonlin(2) y las suma. En la definición de la función de restricción twocone puede ver que , lo que simplifica el cálculo.
Crear opciones para utilizar derivadas
Para permitir que fmincon utilice el gradiente objetivo, gradientes de restricción y la matriz hessiana, debe establecer las opciones adecuadas. La opción HessianFcn que utiliza la matriz hessiana del lagrangiano solo está disponible para el algoritmo interior-point.
options = optimoptions('fmincon','Algorithm','interior-point',... "SpecifyConstraintGradient",true,"SpecifyObjectiveGradient",true,... 'HessianFcn',@hessinterior);
Minimizar utilizando toda la información de las derivadas
Establezca el punto inicial x0 = [-1,-1,-1].
x0 = [-1,-1,-1];
El problema no presenta restricciones lineales ni límites. Establezca esos argumentos en [].
A = []; b = []; Aeq = []; beq = []; lb = []; ub = [];
Resuelva el problema.
[x,fval,eflag,output] = fmincon(@bigtoleft,x0,...
A,b,Aeq,beq,lb,ub,@twocone,options);Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
Examinar la solución y el proceso de resolución
Examine la solución, el valor de la función objetivo, el indicador de salida y el número de evaluaciones de función y de iteraciones.
disp(x)
-6.5000 -0.0000 -3.5000
disp(fval)
-2.8941e+03
disp(eflag)
1
disp([output.funcCount,output.iterations])
7 6
Si no utiliza una función de matriz hessiana, fmincon necesita más iteraciones para convergir y requiere más evaluaciones de función.
options.HessianFcn = [];
[x2,fval2,eflag2,output2] = fmincon(@bigtoleft,x0,...
A,b,Aeq,beq,lb,ub,@twocone,options);Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
disp([output2.funcCount,output2.iterations])
13 9
Si tampoco incluye la información de gradiente, fmincon necesita el mismo número de iteraciones, pero requiere muchas más evaluaciones de función.
options.SpecifyConstraintGradient = false;
options.SpecifyObjectiveGradient = false;
[x3,fval3,eflag3,output3] = fmincon(@bigtoleft,x0,...
A,b,Aeq,beq,lb,ub,@twocone,options);Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
disp([output3.funcCount,output3.iterations])
43 9
Funciones auxiliares
Este código crea la función auxiliar bigtoleft.
function [f gradf] = bigtoleft(x) % This is a simple function that grows rapidly negative % as x(1) becomes negative % f = 10*x(:,1).^3+x(:,1).*x(:,2).^2+x(:,3).*(x(:,1).^2+x(:,2).^2); if nargout > 1 gradf=[30*x(1)^2+x(2)^2+2*x(3)*x(1); 2*x(1)*x(2)+2*x(3)*x(2); (x(1)^2+x(2)^2)]; end end
Este código crea la función auxiliar twocone.
function [c ceq gradc gradceq] = twocone(x) % This constraint is two cones, z > -10 + r % and z < 3 - r ceq = []; r = sqrt(x(1)^2 + x(2)^2); c = [-10+r-x(3); x(3)-3+r]; if nargout > 2 gradceq = []; gradc = [x(1)/r,x(1)/r; x(2)/r,x(2)/r; -1,1]; end end
Este código crea la función auxiliar hessinterior.
function h = hessinterior(x,lambda) h = [60*x(1)+2*x(3),2*x(2),2*x(1); 2*x(2),2*(x(1)+x(3)),2*x(2); 2*x(1),2*x(2),0];% Hessian of f r = sqrt(x(1)^2+x(2)^2);% radius rinv3 = 1/r^3; hessc = [(x(2))^2*rinv3,-x(1)*x(2)*rinv3,0; -x(1)*x(2)*rinv3,x(1)^2*rinv3,0; 0,0,0];% Hessian of both c(1) and c(2) h = h + lambda.ineqnonlin(1)*hessc + lambda.ineqnonlin(2)*hessc; end