validatemodel
Validate quality of compact credit scorecard model
Syntax
Description
Stats = validatemodel(csc,data)compactCreditScorecard model for the data set specified using
the argument data.
[
specifies options using one or more name-value pair arguments in addition to
the input arguments in the previous syntax and returns the outputs
Stats,T]
= validatemodel(___,Name,Value)Stats and T.
[
specifies options using one or more name-value pair arguments in addition to
the input arguments in the previous syntax and returns the outputs
Stats,T,hf]
= validatemodel(___,Name,Value)Stats and T and the figure
handle hf to the CAP, ROC, and KS plots.
Examples
Compute model validation statistics for a compact credit scorecard model.
To create a compactCreditScorecard object, you must first develop a credit scorecard model using a creditscorecard object.
Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011).
load CreditCardData.mat sc = creditscorecard(data, 'IDVar','CustID')
sc =
creditscorecard with properties:
GoodLabel: 0
ResponseVar: 'status'
WeightsVar: ''
VarNames: {'CustID' 'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate' 'status'}
NumericPredictors: {'CustAge' 'TmAtAddress' 'CustIncome' 'TmWBank' 'AMBalance' 'UtilRate'}
CategoricalPredictors: {'ResStatus' 'EmpStatus' 'OtherCC'}
BinMissingData: 0
IDVar: 'CustID'
PredictorVars: {'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate'}
Data: [1200×11 table]
Perform automatic binning using the default options. By default, autobinning uses the Monotone algorithm.
sc = autobinning(sc);
Fit the model.
sc = fitmodel(sc);
1. Adding CustIncome, Deviance = 1490.8527, Chi2Stat = 32.588614, PValue = 1.1387992e-08
2. Adding TmWBank, Deviance = 1467.1415, Chi2Stat = 23.711203, PValue = 1.1192909e-06
3. Adding AMBalance, Deviance = 1455.5715, Chi2Stat = 11.569967, PValue = 0.00067025601
4. Adding EmpStatus, Deviance = 1447.3451, Chi2Stat = 8.2264038, PValue = 0.0041285257
5. Adding CustAge, Deviance = 1441.994, Chi2Stat = 5.3511754, PValue = 0.020708306
6. Adding ResStatus, Deviance = 1437.8756, Chi2Stat = 4.118404, PValue = 0.042419078
7. Adding OtherCC, Deviance = 1433.707, Chi2Stat = 4.1686018, PValue = 0.041179769
Generalized linear regression model:
logit(status) ~ 1 + CustAge + ResStatus + EmpStatus + CustIncome + TmWBank + OtherCC + AMBalance
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ ______ __________
(Intercept) 0.70239 0.064001 10.975 5.0538e-28
CustAge 0.60833 0.24932 2.44 0.014687
ResStatus 1.377 0.65272 2.1097 0.034888
EmpStatus 0.88565 0.293 3.0227 0.0025055
CustIncome 0.70164 0.21844 3.2121 0.0013179
TmWBank 1.1074 0.23271 4.7589 1.9464e-06
OtherCC 1.0883 0.52912 2.0569 0.039696
AMBalance 1.045 0.32214 3.2439 0.0011792
1200 observations, 1192 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 89.7, p-value = 1.4e-16
Format the unscaled points.
sc = formatpoints(sc, 'PointsOddsAndPDO',[500,2,50]);Convert the creditscorecard object into a compactCreditScorecard object. A compactCreditScorecard object is a lightweight version of a creditscorecard object that is used for deployment purposes.
csc = compactCreditScorecard(sc);
Validate the compact credit scorecard model by generating the CAP, ROC, and KS plots. This example uses the training data. However, you can use any validation data, as long as:
The data has the same predictor names and predictor types as the data used to create the initial
creditscorecardobject.The data has a response column with the same name as the
'ResponseVar'property in the initialcreditscorecardobject.The data has a weights column (if weights were used to train the model) with the same name as
'WeightsVar'property in the initialcreditscorecardobject.
[Stats,T] = validatemodel(csc,data,'Plot',{'CAP','ROC','KS'});
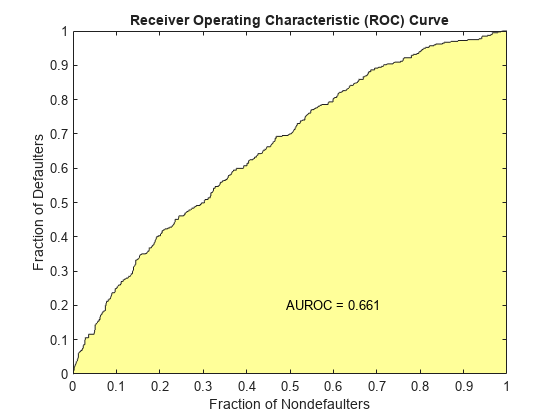
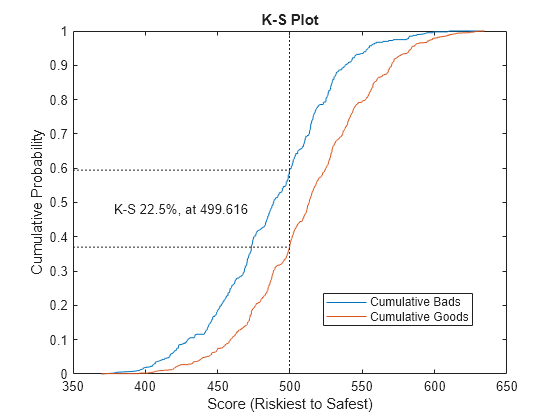
disp(Stats)
Measure Value
________________________ _______
{'Accuracy Ratio' } 0.32258
{'Area under ROC curve'} 0.66129
{'KS statistic' } 0.2246
{'KS score' } 499.62
disp(T(1:15,:))
Scores ProbDefault TrueBads FalseBads TrueGoods FalseGoods Sensitivity FalseAlarm PctObs
______ ___________ ________ _________ _________ __________ ___________ __________ __________
369.54 0.75313 0 1 802 397 0 0.0012453 0.00083333
378.19 0.73016 1 1 802 396 0.0025189 0.0012453 0.0016667
380.28 0.72444 2 1 802 395 0.0050378 0.0012453 0.0025
391.49 0.69234 3 1 802 394 0.0075567 0.0012453 0.0033333
395.57 0.68017 4 1 802 393 0.010076 0.0012453 0.0041667
396.14 0.67846 4 2 801 393 0.010076 0.0024907 0.005
396.45 0.67752 5 2 801 392 0.012594 0.0024907 0.0058333
398.61 0.67094 6 2 801 391 0.015113 0.0024907 0.0066667
398.68 0.67072 7 2 801 390 0.017632 0.0024907 0.0075
401.33 0.66255 8 2 801 389 0.020151 0.0024907 0.0083333
402.66 0.65842 8 3 800 389 0.020151 0.003736 0.0091667
404.25 0.65346 9 3 800 388 0.02267 0.003736 0.01
404.73 0.65193 9 4 799 388 0.02267 0.0049813 0.010833
405.53 0.64941 11 4 799 386 0.027708 0.0049813 0.0125
405.7 0.64887 11 5 798 386 0.027708 0.0062267 0.013333
Compute model validation statistics for a compact credit scorecard model with weights.
To create a compactCreditScorecard object, you must first develop a credit scorecard model using a creditscorecard object.
Use the CreditCardData.mat file to load the data (dataWeights) that contains a column (RowWeights) for the weights (using a dataset from Refaat 2011).
load CreditCardData.matCreate a creditscorecard object using the optional name-value pair argument 'WeightsVar'.
sc = creditscorecard(dataWeights,'IDVar','CustID','WeightsVar','RowWeights')
sc =
creditscorecard with properties:
GoodLabel: 0
ResponseVar: 'status'
WeightsVar: 'RowWeights'
VarNames: {'CustID' 'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate' 'RowWeights' 'status'}
NumericPredictors: {'CustAge' 'TmAtAddress' 'CustIncome' 'TmWBank' 'AMBalance' 'UtilRate'}
CategoricalPredictors: {'ResStatus' 'EmpStatus' 'OtherCC'}
BinMissingData: 0
IDVar: 'CustID'
PredictorVars: {'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate'}
Data: [1200×12 table]
Perform automatic binning. By default, autobinning uses the Monotone algorithm.
sc = autobinning(sc)
sc =
creditscorecard with properties:
GoodLabel: 0
ResponseVar: 'status'
WeightsVar: 'RowWeights'
VarNames: {'CustID' 'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate' 'RowWeights' 'status'}
NumericPredictors: {'CustAge' 'TmAtAddress' 'CustIncome' 'TmWBank' 'AMBalance' 'UtilRate'}
CategoricalPredictors: {'ResStatus' 'EmpStatus' 'OtherCC'}
BinMissingData: 0
IDVar: 'CustID'
PredictorVars: {'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate'}
Data: [1200×12 table]
Fit the model.
sc = fitmodel(sc);
1. Adding CustIncome, Deviance = 764.3187, Chi2Stat = 15.81927, PValue = 6.968927e-05
2. Adding TmWBank, Deviance = 751.0215, Chi2Stat = 13.29726, PValue = 0.0002657942
3. Adding AMBalance, Deviance = 743.7581, Chi2Stat = 7.263384, PValue = 0.007037455
Generalized linear regression model:
logit(status) ~ 1 + CustIncome + TmWBank + AMBalance
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ ______ __________
(Intercept) 0.70642 0.088702 7.964 1.6653e-15
CustIncome 1.0268 0.25758 3.9862 6.7132e-05
TmWBank 1.0973 0.31294 3.5063 0.0004543
AMBalance 1.0039 0.37576 2.6717 0.0075464
1200 observations, 1196 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 36.4, p-value = 6.22e-08
Format the unscaled points.
sc = formatpoints(sc,'PointsOddsAndPDO',[500,2,50]);Convert the creditscorecard object into a compactCreditScorecard object. A compactCreditScorecard object is a lightweight version of a creditscorecard object that is used for deployment purposes.
csc = compactCreditScorecard(sc);
Validate the compact credit scorecard model by generating the CAP, ROC, and KS plots. When you use the optional name-value pair argument 'WeightsVar' to specify observation (sample) weights in the original creditscorecard object, the T table for validatemodel uses statistics, sums, and cumulative sums that are weighted counts.
This example uses the training data (dataWeights). However, you can use any validation data, as long as:
The data has the same predictor names and predictor types as the data used to create the initial
creditscorecardobject.The data has a response column with the same name as the
'ResponseVar'property in the initialcreditscorecardobject.The data has a weights column (if weights were used to train the model) with the same name as the
'WeightsVar'property in the initialcreditscorecardobject.
[Stats,T] = validatemodel(csc,dataWeights,'Plot',{'CAP','ROC','KS'});
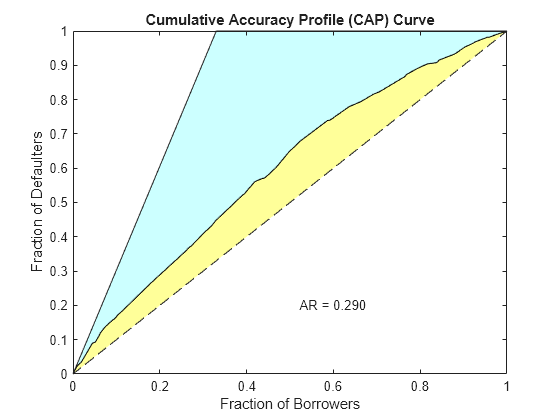
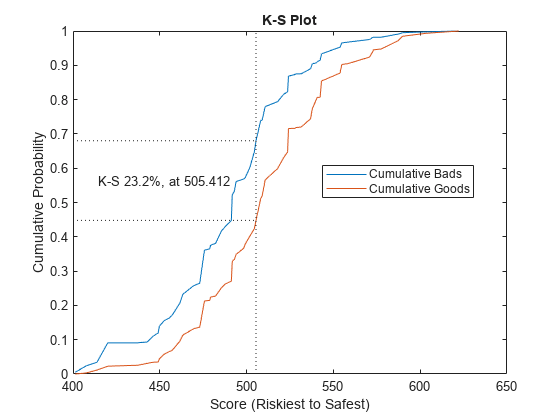
Stats
Stats=4×2 table
Measure Value
________________________ _______
{'Accuracy Ratio' } 0.28972
{'Area under ROC curve'} 0.64486
{'KS statistic' } 0.23215
{'KS score' } 505.41
T(1:10,:)
ans=10×9 table
Scores ProbDefault TrueBads FalseBads TrueGoods FalseGoods Sensitivity FalseAlarm PctObs
______ ___________ ________ _________ _________ __________ ___________ __________ _________
401.34 0.66253 1.0788 0 411.95 201.95 0.0053135 0 0.0017542
407.59 0.64289 4.8363 1.2768 410.67 198.19 0.023821 0.0030995 0.0099405
413.79 0.62292 6.9469 4.6942 407.25 196.08 0.034216 0.011395 0.018929
420.04 0.60236 18.459 9.3899 402.56 184.57 0.090918 0.022794 0.045285
437.27 0.544 18.459 10.514 401.43 184.57 0.090918 0.025523 0.047113
442.83 0.52481 18.973 12.794 399.15 184.06 0.093448 0.031057 0.051655
446.19 0.51319 22.396 14.15 397.8 180.64 0.11031 0.034349 0.059426
449.08 0.50317 24.325 14.405 397.54 178.71 0.11981 0.034968 0.062978
449.73 0.50095 28.246 18.049 393.9 174.78 0.13912 0.043813 0.075279
452.44 0.49153 31.511 23.565 388.38 171.52 0.1552 0.057204 0.089557
Compute model validation statistics and assign points for missing data when using the 'BinMissingData' option.
Predictors in a
creditscorecardobject that have missing data in the training set have an explicit bin for<missing>with corresponding points in the final scorecard. These points are computed from the Weight-of-Evidence (WOE) value for the<missing>bin and the logistic model coefficients. For scoring purposes, these points are assigned to missing values and to out-of-range values, and after you convert thecreditscorecardobject to acompactCreditScorecardobject, you can use the final score to compute model validation statistics withvalidatemodel.Predictors in a
creditscorecardobject with no missing data in the training set have no<missing>bin, so no WOE can be estimated from the training data. By default, the points for missing and out-of-range values are set toNaNresulting in a score ofNaNwhen runningscore. For predictors in acreditscorecardobject that have no explicit<missing>bin, use the name-value argument'Missing'informatpointsto specify how the function treats missing data for scoring purposes. After converting thecreditscorecardobject to acompactCreditScorecardobject, you can use the final score to compute model validation statistics withvalidatemodel.
To create a compactCreditScorecard object, you must first develop a credit scorecard model using a creditscorecard object.
Create a creditscorecard object using the CreditCardData.mat file to load dataMissing, a table that contains missing values.
load CreditCardData.mat
head(dataMissing,5) CustID CustAge TmAtAddress ResStatus EmpStatus CustIncome TmWBank OtherCC AMBalance UtilRate status
______ _______ ___________ ___________ _________ __________ _______ _______ _________ ________ ______
1 53 62 <undefined> Unknown 50000 55 Yes 1055.9 0.22 0
2 61 22 Home Owner Employed 52000 25 Yes 1161.6 0.24 0
3 47 30 Tenant Employed 37000 61 No 877.23 0.29 0
4 NaN 75 Home Owner Employed 53000 20 Yes 157.37 0.08 0
5 68 56 Home Owner Employed 53000 14 Yes 561.84 0.11 0
Use creditscorecard with the name-value argument 'BinMissingData' set to true to bin the missing numeric or categorical data in a separate bin. Apply automatic binning.
sc = creditscorecard(dataMissing,'IDVar','CustID','BinMissingData',true); sc = autobinning(sc); disp(sc)
creditscorecard with properties:
GoodLabel: 0
ResponseVar: 'status'
WeightsVar: ''
VarNames: {'CustID' 'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate' 'status'}
NumericPredictors: {'CustAge' 'TmAtAddress' 'CustIncome' 'TmWBank' 'AMBalance' 'UtilRate'}
CategoricalPredictors: {'ResStatus' 'EmpStatus' 'OtherCC'}
BinMissingData: 1
IDVar: 'CustID'
PredictorVars: {'CustAge' 'TmAtAddress' 'ResStatus' 'EmpStatus' 'CustIncome' 'TmWBank' 'OtherCC' 'AMBalance' 'UtilRate'}
Data: [1200×11 table]
To make any negative age or income information invalid or "out of range," set a minimum value of zero for 'CustAge' and 'CustIncome'. For scoring and probability-of-default computations, out-of-range values are given the same points as missing values.
sc = modifybins(sc,'CustAge','MinValue',0); sc = modifybins(sc,'CustIncome','MinValue',0);
Display bin information for numeric data for 'CustAge' that includes missing data in a separate bin labelled <missing>.
bi = bininfo(sc,'CustAge');
disp(bi) Bin Good Bad Odds WOE InfoValue
_____________ ____ ___ ______ ________ __________
{'[0,33)' } 69 52 1.3269 -0.42156 0.018993
{'[33,37)' } 63 45 1.4 -0.36795 0.012839
{'[37,40)' } 72 47 1.5319 -0.2779 0.0079824
{'[40,46)' } 172 89 1.9326 -0.04556 0.0004549
{'[46,48)' } 59 25 2.36 0.15424 0.0016199
{'[48,51)' } 99 41 2.4146 0.17713 0.0035449
{'[51,58)' } 157 62 2.5323 0.22469 0.0088407
{'[58,Inf]' } 93 25 3.72 0.60931 0.032198
{'<missing>'} 19 11 1.7273 -0.15787 0.00063885
{'Totals' } 803 397 2.0227 NaN 0.087112
Display bin information for categorical data for 'ResStatus' that includes missing data in a separate bin labelled <missing>.
bi = bininfo(sc,'ResStatus');
disp(bi) Bin Good Bad Odds WOE InfoValue
______________ ____ ___ ______ _________ __________
{'Tenant' } 296 161 1.8385 -0.095463 0.0035249
{'Home Owner'} 352 171 2.0585 0.017549 0.00013382
{'Other' } 128 52 2.4615 0.19637 0.0055808
{'<missing>' } 27 13 2.0769 0.026469 2.3248e-05
{'Totals' } 803 397 2.0227 NaN 0.0092627
For the 'CustAge' and 'ResStatus' predictors, the training data contains missing data (NaNs and <undefined> values. For missing data in these predictors, the binning process estimates WOE values of -0.15787 and 0.026469, respectively.
Because the training data contains no missing values for the 'EmpStatus' and 'CustIncome' predictors, neither predictor has an explicit bin for missing values.
bi = bininfo(sc,'EmpStatus');
disp(bi) Bin Good Bad Odds WOE InfoValue
____________ ____ ___ ______ ________ _________
{'Unknown' } 396 239 1.6569 -0.19947 0.021715
{'Employed'} 407 158 2.5759 0.2418 0.026323
{'Totals' } 803 397 2.0227 NaN 0.048038
bi = bininfo(sc,'CustIncome');
disp(bi) Bin Good Bad Odds WOE InfoValue
_________________ ____ ___ _______ _________ __________
{'[0,29000)' } 53 58 0.91379 -0.79457 0.06364
{'[29000,33000)'} 74 49 1.5102 -0.29217 0.0091366
{'[33000,35000)'} 68 36 1.8889 -0.06843 0.00041042
{'[35000,40000)'} 193 98 1.9694 -0.026696 0.00017359
{'[40000,42000)'} 68 34 2 -0.011271 1.0819e-05
{'[42000,47000)'} 164 66 2.4848 0.20579 0.0078175
{'[47000,Inf]' } 183 56 3.2679 0.47972 0.041657
{'Totals' } 803 397 2.0227 NaN 0.12285
Use fitmodel to fit a logistic regression model using Weight of Evidence (WOE) data. fitmodel internally transforms all the predictor variables into WOE values by using the bins found in the automatic binning process. fitmodel then fits a logistic regression model using a stepwise method (by default). For predictors that have missing data, there is an explicit <missing> bin, with a corresponding WOE value computed from the data. When you use fitmodel, the function applies the corresponding WOE value for the <missing> bin when performing the WOE transformation.
[sc,mdl] = fitmodel(sc);
1. Adding CustIncome, Deviance = 1490.8527, Chi2Stat = 32.588614, PValue = 1.1387992e-08
2. Adding TmWBank, Deviance = 1467.1415, Chi2Stat = 23.711203, PValue = 1.1192909e-06
3. Adding AMBalance, Deviance = 1455.5715, Chi2Stat = 11.569967, PValue = 0.00067025601
4. Adding EmpStatus, Deviance = 1447.3451, Chi2Stat = 8.2264038, PValue = 0.0041285257
5. Adding CustAge, Deviance = 1442.8477, Chi2Stat = 4.4974731, PValue = 0.033944979
6. Adding ResStatus, Deviance = 1438.9783, Chi2Stat = 3.86941, PValue = 0.049173805
7. Adding OtherCC, Deviance = 1434.9751, Chi2Stat = 4.0031966, PValue = 0.045414057
Generalized linear regression model:
logit(status) ~ 1 + CustAge + ResStatus + EmpStatus + CustIncome + TmWBank + OtherCC + AMBalance
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ ______ __________
(Intercept) 0.70229 0.063959 10.98 4.7498e-28
CustAge 0.57421 0.25708 2.2335 0.025513
ResStatus 1.3629 0.66952 2.0356 0.04179
EmpStatus 0.88373 0.2929 3.0172 0.002551
CustIncome 0.73535 0.2159 3.406 0.00065929
TmWBank 1.1065 0.23267 4.7556 1.9783e-06
OtherCC 1.0648 0.52826 2.0156 0.043841
AMBalance 1.0446 0.32197 3.2443 0.0011775
1200 observations, 1192 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 88.5, p-value = 2.55e-16
Scale the scorecard points by the "points, odds, and points to double the odds (PDO)" method using the 'PointsOddsAndPDO' argument of formatpoints. Suppose that you want a score of 500 points to have odds of 2 (twice as likely to be good than to be bad) and that the odds double every 50 points (so that 550 points would have odds of 4).
Display the scorecard showing the scaled points for predictors retained in the fitting model.
sc = formatpoints(sc,'PointsOddsAndPDO',[500 2 50]);
PointsInfo = displaypoints(sc)PointsInfo=38×3 table
Predictors Bin Points
_____________ ______________ ______
{'CustAge' } {'[0,33)' } 54.062
{'CustAge' } {'[33,37)' } 56.282
{'CustAge' } {'[37,40)' } 60.012
{'CustAge' } {'[40,46)' } 69.636
{'CustAge' } {'[46,48)' } 77.912
{'CustAge' } {'[48,51)' } 78.86
{'CustAge' } {'[51,58)' } 80.83
{'CustAge' } {'[58,Inf]' } 96.76
{'CustAge' } {'<missing>' } 64.984
{'ResStatus'} {'Tenant' } 62.138
{'ResStatus'} {'Home Owner'} 73.248
{'ResStatus'} {'Other' } 90.828
{'ResStatus'} {'<missing>' } 74.125
{'EmpStatus'} {'Unknown' } 58.807
{'EmpStatus'} {'Employed' } 86.937
{'EmpStatus'} {'<missing>' } NaN
⋮
Notice that points for the <missing> bin for 'CustAge' and 'ResStatus' are explicitly shown (as 64.9836 and 74.1250, respectively). The function computes these points from the WOE value for the <missing> bin and the logistic model coefficients.
For predictors that have no missing data in the training set, there is no explicit <missing> bin during the training of the model. By default, displaypoints reports the points as NaN for missing data resulting in a score of NaN when you use score. For these predictors, use the name-value pair argument 'Missing' in formatpoints to indicate how missing data should be treated for scoring purposes.
Use compactCreditScorecard to convert the creditscorecard object into a compactCreditScorecard object. A compactCreditScorecard object is a lightweight version of a creditscorecard object that is used for deployment purposes.
csc = compactCreditScorecard(sc);
For the purpose of illustration, take a few rows from the original data as test data and introduce some missing data. Also introduce some invalid, or out-of-range, values. For numeric data, values below the minimum (or above the maximum) are considered invalid, such as a negative value for age (recall that in a previous step, you set 'MinValue' to 0 for 'CustAge' and 'CustIncome'). For categorical data, invalid values are categories not explicitly included in the scorecard, for example, a residential status not previously mapped to scorecard categories, such as "House", or a meaningless string such as "abc123."
This example uses a very small validation data set only to illustrate the scoring of rows with missing and out-of-range values and the relationship between scoring and model validation.
tdata = dataMissing(11:200,mdl.PredictorNames); % Keep only the predictors retained in the model tdata.status = dataMissing.status(11:200); % Copy the response variable value, needed for validation purposes % Set some missing values tdata.CustAge(1) = NaN; tdata.ResStatus(2) = missing; tdata.EmpStatus(3) = missing; tdata.CustIncome(4) = NaN; % Set some invalid values tdata.CustAge(5) = -100; tdata.ResStatus(6) = 'House'; tdata.EmpStatus(7) = 'Freelancer'; tdata.CustIncome(8) = -1; disp(tdata(1:10,:))
CustAge ResStatus EmpStatus CustIncome TmWBank OtherCC AMBalance status
_______ ___________ ___________ __________ _______ _______ _________ ______
NaN Tenant Unknown 34000 44 Yes 119.8 1
48 <undefined> Unknown 44000 14 Yes 403.62 0
65 Home Owner <undefined> 48000 6 No 111.88 0
44 Other Unknown NaN 35 No 436.41 0
-100 Other Employed 46000 16 Yes 162.21 0
33 House Employed 36000 36 Yes 845.02 0
39 Tenant Freelancer 34000 40 Yes 756.26 1
24 Home Owner Employed -1 19 Yes 449.61 0
NaN Home Owner Employed 51000 11 Yes 519.46 1
52 Other Unknown 42000 12 Yes 1269.2 0
Use validatemodel for a compactCreditScorecard object with the validation data set (tdata).
[ValStats,ValTable] = validatemodel(csc,tdata,'Plot',{'CAP','ROC','KS'});
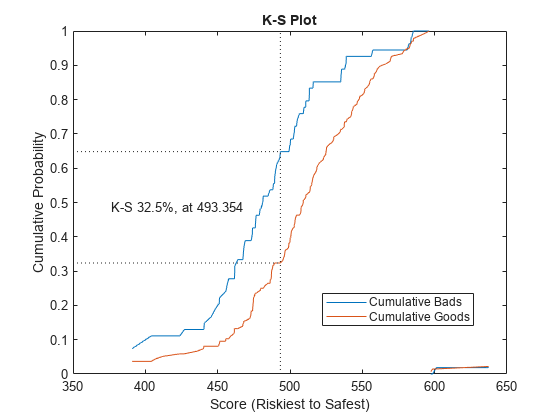
disp(ValStats)
Measure Value
________________________ _______
{'Accuracy Ratio' } 0.35376
{'Area under ROC curve'} 0.67688
{'KS statistic' } 0.32462
{'KS score' } 493.35
disp(ValTable(1:10,:))
Scores ProbDefault TrueBads FalseBads TrueGoods FalseGoods Sensitivity FalseAlarm PctObs
______ ___________ ________ _________ _________ __________ ___________ __________ _________
597.33 NaN 0 1 135 54 0 0.0073529 0.0052632
598.54 NaN 0 2 134 54 0 0.014706 0.010526
601.18 NaN 1 2 134 53 0.018519 0.014706 0.015789
637.3 NaN 1 3 133 53 0.018519 0.022059 0.021053
NaN 0.69421 2 3 133 52 0.037037 0.022059 0.026316
NaN 0.65394 2 4 132 52 0.037037 0.029412 0.031579
NaN 0.64441 2 5 131 52 0.037037 0.036765 0.036842
NaN 0.62799 3 5 131 51 0.055556 0.036765 0.042105
390.86 0.58964 4 5 131 50 0.074074 0.036765 0.047368
404.09 0.57902 6 5 131 48 0.11111 0.036765 0.057895
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] “Basel Committee on Banking Supervision: Studies on the Validation of Internal Rating Systems.” Working Paper No. 14, February 2005.
[2] Refaat, M. Credit Risk Scorecards: Development and Implementation Using SAS. lulu.com, 2011.
[3] Loeffler, G. and P. N. Posch. Credit Risk Modeling Using Excel and VBA. Wiley Finance, 2007.
Version History
Introduced in R2019b
