La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

rcosdesign

Diseño de filtros FIR de impulsos de coseno alzado

Sintaxis

b = rcosdesign(beta,span,sps)

b = rcosdesign(beta,span,sps,shape)

Descripción

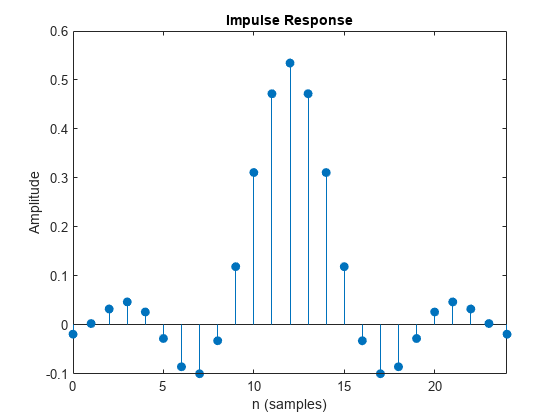
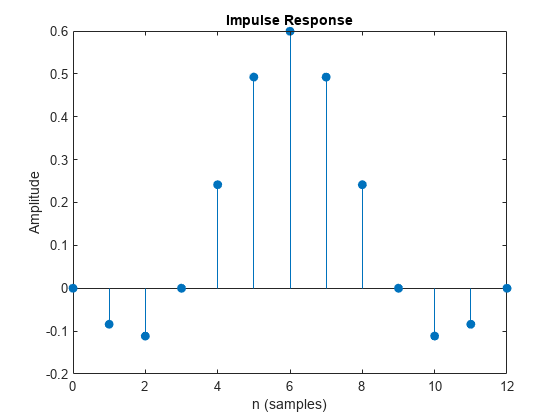
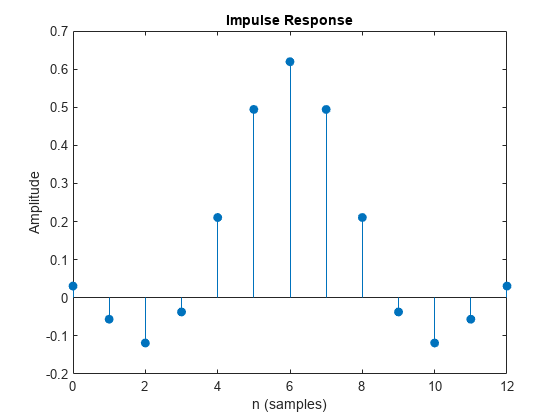
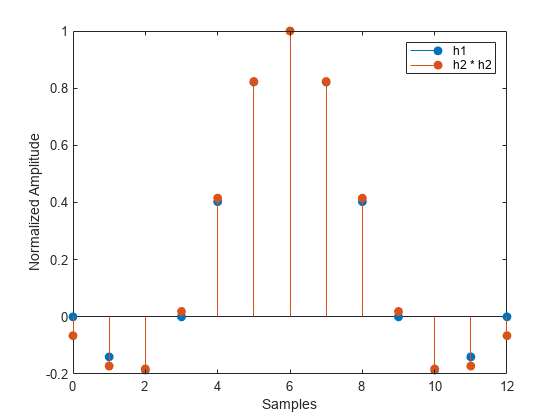
b = rcosdesign(beta,span,sps) devuelve los coeficientes b, que corresponden a un filtro FIR de coseno alzado de raíz cuadrada con el factor de descenso especificado por beta. El filtro se compone de símbolos span. Cada periodo del símbolo contiene muestras de sps. El orden del filtro, sps*span, debe ser par. La energía de filtro es 1.

b = rcosdesign(beta,span,sps,shape) devuelve un filtro de coseno alzado de raíz cuadrada al establecer shape en "sqrt" y un filtro FIR de coseno alzado normal al establecer shape en "normal".

Ejemplos

Diseñar un filtro de coseno alzado de raíz cuadrada

Especifique un factor de descenso de 0,25. Asocie el filtro a 6 símbolos y represente cada símbolo con 4 muestras. Compruebe que 'sqrt' es el valor predeterminado del parámetro shape.

h = rcosdesign(0.25,6,4);
mx = max(abs(h-rcosdesign(0.25,6,4,'sqrt')))

mx = 0

fvtool(h,'Analysis','impulse')

Respuestas al impulso de filtros de coseno alzado normales y de raíz cuadrada

Compare un filtro de coseno alzado normal con un filtro de coseno alzado de raíz cuadrada. Un filtro de impulsos de coseno alzado normal (de longitud infinita) ideal equivale a dos filtros de coseno alzado de raíz cuadrada ideales en cascada. Así, la respuesta al impulso de un filtro FIR normal debe parecerse a la de un filtro de raíz cuadrada convolucionado consigo mismo.

Cree un filtro de coseno alzado normal con descenso de 0,25. Especifique que este filtro abarca 4 símbolos con 3 muestras por símbolo.

rf = 0.25;
span = 4;
sps = 3;

h1 = rcosdesign(rf,span,sps,"normal");
impz(h1)

El filtro normal tiene cruces por cero en los múltiplos enteros de sps. Por lo tanto, satisface el criterio de Nyquist de interferencia cero entre símbolos. No es el caso, sin embargo, del filtro de raíz cuadrada:

h2 = rcosdesign(rf,span,sps,"sqrt");
impz(h2)

Convolucione el filtro de raíz cuadrada consigo mismo. Trunque la respuesta al impulso hacia fuera desde el máximo, de forma que tenga la misma longitud que h1. Normalice la respuesta utilizando el máximo. Compare el filtro de raíz cuadrada convolucionado con el filtro normal.

h3 = conv(h2,h2,"same");

stem(0:span*sps,[h1/max(abs(h1));h3/max(abs(h3))]',"filled")
xlabel("Samples")
ylabel("Normalized Amplitude")
legend("h1","h2 * h2")

La respuesta convolucionada no coincide con el filtro normal debido a su longitud finita. Aumente span para que las respuestas se acerquen más y cumplir así mejor el criterio de Nyquist.

Pasar una señal por un filtro de coseno alzado

Este ejemplo muestra cómo pasar una señal por un filtro de coseno alzado de raíz cuadrada.

Especifique los parámetros de filtro.

rolloff = 0.25;     % Rolloff factor
span = 6;           % Filter span in symbols
sps = 4;            % Samples per symbol

Genere los coeficientes del filtro de coseno alzado de raíz cuadrada.

b = rcosdesign(rolloff, span, sps);

Cree un vector de datos bipolares.

d = 2*randi([0 1], 100, 1) - 1;

Sobremuestree y filtre los datos para la conformación de pulso.

x = upfirdn(d, b, sps);

Añada ruido.

r = x + randn(size(x))*0.01;

Filtre y submuestree la señal recibida para el filtrado pertinente.

y = upfirdn(r, b, 1, sps);

Para obtener más información sobre cómo usar los filtros de coseno alzado de raíz cuadrada para interpolar y diezmar señales, consulte Interpolate and Decimate Using RRC Filter (Communications Toolbox).

Argumentos de entrada

beta — Factor de descenso

escalar real no negativo

Factor de descenso, especificado como escalar real no negativo no mayor que 1. El factor de descenso determina el ancho de banda en exceso del filtro. El descenso cero se corresponde con un filtro paso bajo y el descenso de unidad con un coseno alzado puro.

Tipos de datos: double | single

span — Número de símbolos

escalar entero positivo

Número de símbolos, especificado como un escalar entero positivo.

Tipos de datos: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

sps — Muestras por símbolo

escalar entero positivo

Número de muestras por símbolo (factor de sobremuestreo), especificado como escalar entero positivo.

Tipos de datos: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

shape — Forma de la ventana de coseno alzado

"sqrt" (predeterminado) | "normal"

Forma de la ventana de coseno alzado, especificada como "normal" o "sqrt".

Argumentos de salida

b — Coeficientes de filtro FIR

vector fila

Coeficientes del filtro de coseno alzado, devueltos como vector fila.

Tipos de datos: double

Sugerencias

• Si tiene una licencia para el software Communications Toolbox™, puede realizar filtraciones de coseno alzado multitasa con comportamiento de transmisión. Para ello, utilice los filtros System object™, comm.RaisedCosineTransmitFilter y comm.RaisedCosineReceiveFilter.

Referencias

[1] Tranter, William H., K. Sam Shanmugan, Theodore S. Rappaport, and Kurt L. Kosbar. Principles of Communication Systems Simulation with Wireless Applications. Upper Saddle River, NJ: Prentice Hall, 2004.

Capacidades ampliadas

Generación de código C/C++
Genere código C y C++ mediante MATLAB® Coder™.

Historial de versiones

Introducido en R2013b

Consulte también

gaussdesign

Temas

• Interpolate and Decimate Using RRC Filter (Communications Toolbox)