Frequency Estimation by Subspace Methods
This example shows how to resolve closely spaced sine waves using subspace methods. Subspace methods assume a harmonic model consisting of a sum of sine waves, possibly complex, in additive noise. In a complex-valued harmonic model, the noise is also complex-valued.
Create a complex-valued signal 24 samples in length. The signal consists of two complex exponentials (sine waves) with frequencies of 0.4 Hz and 0.425 Hz and additive complex white Gaussian noise. The noise has zero mean and variance . In complex white noise, both the real and imaginary parts have variance equal to one-half the overall variance.
n = 0:23;
x = exp(1j*2*pi*0.4*n) + exp(1j*2*pi*0.425*n)+ ...
0.2/sqrt(2)*(randn(size(n))+1j*randn(size(n)));Attempt to resolve the two sine waves using the power spectrum of the signal. Set the leakage to the maximum value for best results.
pspectrum(x,n,'Leakage',1)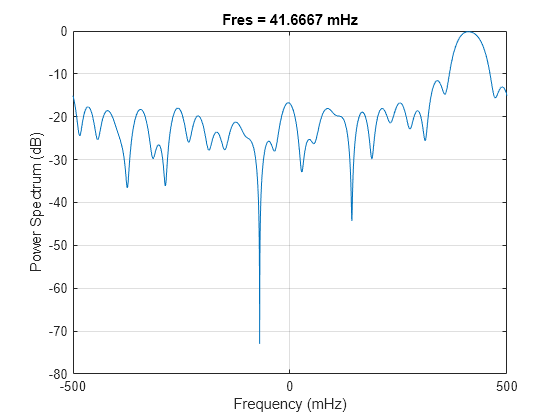
The periodogram shows a broad peak near 0.4 Hz. You cannot resolve the two separate sine waves because the frequency resolution of the periodogram is 1/N, where N is the length of the signal. In this case, 1/N is greater than the separation of the two sine waves. Zero padding does not help to resolve two separate peaks.
Use a subspace method to resolve the two closely spaced peaks. In this example, use the MUSIC method. Estimate the autocorrelation matrix and input the autocorrelation matrix into pmusic. Specify a model with two sinusoidal components. Plot the result.
[X,R] = corrmtx(x,14,'mod'); pmusic(R,2,[],1,'corr')
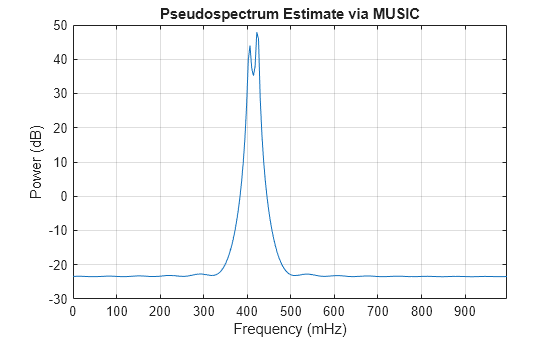
The MUSIC method is able to separate the two peaks at 0.4 Hz and 0.425 Hz. However, subspace methods do not produce power estimates like power spectral density estimates. Subspace methods are most useful for frequency identification and can be sensitive to model-order misspecification.