pspectrum

Analizar señales en los dominios de frecuencia y de tiempo-frecuencia

Sintaxis

p = pspectrum(x)

p = pspectrum(x,fs)

p = pspectrum(x,t)

p = pspectrum(___,type)

p = pspectrum(___,Name,Value)

[p,f] = pspectrum(___)

[p,f,t] = pspectrum(___,'spectrogram')

[p,f,pwr] = pspectrum(___,'persistence')

pspectrum(___)

Descripción

p = pspectrum(x) devuelve el espectro de potencia de x.

• Si x es un vector o un horario con un vector de datos, se trata como un solo canal.

• Si x es una matriz, un horario con una variable matricial o un horario con múltiples variables vectoriales, entonces el espectro se calcula independientemente para cada canal y se almacena en una columna separada de p.

p = pspectrum(x,fs) devuelve el espectro de potencia de una señal vectorial o matricial muestreada a una velocidad fs.

p = pspectrum(x,t) devuelve el espectro de potencia de una señal vectorial o matricial muestreada en los instantes de tiempo especificados en t.

p = pspectrum(___,type) especifica el tipo de análisis del espectro que realiza la función. Especifique type como 'power', 'spectrogram' o 'persistence'. Esta sintaxis puede incluir cualquier combinación de argumentos de entrada de las sintaxis anteriores.

p = pspectrum(___,Name,Value) especifica opciones adicionales con argumentos de par nombre-valor. Las opciones incluyen el ancho de banda de la resolución de frecuencia y el porcentaje de solapamiento entre segmentos contiguos.

[p,f] = pspectrum(___) devuelve las frecuencias correspondientes a las estimaciones espectrales contenidas en p.

[p,f,t] = pspectrum(___,'spectrogram') también devuelve un vector de instantes de tiempo correspondientes a los centros de los segmentos con ventana utilizados para calcular las estimaciones del espectro de potencia de tiempo corto.

[p,f,pwr] = pspectrum(___,'persistence') también devuelve un vector de valores de potencia correspondientes a las estimaciones contenidas en un espectro de persistencia.

pspectrum(___) sin argumentos de salida representa la estimación espectral en la ventana de figura actual. En la gráfica, la función convierte p en dB utilizando 10 log₁₀(p).

Ejemplos

Espectros de potencia de sinusoides

Genere 128 muestras de una sinusoide compleja de dos canales.

• El primer canal tiene una amplitud unitaria y una frecuencia sinusoidal normalizada de $\pi /4$ rad/muestra

• El segundo canal tiene una amplitud de $1/\sqrt{2}$ y una frecuencia normalizada de $\pi /2$ rad/muestra.

Calcule y represente el espectro de potencia de cada señal. Amplíe el rango de frecuencias de $0.15\pi$ rad/muestra a $0.6\pi$ rad/muestra. pspectrum escala el espectro de manera que, si el contenido de frecuencia de una señal cae exactamente dentro de un bin, su amplitud en ese bin es la potencia media verdadera de la señal. En una exponencial compleja, la potencia media es el cuadrado de la amplitud. Compruébelo calculando la transformada discreta de Fourier de la señal. Para obtener más detalles, consulte Measure Power of Deterministic Periodic Signals.

N = 128;
x = [1 1/sqrt(2)].*exp(1j*pi./[4;2]*(0:N-1)).';

[p,f] = pspectrum(x);

plot(f/pi,p)
hold on
stem(0:2/N:2-1/N,abs(fft(x)/N).^2)
hold off
axis([0.15 0.6 0 1.1])
legend("Channel "+[1;2]+", "+["pspectrum" "fft"])
grid

Genere una señal sinusoidal muestreada a 1 kHz durante 296 milisegundos e integrada en ruido blanco gaussiano. Especifique una frecuencia sinusoidal de 200 Hz y una varianza de ruido de 0,1². Almacene la señal y su información de tiempo en un horario de MATLAB®.

Fs = 1000;
t = (0:1/Fs:0.296)';
x = cos(2*pi*t*200)+0.1*randn(size(t));
xTable = timetable(seconds(t),x);

Calcule el espectro de potencia de la señal. Exprese el espectro en decibelios y represéntelo.

[pxx,f] = pspectrum(xTable);

plot(f,pow2db(pxx))
grid on
xlabel('Frequency (Hz)')
ylabel('Power Spectrum (dB)')
title('Default Frequency Resolution')

Vuelva a calcular el espectro de potencia de la sinusoide, pero esta vez utilice una resolución de frecuencia más gruesa de 25 Hz. Represente el espectro utilizando la función pspectrum sin argumentos de salida.

pspectrum(xTable,'FrequencyResolution',25)

Espectro bilateral

Genere una señal muestreada a 3 kHz durante 1 segundo. La señal es un chirp cuadrático convexo cuya frecuencia aumenta de 300 Hz a 1300 Hz durante la medición. El chirp está integrado en ruido blanco gaussiano.

fs = 3000;
t = 0:1/fs:1-1/fs;

x1 = chirp(t,300,t(end),1300,'quadratic',0,'convex') + ...
    randn(size(t))/100;

Calcule y represente el espectro de potencia bilateral de la señal con una ventana rectangular. En las señales reales, pspectrum representa un espectro unilateral de manera predeterminada. Para representar un espectro bilateral, establezca TwoSided como verdadero.

pspectrum(x1,fs,'Leakage',1,'TwoSided',true)

Genere una señal de valor complejo con la misma duración y tasa de muestreo. La señal es un chirp con contenido de frecuencia que varía sinusoidalmente y está integrada en ruido blanco. Calcule el espectrograma de la señal y muéstrelo como una gráfica de cascada. En las señales de valor complejo, el espectrograma es bilateral de forma predeterminada.

x2 = exp(2j*pi*100*cos(2*pi*2*t)) + randn(size(t))/100;

[p,f,t] = pspectrum(x2,fs,'spectrogram');

waterfall(f,t,p')
xlabel('Frequency (Hz)')
ylabel('Time (seconds)')
wtf = gca;
wtf.XDir = 'reverse';
view([30 45])

Manchado en las ventanas y resolución de tonos

Genere una señal de dos canales muestreada a 100 Hz durante 2 segundos.

1. El primer canal consta de un tono de 20 Hz y otro de 21 Hz. Ambos tonos tienen amplitud unitaria.

2. El segundo canal también tiene dos tonos. Un tono tiene amplitud unitaria y una frecuencia de 20 Hz. El otro tono tiene una amplitud de 1/100 y una frecuencia de 30 Hz.

fs = 100;
t = (0:1/fs:2-1/fs)';

x = sin(2*pi*[20 20].*t) + [1 1/100].*sin(2*pi*[21 30].*t);

Inserte la señal en ruido blanco. Especifique una relación señal-ruido de 40 dB. Represente las señales.

x = x + randn(size(x)).*std(x)/db2mag(40);

plot(t,x)

Calcule los espectros de los dos canales y muéstrelos.

pspectrum(x,t)

El valor predeterminado del manchado espectral, 0,5, corresponde a un ancho de banda de la resolución de aproximadamente 1,29 Hz. Los dos tonos del primer canal no se resuelven. El tono de 30 Hz en el segundo canal es visible, a pesar de ser mucho más débil que el otro.

Aumente el manchado a 0,85, lo que equivale a una resolución de unos 0,74 Hz. El tono débil del segundo canal es claramente visible.

pspectrum(x,t,'Leakage',0.85)

Aumente el manchado hasta el valor máximo. El ancho de banda de la resolución es aproximadamente 0,5 Hz. Los dos tonos del primer canal se resuelven. El tono débil del segundo canal queda enmascarado por los grandes lóbulos laterales de la ventana.

pspectrum(x,t,'Leakage',1)

Comparar las funciones spectrogram y pspectrum

Genere una señal que conste de un oscilador controlado por tensión y tres átomos gaussianos. La señal se muestrea a ${\mathit{f}}_{\mathit{s}}=2$ kHz durante 2 segundos.

fs = 2000;
tx = 0:1/fs:2;
gaussFun = @(A,x,mu,f) exp(-(x-mu).^2/(2*0.03^2)).*sin(2*pi*f.*x)*A';
s = gaussFun([1 1 1],tx',[0.1 0.65 1],[2 6 2]*100)*1.5;
x = vco(chirp(tx+.1,0,tx(end),3).*exp(-2*(tx-1).^2),[0.1 0.4]*fs,fs);
x = s+x';

Transformadas de Fourier de tiempo corto

Utilice la función pspectrum para calcular la STFT.

• Divida la señal de ${\mathit{N}}_{\mathit{x}}$ muestras en segmentos con longitud $\mathit{M}=80$ muestras, correspondientes a una resolución temporal de $80/2000=40$ milisegundos.

• Especifique $\mathit{L}=16$ muestras o el 20% de solapamiento entre los segmentos contiguos.

• Añada una ventana de Kaiser a cada segmento y especifique un manchado de $\ell =0.7$.

M = 80;
L = 16;
lk = 0.7;

[S,F,T] = pspectrum(x,fs,"spectrogram", ...
    TimeResolution=M/fs,OverlapPercent=L/M*100, ...
    Leakage=lk);

Compárela con el resultado obtenido con la función spectrogram.

• Especifique la longitud de la ventana y el solapamiento directamente en las muestras.

• pspectrum siempre usa una ventana de Kaiser como $\mathit{g}\left(\mathit{n}\right)$. El manchado $\ell$ y el factor de forma $\beta$ de la ventana están relacionados por $\beta =40\times \left(1-\ell \right)$.

• pspectrum siempre usa ${\mathit{N}}_{\mathrm{DFT}}=1024$ puntos cuando calcula la transformada discreta de Fourier. Puede especificar este número si desea calcular la transformada en un rango de frecuencias bilateral o centrado. Sin embargo, en las transformadas unilaterales, que son las predeterminadas para las señales reales, spectrogram utiliza $1024/2+1=513$ puntos. Como alternativa, puede especificar el vector de frecuencias en el que desea calcular la transformada, como en este ejemplo.

• Si una señal no puede dividirse exactamente en $\mathit{k}=\lfloor \frac{{\mathit{N}}_{\mathit{x}}-\mathit{L}}{\mathit{M}-\mathit{L}}\rfloor$ segmentos, spectrogram la trunca, mientras que pspectrum la rellena con ceros para crear un segmento extra. Para que las salidas sean equivalentes, elimine el segmento final y el elemento final del vector de tiempo.

• spectrogram devuelve la STFT, cuya magnitud elevada al cuadrado es el espectrograma. pspectrum devuelve el espectro de potencia segmento a segmento, que ya está elevado al cuadrado pero se divide por un factor de ${\sum }_{\mathit{n}}\mathit{g}\left(\mathit{n}\right)$ antes de elevarlo al cuadrado.

• En las transformadas unilaterales, pspectrum añade un factor extra de 2 al espectrograma.

g = kaiser(M,40*(1-lk));

k = (length(x)-L)/(M-L);
if k~=floor(k)
    S = S(:,1:floor(k));
    T = T(1:floor(k));
end

[s,f,t] = spectrogram(x/sum(g)*sqrt(2),g,L,F,fs);

Para mostrar los espectrogramas calculados por las dos funciones, utilice la función waterplot.

subplot(2,1,1)
waterplot(sqrt(S),F,T)
title("pspectrum")

subplot(2,1,2)
waterplot(s,f,t)
title("spectrogram")

maxd = max(max(abs(abs(s).^2-S)))

maxd = 
2.4419e-08

Espectros de potencia y gráficas de conveniencia

La función spectrogram tiene un cuarto argumento que se corresponde con el espectro de potencia segmento a segmento o con la densidad espectral de potencia. Al igual que la salida de pspectrum, el argumento ps ya está elevado al cuadrado e incluye el factor de normalización ${\sum }_{\mathit{n}}\mathit{g}\left(\mathit{n}\right)$. En los espectrogramas unilaterales de señales reales, hay que incluir el factor adicional de 2. Establezca el argumento de escala de la función en "power".

[~,~,~,ps] = spectrogram(x*sqrt(2),g,L,F,fs,"power");

max(abs(S(:)-ps(:)))

ans = 
2.4419e-08

Cuando se llaman sin argumentos de salida, tanto pspectrum como spectrogram representan el espectrograma de la señal en decibelios. Incluya el factor de 2 en los espectrogramas unilaterales. Establezca que los mapas de colores sean los mismos en ambas gráficas. Fije los límites del eje x en los mismos valores para hacer visible el segmento extra al final de la gráfica de pspectrum. En la gráfica de spectrogram, muestre la frecuencia en el eje y.

subplot(2,1,1)
pspectrum(x,fs,"spectrogram", ...
    TimeResolution=M/fs,OverlapPercent=L/M*100, ...
    Leakage=lk)
title("pspectrum")
cc = clim;
xl = xlim;

subplot(2,1,2)
spectrogram(x*sqrt(2),g,L,F,fs,"power","yaxis")
title("spectrogram")
clim(cc)
xlim(xl)

function waterplot(s,f,t)
% Waterfall plot of spectrogram
    waterfall(f,t,abs(s)'.^2)
    set(gca,XDir="reverse",View=[30 50])
    xlabel("Frequency (Hz)")
    ylabel("Time (s)")
end

Espectro de persistencia de una señal transitoria

Visualice una señal de interferencia de banda estrecha integrada en una señal de banda ancha.

Genere un chirp muestreado a 1 kHz durante 500 segundos. La frecuencia del chirp aumenta de 180 Hz a 220 Hz durante la medición.

fs = 1000;
t = (0:1/fs:500)';

x = chirp(t,180,t(end),220) + 0.15*randn(size(t));

La señal también contiene una sinusoide de 210 Hz. La sinusoide tiene una amplitud de 0,05 y está presente solo durante 1/6 de la duración total de la señal.

idx = floor(length(x)/6);
x(1:idx) = x(1:idx) + 0.05*cos(2*pi*t(1:idx)*210);

Calcule el espectrograma de la señal. Restrinja el rango de frecuencias de 100 Hz a 290 Hz. Especifique una resolución de tiempo de 1 segundo. Ambos componentes de la señal son visibles.

pspectrum(x,fs,'spectrogram', ...
    'FrequencyLimits',[100 290],'TimeResolution',1)

Calcule el espectro de potencia de la señal. La sinusoide débil queda oculta por el chirp.

pspectrum(x,fs,'FrequencyLimits',[100 290])

Calcule el espectro de persistencia de la señal. Ambos componentes de la señal son claramente visibles.

pspectrum(x,fs,'persistence', ...
    'FrequencyLimits',[100 290],'TimeResolution',1)

Espectrograma y espectrograma reasignado de chirp

Genere un chirp cuadrático muestreado a 1 kHz durante 2 segundos. El chirp tiene una frecuencia inicial de 100 Hz que aumenta hasta 200 Hz, en t = 1 segundo. Calcule el espectrograma con la configuración predeterminada de la función pspectrum. Use la función waterfall para representar el espectrograma.

fs = 1e3;
t = 0:1/fs:2;
y = chirp(t,100,1,200,"quadratic");

[sp,fp,tp] = pspectrum(y,fs,"spectrogram");

waterfall(fp,tp,sp')
set(gca,XDir="reverse",View=[60 60])
ylabel("Time (s)")
xlabel("Frequency (Hz)")

Calcule y muestre el espectrograma reasignado.

[sr,fr,tr] = pspectrum(y,fs,"spectrogram",Reassign=true);

waterfall(fr,tr,sr')
set(gca,XDir="reverse",View=[60 60])
ylabel("Time (s)")
xlabel("Frequency (Hz)")

Vuelva a calcular el espectrograma utilizando una resolución de tiempo de 0,2 segundos. Visualice el resultado con la función pspectrum sin argumentos de salida.

pspectrum(y,fs,"spectrogram",TimeResolution=0.2)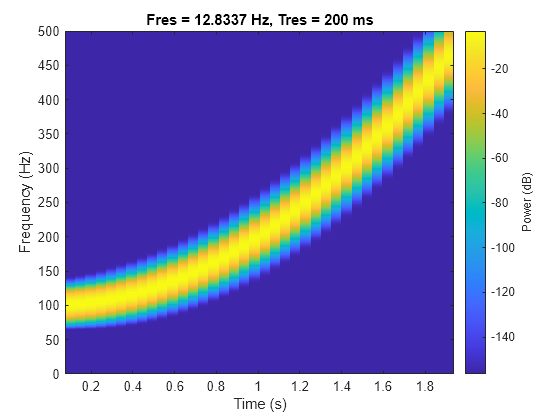

Calcule el espectrograma reasignado con la misma resolución de tiempo.

pspectrum(y,fs,"spectrogram",TimeResolution=0.2,Reassign=true)

Espectrograma de marcación por tonos

Cree una señal, muestreada a 4 kHz, que se asemeje a la pulsación de todas las teclas de un teléfono digital. Guarde la señal como un horario de MATLAB®.

fs = 4e3;
t = 0:1/fs:0.5-1/fs;

ver = [697 770 852 941];
hor = [1209 1336 1477];

tones = [];

for k = 1:length(ver)
    for l = 1:length(hor)
        tone = sum(sin(2*pi*[ver(k);hor(l)].*t))';
        tones = [tones;tone;zeros(size(tone))];
    end
end

% To hear, type soundsc(tones,fs)

S = timetable(seconds(0:length(tones)-1)'/fs,tones);

Calcule el espectrograma de la señal. Especifique una resolución de tiempo de 0,5 segundos y un solapamiento de cero entre los segmentos contiguos. Especifique que el manchado es de 0,85, lo que equivale aproximadamente a aplicar una ventana de Hann a los datos.

pspectrum(S,'spectrogram', ...
    'TimeResolution',0.5,'OverlapPercent',0,'Leakage',0.85)

El espectrograma muestra que cada tecla se pulsa durante medio segundo, con pausas silenciosas de medio segundo entre cada pulsación. El primer tono tiene un contenido de frecuencia concentrado en torno a 697 Hz y 1209 Hz, correspondiente al dígito '1' del sistema DTMF.

Argumentos de entrada

x — Señal de entrada

vector | matriz | horario

Señal de entrada, especificada como un vector, una matriz o un timetable de MATLAB^®.

• Si x es un horario, debe contener tiempos de fila finitos y crecientes.

  Nota

  Si en un horario faltan puntos de tiempo o están duplicados, puede solucionarlo con los consejos de Clean Timetable with Missing, Duplicate, or Nonuniform Times.

• Si x es un horario que representa una señal multicanal, debe tener una única variable que contenga una matriz o múltiples variables formadas por vectores.

Si x está muestreado de forma no uniforme, pspectrum interpola la señal a una malla uniforme para calcular las estimaciones espectrales. La función utiliza la interpolación lineal y asume un tiempo de muestreo igual a la mediana de las diferencias entre puntos de tiempo adyacentes. Para que una señal no muestreada uniformemente sea compatible, el intervalo de tiempo mediano y el intervalo de tiempo medio deben obedecer

$$\frac{1}{100}<\frac{\text{Median time interval}}{\text{Mean time interval}}<100.$$

Ejemplo: cos(pi./[4;2]*(0:159))'+randn(160,2) es una señal de dos canales formada por sinusoides integrada en ruido blanco.

Ejemplo: timetable(seconds(0:4)',rand(5,2)) especifica una variable aleatoria de dos canales muestreada a 1 Hz durante 4 segundos.

Ejemplo: timetable(seconds(0:4)',rand(5,1),rand(5,1)) especifica una variable aleatoria de dos canales muestreada a 1 Hz durante 4 segundos.

Tipos de datos: single | double
Soporte de números complejos: Sí

fs — Tasa de muestreo

2π (predeterminado) | escalar numérico positivo

Tasa de muestreo, especificada como un escalar numérico positivo.

t — Valores de tiempo

vector | arreglo datetime | arreglo duration | escalar duration

Valores de tiempo, especificados como un vector, un arreglo de datetime o duration, o un escalar de duration que representan el intervalo de tiempo entre las muestras.

Ejemplo: seconds(0:1/100:1) es un arreglo duration que representa 1 segundo de muestreo a 100 Hz.

Ejemplo: seconds(1) es un escalar duration que representa una diferencia de tiempo de 1 segundo entre muestras de señales consecutivas.

type — Tipo de espectro que calcular

'power' (predeterminado) | 'spectrogram' | 'persistence'

Tipo de espectro que calcular, especificado como 'power', 'spectrogram' o 'persistence':

• 'power': Calcula el espectro de potencia de la entrada. Utilice esta opción para analizar el contenido frecuencial de una señal estacionaria. Para obtener más información, consulte Cálculo del espectro.

• 'spectrogram': Calcula el espectrograma de la entrada. Utilice esta opción para analizar cómo cambia el contenido frecuencial de una señal a lo largo del tiempo. Para obtener más información, consulte Cálculo del espectrograma.

• 'persistence': Calcula el espectro de potencia de persistencia de la entrada. Utilice esta opción para visualizar la fracción de tiempo que un determinado componente de frecuencia está presente en una señal. Para obtener más información, consulte Cálculo del espectro de persistencia.

Nota

Las opciones 'spectrogram' y 'persistence' no son compatibles con la entrada multicanal.

Argumentos de par nombre-valor

Especifique pares de argumentos opcionales como Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value es el valor correspondiente. Los argumentos de nombre-valor deben aparecer después de otros argumentos. Sin embargo, el orden de los pares no importa.

En las versiones anteriores a la R2021a, utilice comas para separar cada nombre y valor, y encierre Name entre comillas.

Ejemplo: 'Leakage',1,'Reassign',true,'MinThreshold',-35 aplica una ventana rectangular a los datos, calcula una estimación del espectro reasignado y pone a cero todos los valores inferiores a -35 dB.

FrequencyLimits — Límites de la banda de frecuencia

[0 fs/2] (predeterminado) | vector numérico de dos elementos

Límites de la banda de frecuencia, especificados como el par separado por comas que consta de 'FrequencyLimits' y un vector numérico de dos elementos:

• Si la entrada contiene información temporal, la banda de frecuencia se expresa en Hz.

• Si la entrada no contiene información temporal, la banda de frecuencia se expresa en unidades normalizadas de rad/muestra.

De forma predeterminada, pspectrum calcula el espectro en todo el intervalo de Nyquist:

• Si la banda de frecuencia especificada contiene una región que cae fuera del intervalo de Nyquist, entonces pspectrum trunca la banda de frecuencia.

• Si la banda de frecuencia especificada se encuentra completamente fuera del intervalo de Nyquist, entonces pspectrum genera un error.

Consulte Cálculo del espectro para obtener más información sobre el intervalo de Nyquist.

Si x está muestreado de forma no uniforme, entonces pspectrum interpola linealmente la señal a una malla uniforme y define una tasa de muestreo efectiva igual a la inversa de la mediana de las diferencias entre puntos de tiempo adyacentes. Exprese 'FrequencyLimits' en términos de tasa de muestreo efectiva.

Ejemplo: [0.2*pi 0.7*pi] calcula el espectro entre 0.2π rad/muestra y 0.7π rad/muestra de una señal sin información de tiempo.

FrequencyResolution — Ancho de banda de la resolución de frecuencia

escalar numérico real

Ancho de banda de resolución de frecuencia, especificado como el par separado por comas que consta de 'FrequencyResolution' y un escalar numérico real, expresado en Hz si la entrada contiene información temporal, o en unidades normalizadas de rad/muestra en caso contrario. Este argumento no se puede especificar simultáneamente con 'TimeResolution'. El valor por defecto de este argumento depende del tamaño de los datos de entrada. Para obtener más detalles, consulte Cálculo del espectrograma.

Ejemplo: pi/100 calcula el espectro de una señal sin información de tiempo utilizando una resolución de frecuencia de π/100 rad/muestra.

Leakage — Manchado espectral

0.5 (predeterminado) | escalar numérico real entre 0 y 1

Manchado espectral, especificado como el par separado por comas que consta de 'Leakage' y un escalar numérico real entre 0 y 1. 'Leakage' controla la atenuación del lóbulo lateral de la ventana de Kaiser en relación con la anchura del lóbulo principal, manteniendo un equilibrio entre la mejora de la resolución y la disminución del manchado:

• Un valor de manchado grande resuelve los tonos muy espaciados, pero enmascara los tonos débiles cercanos.

• Un valor de manchado pequeño encuentra tonos pequeños en la proximidad de tonos más grandes, pero difumina las frecuencias cercanas.

Ejemplo: 'Leakage',0 reduce los manchados al mínimo a costa de la resolución espectral.

Ejemplo: 'Leakage',0.85 aplica una ventana de Hann a los datos.

Ejemplo: 'Leakage',1 equivale a aplicar una ventana rectangular a los datos, maximizando el manchado pero mejorando la resolución espectral.

MinThreshold — Límite inferior para valores distintos de cero

-Inf (predeterminado) | escalar real

Límite inferior para valores distintos de cero, especificado como el par separado por comas que consta de 'MinThreshold' y un escalar real. pspectrum implementa 'MinThreshold' de forma diferente según el valor del argumento type:

• 'power' o 'spectrogram': pspectrum establece como cero aquellos elementos de p que cumplen 10 log₁₀(p) ≤ 'MinThreshold'. Especifique 'MinThreshold' en decibelios.

• 'persistence': pspectrum establece como cero aquellos elementos de p que son inferiores a 'MinThreshold'. Especifique 'MinThreshold' entre 0 y 100%.

NumPowerBins — Número de bins de potencia para el espectro de persistencia

256 (predeterminado) | entero entre 20 y 1024

Número de bins de potencia para el espectro de persistencia, especificado como el par separado por comas que consta de 'NumPowerBins' y un entero entre 20 y 1024.

OverlapPercent — Solapamiento entre segmentos contiguos

escalar real en el intervalo [0, 100)

Solapamiento entre segmentos contiguos para el espectrograma o el espectro de persistencia, especificado como el par separado por comas que consta de 'OverlapPercent' y un escalar real en el intervalo [0, 100). El valor predeterminado de este argumento depende de la ventana espectral. Para obtener más detalles, consulte Cálculo del espectrograma.

Reassign — Opción de reasignación

false (predeterminado) | true

Opción de reasignación, especificada como el par separado por comas que consta de 'Reassign' y un valor lógico. Si esta opción se establece como true, entonces pspectrum agudiza la localización de las estimaciones espectrales realizando una reasignación de tiempo y frecuencia. La técnica de reasignación produce periodogramas y espectrogramas más fáciles de leer e interpretar. Esta técnica reasigna cada estimación espectral al centro de energía de su bin, en lugar del centro geométrico de este. La técnica proporciona una localización exacta de los chirps e impulsos.

TimeResolution — Resolución de tiempo del espectrograma o del espectro de persistencia

escalar real

Resolución temporal del espectrograma o del espectro de persistencia, especificada como el par separado por comas que consta de 'TimeResolution' y un escalar real, expresado en segundos si la entrada contiene información temporal, o como un número entero de muestras en caso contrario. Este argumento controla la duración de los segmentos utilizados para calcular los espectros de potencia de tiempo corto que forman las estimaciones del espectrograma o del espectro de persistencia. 'TimeResolution' no puede especificarse simultáneamente con 'FrequencyResolution'. El valor predeterminado de este argumento depende del tamaño de los datos de entrada y, si se ha especificado, de la resolución de la frecuencia. Para obtener más detalles, consulte Cálculo del espectrograma.

TwoSided — Estimación espectral bilateral

falso | verdadero

Estimación espectral bilateral, especificada como el par separado por comas que consta de 'TwoSided' y un valor lógico.

• Si esta opción es true, la función calcula estimaciones de espectro centradas y bilaterales sobre [–π, π]. Si la entrada tiene información temporal, las estimaciones se calculan sobre [–f_s/2, f_s/2], donde f_s es la tasa de muestreo efectiva.

• Si la opción es false, la función calcula estimaciones de espectro unilaterales sobre el intervalo de Nyquist [0, π]. Si la entrada tiene información temporal, las estimaciones se calculan sobre [0, f_s/2], donde f_s es la tasa de muestreo efectiva. Para conservar la potencia total, la función multiplica la potencia por 2 en todas las frecuencias excepto 0 y la frecuencia de Nyquist. Esta opción es válida solo para señales reales.

Si no se especifica, 'TwoSided' es por defecto false en señales de entrada reales y true en señales de entrada complejas.

Argumentos de salida

p — Espectro

vector | matriz

Espectro, devuelto como un vector o una matriz. El tipo y el tamaño del espectro dependen del valor del argumento type:

• 'power': p contiene la estimación del espectro de potencia de cada canal de x. En este caso, p es del tamaño N_r × N_ch, donde N_f es la longitud de f y N_ch es el número de canales de x. pspectrum escala el espectro de manera que, si el contenido de frecuencia de una señal cae exactamente dentro de un bin, su amplitud en ese bin es la potencia media verdadera de la señal. Por ejemplo, la potencia media de una sinusoide es la mitad del cuadrado de la amplitud de la sinusoide. Para obtener más detalles, consulte Measure Power of Deterministic Periodic Signals.

• 'spectrogram': p contiene una estimación del espectro de potencia en tiempo corto y localizado en el tiempo de x. En este caso, p es del tamaño N_f × N_t, donde N_f es la longitud de f y N_t es la longitud de t.

• 'persistence': p contiene las probabilidades, expresadas en porcentajes, de que la señal tenga componentes de un determinado nivel de potencia en una ubicación de tiempo y frecuencia determinada. En este caso, p es del tamaño N_pwr × N_f, donde N_pwr es la longitud de pwr y N_f es la longitud de f.

f — Frecuencias del espectro

vector

Frecuencias del espectro, devueltas como vector. Si la señal de entrada contiene información temporal, f contiene frecuencias expresadas en Hz. Si la señal de entrada no contiene información de tiempo, las frecuencias están en unidades normalizadas de rad/muestra.

t — Valores de tiempo del espectrograma

vector | arreglo datetime | arreglo duration

Valores de tiempo del espectrograma, devueltos como vector de valores de tiempo en segundos o como arreglo de duration. Si la entrada no tiene información de tiempo, entonces t contiene números de muestra. t contiene los valores de tiempo correspondientes a los centros de los segmentos de datos utilizados para calcular las estimaciones del espectro de potencia en tiempo corto.

• Si la entrada de pspectrum es un horario, entonces t tiene el mismo formato que los valores de tiempo del horario de entrada.

• Si la entrada de pspectrum es un vector numérico muestreado en un conjunto de instantes de tiempo especificado por una matriz numérica, duration, o el arreglo datetime, entonces t tiene el mismo tipo y formato que los valores de tiempo de entrada.

• Si la entrada de pspectrum es un vector numérico con una diferencia de tiempo especificada entre muestras consecutivas, entonces t es un arreglo de duration.

pwr — Valores de potencia del espectro de persistencia

vector

Valores de potencia del espectro de persistencia, devueltos como vector.

Más acerca de

Cálculo del espectro

Para calcular el espectro de la señal, pspectrum encuentra un compromiso entre la resolución espectral alcanzable con toda la longitud de la señal y las limitaciones de rendimiento que se derivan del cálculo de grandes FFT:

• Si es posible, la función calcula un único periodograma modificado de toda la señal utilizando una ventana de Kaiser.

• Si no es posible calcular un solo periodograma modificado en un tiempo razonable, la función calcula un periodograma de Welch: Este divide la señal en segmentos superpuestos, les aplica una ventana de Kaiser y calcula el promedio de los periodogramas de los segmentos.

Ventaneo espectral

Cualquier señal del mundo real solo se puede medir durante un período de tiempo finito. Este hecho introduce efectos no desdeñables en el análisis de Fourier, que supone que las señales son periódicas o infinitamente largas. El uso de ventaneo espectral, que asigna diferentes ponderaciones a las distintas muestras de señales, se ocupa sistemáticamente de los efectos de tamaño finito.

La forma más sencilla de aplicar una ventana a una señal es suponer que es idéntica a cero fuera del intervalo de medición y que todas las muestras son igualmente significativas. Esta "ventana rectangular" tiene saltos discontinuos en ambos extremos que dan lugar a anillos espectrales. Todas las demás ventanas espectrales se estrechan en ambos extremos para atenuar este efecto asignando ponderaciones menores a las muestras cercanas a los bordes de la señal.

El proceso de ventaneo siempre implica un compromiso entre objetivos contradictorios, que son la mejora de la resolución y la disminución de los manchados:

• La resolución es la capacidad de conocer con precisión cómo se distribuye la energía de la señal en el espacio de la frecuencia. Un analizador de espectros con una resolución ideal puede distinguir dos tonos diferentes (sinusoides puras) presentes en la señal, por muy cercanos que estén en frecuencia. Cuantitativamente, esta capacidad se relaciona con la anchura del lóbulo principal de la transformada de la ventana.

• El manchado es el hecho de que, en una señal finita, cada componente de frecuencia proyecta un contenido de energía en todo el intervalo de frecuencias. La cantidad de manchado en un espectro puede medirse por la capacidad de detectar un tono débil entre el ruido en presencia de un tono contiguo fuerte. Cuantitativamente, esta capacidad se relaciona con el nivel de lóbulos laterales de la transformada de frecuencia de la ventana.

• El espectro se normaliza para que un tono puro dentro de ese ancho de banda, si está perfectamente centrado, tenga la amplitud correcta.

Cuanto mejor sea la resolución, mayor será el manchado, y viceversa. En un extremo del intervalo, una ventana rectangular tiene el lóbulo principal más estrecho posible y los lóbulos laterales más altos. Esta ventana puede resolver tonos muy espaciados si tienen un contenido energético similar, pero no encuentra el más débil en caso contrario. En el otro extremo, una ventana con alta supresión de lóbulos laterales tiene un lóbulo principal amplio en el que las frecuencias cercanas se mezclan.

pspectrum utiliza ventanas de Kaiser para llevar a cabo el proceso de ventaneo. En las ventanas Kaiser, la fracción de la energía de la señal captada por el lóbulo principal depende sobre todo de un factor de forma ajustable, β. pspectrum utiliza factores de forma que van desde β = 0, que se corresponde con una ventana rectangular, hasta β = 40, donde un lóbulo principal amplio captura esencialmente toda la energía espectral representable en doble precisión. Un valor intermedio de β ≈ 6 se aproxima bastante a una ventana de Hann. Para controlar β, utilice el par nombre-valor 'Leakage'. Si establece 'Leakage' en ℓ, entonces ℓ y β están relacionados por β = 40(1 – ℓ). Para obtener más detalles, consulte kaiser.

Ventana de Hann de 51 puntos y ventana de Kaiser de 51 puntos con β = 5.7 en el dominio de tiempo	Ventana de Hann de 51 puntos y ventana de Kaiser de 51 puntos con β = 5.7 en el dominio de frecuencia

Selección de parámetros y algoritmos

Para calcular los espectros de la señal, pspectrum determina inicialmente el ancho de banda de resolución, que mide lo cerca que pueden estar dos tonos y seguir resolviéndose. El ancho de banda de resolución tiene un valor teórico de

$${\text{RBW}}_{\text{theory}}=\frac{\text{ENBW}}{t_{\max }-t_{\min }}.$$

• t_max – t_min, la longitud de registro, es la duración en el dominio de tiempo de la región de la señal seleccionada.

• ENBW es el ancho de banda de ruido equivalente de la ventana espectral. Para obtener más detalles, consulte enbw.

  Controle el ENBW con el par nombre-valor 'Leakage'. El valor mínimo del argumento se corresponde con una ventana de Kaiser con β = 40. El valor máximo se corresponde con una ventana de Kaiser con β = 0.

Sin embargo, en la práctica, pspectrum podría bajar la resolución. Al bajar la resolución se puede calcular el espectro en un tiempo razonable y mostrarlo con un número finito de píxeles. Por estas razones prácticas, el menor ancho de banda de resolución que puede utilizar pspectrum es

$${\text{RBW}}_{\text{performance}}=\frac{f_{\text{span}}}{4096-1},$$

, donde f_span es la anchura de la banda de frecuencia especificada mediante 'FrequencyLimits'. Si no se especifica 'FrequencyLimits', pspectrum usa la tasa de muestreo como f_span. RBW_performance no se puede ajustar.

Para calcular el espectro de una señal, la función elige el mayor de los dos valores, denominado ancho de banda de resolución objetivo:

$$\text{RBW}=\max ({\text{RBW}}_{\text{theory}},{\text{RBW}}_{\text{performance}}).$$

• Si el ancho de banda de resolución es RBW_theory, pspectrum calcula un único periodograma modificado en toda la señal. La función utiliza una ventana de Kaiser con un factor de forma controlado por el par nombre-valor 'Leakage'. Para obtener más detalles, consulte periodogram.

• Si el ancho de banda de resolución es RBW_performance, pspectrum calcula un periodograma de Welch para la señal. La función:

  1. Divide las señales en segmentos superpuestos.

  2. Aplica una ventana a cada segmento por separado utilizando una ventana Kaiser con el factor de forma especificado.

  3. Calcula el promedio de los periodogramas de todos los segmentos.

  El procedimiento de Welch está diseñado para reducir la varianza de la estimación del espectro calculando el promedio de diferentes "realizaciones" de las señales, dadas por las secciones superpuestas, y utilizando la ventana para eliminar los datos redundantes. Para obtener más detalles, consulte pwelch.

  • La longitud de cada segmento (o, de forma equivalente, de la ventana) se calcula utilizando

    $$\text{Segment length}=\frac{f_{\text{Nyquist}}\times \text{ENBW}}{\text{RBW}},$$

    donde f_Nyquist es la frecuencia de Nyquist. (Si no hay solapamiento, la frecuencia de Nyquist es la mitad de la tasa de muestreo efectiva, definida como la inversa de la mediana de las diferencias entre puntos temporales adyacentes. El intervalo Nyquist es [0, f_Nyquist] para señales reales y [–f_Nyquist, f_Nyquist] para señales complejas.)

  • La longitud de paso se encuentra ajustando una estimación inicial,

    $$\text{Stride length}=\frac{\text{Window length}}{2\times \text{ENBW}-1},$$

    para que la primera ventana empiece exactamente en la primera muestra del primer segmento y la última ventana termine exactamente en la última muestra del último segmento.

Cálculo del espectrograma

Para calcular el espectro dependiente del tiempo de una señal no estacionaria, pspectrum divide la señal en segmentos superpuestos, les aplica una ventana de Kaiser, calcula la transformada de Fourier en tiempo corto y luego concatena las transformadas para formar una matriz. Para obtener más información, consulte Cálculo de espectrogramas con Signal Processing Toolbox.

Una señal no estacionaria es una señal cuyo contenido de frecuencia cambia con el tiempo. El espectrograma de una señal no estacionaria es una estimación de la evolución temporal de su contenido frecuencial. Para crear el espectrograma de una señal no estacionaria, pspectrum sigue estos pasos:

1. Divide la señal en segmentos de igual longitud. Los segmentos deben ser lo suficientemente cortos como para que el contenido de frecuencia de la señal no cambie de forma apreciable dentro de un segmento. Los segmentos pueden solaparse o no.

2. Aplica una ventana a cada segmento y calcula su espectro para obtener la transformada de Fourier de tiempo corto.

3. Utiliza los espectros de los segmentos para construir el espectrograma:

   • Si se llama con argumentos de salida, concatena los espectros para formar una matriz.

   • Si se llama sin argumentos de salida, muestra la potencia de cada espectro en decibelios segmento por segmento. Representa las magnitudes una al lado de la otra como una imagen con un mapa de colores que depende de la magnitud.

La función puede calcular el espectrograma solo en señales de un solo canal.

División de la señal en segmentos

Para construir un espectrograma, primero hay que dividir la señal en segmentos posiblemente superpuestos. Con la función pspectrum se puede controlar la longitud de los segmentos y la cantidad de solapamiento entre segmentos contiguos mediante los argumentos de par nombre-valor 'TimeResolution' y 'OverlapPercent'. Si no se especifica la longitud y el solapamiento, la función elige una longitud basada en la longitud total de la señal y un porcentaje de solapamiento dado por

$$\left(1-\frac{\text{1}}{2\times \text{ENBW}-1}\right)\times 100,$$

, donde ENBW es el ancho de banda de ruido equivalente de la ventana espectral. Para obtener más información, consulte enbw y Cálculo del espectro.

Resolución de tiempo especificada

• Si la señal no tiene información de tiempo, especifique la resolución de tiempo (longitud de segmento) en muestras. La resolución de tiempo debe ser un entero mayor o igual a 1 y menor o igual a la longitud de la señal.

  Si la señal tiene información de tiempo, especifique la resolución de tiempo en segundos. La función convierte el resultado en un número de muestras y lo redondea al entero más cercano que sea menor o igual que el número pero no menor que 1. La resolución de tiempo debe ser menor o igual a la duración de la señal.

• Especifique el solapamiento como un porcentaje de la longitud del segmento. La función convierte el resultado en un número de muestras y lo redondea al entero más cercano que sea menor o igual que el número.

Resolución de tiempo predeterminada

Si no se especifica una resolución de tiempo, entonces pspectrum utiliza la longitud de la señal completa para elegir la longitud de los segmentos. La función establece la resolución de tiempo como ⌈N/d⌉ muestras, donde los símbolos ⌈⌉ denotan la función de techo, N es la longitud de la señal, y d es un divisor que depende de N:

Longitud de la señal (N)	Divisor (d)	Longitud del segmento
2 muestras– 63 muestras	2	1 muestra– 32 muestras
64 muestras– 255 muestras	8	8 muestras– 32 muestras
256 muestras– 2047 muestras	8	32 muestras– 256 muestras
2048 muestras– 4095 muestras	16	128 muestras– 256 muestras
4096 muestras– 8191 muestras	32	128 muestras– 256 muestras
8192 muestras– 16383 muestras	64	128 muestras– 256 muestras
16384 muestras– N muestras	128	128 muestras– ⌈ N / 128 ⌉ muestras

Todavía se puede especificar el solapamiento entre segmentos contiguos. Al especificar el solapamiento se modifica el número de segmentos. Los segmentos que se extienden más allá del punto final de la señal se rellenan con ceros.

Considere la señal de siete muestras [s0 s1 s2 s3 s4 s5 s6]. Como ⌈7/2⌉ = ⌈3.5⌉ = 4, la función divide la señal en dos segmentos de longitud cuatro cuando no hay solapamiento. El número de segmentos cambia a medida que aumenta el solapamiento.

Número de muestras solapadas	Segmentos resultantes
0	s0 s1 s2 s3 s4 s5 s6 0
1	s0 s1 s2 s3 s3 s4 s5 s6
2	s0 s1 s2 s3 s2 s3 s4 s5 s4 s5 s6 0
3	s0 s1 s2 s3 s1 s2 s3 s4 s2 s3 s4 s5 s3 s4 s5 s6

pspectrum rellena con ceros la señal si el último segmento se extiende más allá del punto final. La función devuelve t, un vector de instantes de tiempo que se corresponde con los centros de los segmentos.

Aplicación de ventanas a los segmentos y cálculo de los espectros

Después de que pspectrum divida la señal en segmentos superpuestos, la función les aplica una ventana de Kaiser a cada uno. El factor de forma β de la ventana, y por tanto el manchado, puede ajustarse mediante el par nombre-valor 'Leakage'. A continuación, la función calcula el espectro de cada segmento y concatena los espectros para formar la matriz del espectrograma. Para calcular los espectros de los segmentos, pspectrum sigue el procedimiento descrito en Cálculo del espectro, salvo que el límite inferior del ancho de banda de resolución sea

$${\text{RBW}}_{\text{performance}}=4\times \frac{f_{\text{span}}}{1024-1}.$$

Mostrar la potencia del espectro

Si se llama sin argumentos de salida, la función muestra la potencia de la transformada de Fourier de tiempo corto en decibelios, utilizando una barra de color con el mapa de colores predeterminado de MATLAB. La barra de color comprende todo el intervalo de potencia del espectrograma.

Cálculo del espectro de persistencia

El espectro de persistencia es una vista de tiempo-frecuencia que muestra el porcentaje del tiempo que está presente una frecuencia concreta en una señal. El espectro de persistencia es un histograma en el espacio potencia-frecuencia. Cuanto más tiempo persiste una frecuencia concreta en una señal a medida que la señal evoluciona, mayor es el porcentaje de tiempo y, por lo tanto, más brillante o "cálido" el color en la visualización. Utilice el espectro de persistencia para identificar señales ocultas en otras señales.

pspectrum sigue estos pasos para calcular el espectro de persistencia:

1. Calcula el espectrograma utilizando el manchado, la resolución temporal y el solapamiento especificados. Para obtener más detalles, consulte Cálculo del espectrograma.

2. Partición de los valores de potencia y de frecuencia en bins bidimensionales. (Para especificar el número de bins de potencia, utilice el par nombre-valor 'NumPowerBins'.)

3. Para cada valor de tiempo, calcula un histograma bivariado del logaritmo del espectro de potencia. Para cada bin de potencia-frecuencia en el que haya energía de la señal en ese instante, aumenta en 1 el elemento de la matriz correspondiente. Suma los histogramas de todos los valores de tiempo.

4. Representa el histograma acumulado frente a la potencia y la frecuencia, con el color proporcional al logaritmo de los recuentos del histograma expresado en porcentajes normalizados. Para representar valores cero, utilice la mitad de la menor magnitud posible.

Espectro de potencia

Histogramas

Histograma acumulado

Referencias

[1] harris, fredric j. “On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform.” Proceedings of the IEEE^®. Vol. 66, January 1978, pp. 51–83.

[2] Welch, Peter D. "The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms." IEEE Transactions on Audio and Electroacoustics. Vol. 15, June 1967, pp. 70–73.

Capacidades ampliadas

Generación de código C/C++
Genere código C y C++ mediante MATLAB® Coder™.

Arreglos GPU

Acelere código mediante la ejecución en una unidad de procesamiento gráfico (GPU) mediante Parallel Computing Toolbox™.

La función pspectrum es compatible con entradas de arreglos de GPU con estas notas y limitaciones de uso:

• No se admite el espectro de persistencia.

• No se admite el espectrograma o el espectro reasignado.

Para obtener más información, consulte Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Historial de versiones

Introducido en R2017b

R2023b: Utilizar horarios para la generación de código

La función pspectrum admite horarios de MATLAB para la generación de código.

R2023a: Visualizar salidas de funciones empleando la tarea de Live Editor Create Plot

Ahora puede usar la tarea de Live Editor Create Plot para visualizar la salida de pspectrum de forma interactiva. Puede seleccionar diferentes tipos de gráficas y establecer parámetros opcionales. La tarea también genera automáticamente código que se convierte en parte de su script en vivo.

Consulte también

Apps

• Signal Analyzer

Funciones

• periodogram | pwelch | spectrogram | stft

Temas

• Cálculo de espectrogramas con Signal Processing Toolbox
• Time-Frequency Gallery
• Practical Introduction to Time-Frequency Analysis

Teaching Resources

• Procesamiento digital de señales: Diseño de filtros y señales (Recursos didácticos de MathWorks)