Respuesta en frecuencia
Dominio digital
freqz utiliza un algoritmo basado en FFT para calcular la respuesta en frecuencia de la transformada Z de un filtro digital. Específicamente, la instrucción
[h,w] = freqz(b,a,p)
devuelve la respuesta en frecuencia compleja de p puntos, H(ejω), del filtro digital.
En su forma más sencilla, freqz acepta los vectores de coeficiente de filtro b y a, así como un entero p que especifique el número de puntos en los que calcular la respuesta en frecuencia. freqz devuelve la respuesta en frecuencia compleja en el vector h y los puntos reales de frecuencia en el vector w en rad/s.
freqz puede aceptar otros parámetros, como la frecuencia de muestreo o un vector de puntos de frecuencia arbitrarios. El siguiente ejemplo encuentra la respuesta en frecuencia de 256 puntos para un filtro Chebyshev de tipo I de 12.º orden. Llamar a freqz especifica una frecuencia de muestreo fs de 1000 Hz:
[b,a] = cheby1(12,0.5,200/500); [h,f] = freqz(b,a,256,1000);
Puesto que la lista de parámetros incluye una frecuencia de muestreo, freqz devuelve un vector f que contiene los 256 puntos de frecuencia entre 0 y fs/2 utilizados en el cálculo de la respuesta en frecuencia.
Nota
Esta toolbox utiliza la convención de que la unidad de frecuencia es la frecuencia de Nyquist, definida como la mitad de la frecuencia de muestreo. La frecuencia de Nyquist normaliza el parámetro de frecuencia de corte para todas las funciones básicas de diseño de filtros. Para un sistema con una frecuencia de muestreo de 1000 Hz, por ejemplo, 300 Hz es 300/500 = 0,6. Para convertir la frecuencia normalizada en frecuencia angular en torno al círculo de la unidad, multiplique por π. Para volver a convertir la frecuencia normalizada en hercios, multiplique por la mitad de la frecuencia de muestreo.
Si llama a freqz sin argumentos de salida, representa tanto la magnitud en lugar de la frecuencia como la fase en lugar de la frecuencia. Por ejemplo, un filtro Butterworth de paso bajo de noveno orden con una frecuencia de corte de 400 Hz, basado en una frecuencia de muestreo de 2000 Hz, es
[b,a] = butter(9,400/1000);
Para calcular la respuesta en frecuencia compleja de 256 puntos para este filtro y representar la magnitud y la fase con freqz, utilice
freqz(b,a,256,2000)
freqz también puede aceptar un vector de puntos de frecuencia arbitrarios para utilizarlo en el cálculo de la respuesta en frecuencia. Por ejemplo,
w = linspace(0,pi); h = freqz(b,a,w);
calcula la respuesta en frecuencia compleja en los puntos de frecuencia en w para el filtro definido por los vectores b y a. Los puntos de frecuencia pueden ir desde 0 a 2π. Para especificar un vector de frecuencia que vaya desde cero a su frecuencia de muestreo, incluya tanto el vector de frecuencia como el valor de frecuencia de muestreo en la lista de parámetros.
Estos ejemplos muestran cómo calcular y mostrar las respuestas en frecuencia digitales.
Respuesta de frecuencia de la función de transferencia
Calcule y muestre la respuesta de magnitud del filtro paso bajo IIR de tercer orden descrito por la siguiente función de transferencia:
Exprese el numerador y el denominador como convoluciones de polinomios. Encuentre la respuesta de frecuencia en 2001 puntos que abarcan todo el círculo de la unidad.
b0 = 0.05634;
b1 = [1 1];
b2 = [1 -1.0166 1];
a1 = [1 -0.683];
a2 = [1 -1.4461 0.7957];
b = b0*conv(b1,b2);
a = conv(a1,a2);
[h,w] = freqz(b,a,'whole',2001);Represente la respuesta de magnitud expresada en decibelios.
plot(w/pi,20*log10(abs(h))) ax = gca; ax.YLim = [-100 20]; ax.XTick = 0:.5:2; xlabel('Normalized Frequency (\times\pi rad/sample)') ylabel('Magnitude (dB)')

Respuesta de frecuencia de un filtro paso banda FIR
Diseñe un filtro paso banda FIR con una banda de paso entre y rad/muestra y 3 dB de ondulación. La primera banda de parada va de a rad/muestra y tiene una atenuación de 40 dB. La segunda banda de parada va de rad/muestra a la frecuencia de Nyquist y tiene una atenuación de 30 dB. Calcule el valor de la frecuencia de respuesta. Represente su magnitud tanto en unidades lineales como en decibelios. Resalte la banda de paso.
sf1 = 0.1; pf1 = 0.35; pf2 = 0.8; sf2 = 0.9; pb = linspace(pf1,pf2,1e3)*pi; bp = designfilt("bandpassfir", ... StopbandAttenuation1=40,StopbandFrequency1=sf1, ... PassbandFrequency1=pf1,PassbandRipple=3, ... PassbandFrequency2=pf2,StopbandFrequency2=sf2, ... StopbandAttenuation2=30); [h,w] = freqz(bp,1024); hpb = freqz(bp,pb); subplot(2,1,1) plot(w/pi,abs(h),pb/pi,abs(hpb),'.-') axis([0 1 -1 2]) legend("Response","Passband",Location="south") ylabel("Magnitude") subplot(2,1,2) plot(w/pi,db(h),pb/pi,db(hpb),".-") axis([0 1 -60 10]) xlabel("Normalized Frequency (\times\pi rad/sample)") ylabel("Magnitude (dB)")

Respuesta de magnitud de un filtro de paso alto
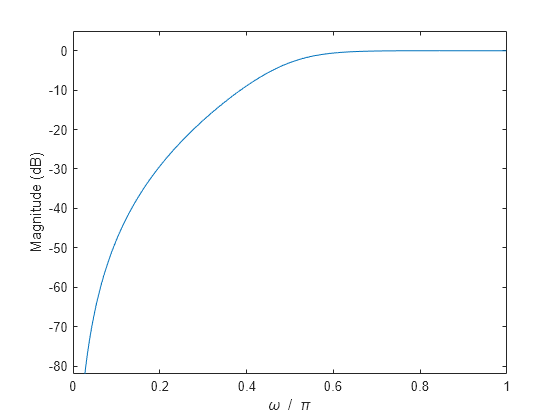
Diseñe un filtro Butterworth de paso alto de tercer orden que tenga una frecuencia 3 dB normalizada de rad/muestra. Calcule su respuesta en frecuencia. Exprese la respuesta de magnitud en decibelios y represéntela.
[b,a] = butter(3,0.5,'high'); [h,w] = freqz(b,a); dB = mag2db(abs(h)); plot(w/pi,dB) xlabel('\omega / \pi') ylabel('Magnitude (dB)') ylim([-82 5])
Dominio analógico
freqs evalúa la respuesta en frecuencia para un filtro analógico definido por dos vectores de coeficiente de entrada: b y a. Su operación es similar a la de freqz; puede especificar un número de puntos de frecuencia que utilizar, suministrar un vector de puntos de frecuencia arbitrarios y representar la respuesta de magnitud y de fase del filtro. Este ejemplo muestra cómo calcular y mostrar las respuestas en frecuencia analógicas.
Comparación de filtros paso bajo IIR analógicos
Diseñe un filtro analógico Butterworth paso bajo de quinto orden con una frecuencia de corte de 2 GHz. Multiplique por para convertir la frecuencia en radianes por segundo. Calcule la respuesta en frecuencia del filtro en 4096 puntos.
n = 5;
wc = 2*pi*2e9;
w = 2*pi*1e9*logspace(-2,1,4096)';
[zb,pb,kb] = butter(n,wc,"s");
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,w);
gdb = -diff(unwrap(angle(hb)))./diff(wb);Diseñe un filtro Chebyshev tipo I de quinto orden con la misma frecuencia de borde y 3 dB de ondulación de la banda de paso. Calcule su respuesta en frecuencia.
[z1,p1,k1] = cheby1(n,3,wc,"s");
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,w);
gd1 = -diff(unwrap(angle(h1)))./diff(w1);Diseñe un filtro Chebyshev tipo II de quinto orden con la misma frecuencia de borde y 30 dB de atenuación de la banda de parada. Calcule su respuesta en frecuencia.
[z2,p2,k2] = cheby2(n,30,wc,"s");
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,w);
gd2 = -diff(unwrap(angle(h2)))./diff(w2);Diseñe un filtro elíptico de quinto orden con la misma frecuencia de borde, 3 dB de ondulación de la banda de paso y 30 dB de atenuación de la banda de parada. Calcule su respuesta en frecuencia.
[ze,pe,ke] = ellip(n,3,30,wc,"s");
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,w);
gde = -diff(unwrap(angle(he)))./diff(we);Diseñe un filtro de Bessel de quinto orden con la misma frecuencia de borde. Calcule su respuesta en frecuencia.
[zf,pf,kf] = besself(n,wc); [bf,af] = zp2tf(zf,pf,kf); [hf,wf] = freqs(bf,af,w); gdf = -diff(unwrap(angle(hf)))./diff(wf);
Represente la atenuación en decibelios. Exprese la frecuencia en gigahercios. Compare los filtros.
fGHz = [wb w1 w2 we wf]/(2e9*pi); plot(fGHz,mag2db(abs([hb h1 h2 he hf]))) axis([0 5 -45 5]) grid on xlabel("Frequency (GHz)") ylabel("Attenuation (dB)") legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Represente el retardo de grupo en las muestras. Exprese la frecuencia en gigahercios y el retardo de grupo en nanosegundos. Compare los filtros.
gdns = [gdb gd1 gd2 gde gdf]*1e9; gdns(gdns<0) = NaN; loglog(fGHz(2:end,:),gdns) grid on xlabel("Frequency (GHz)") ylabel("Group delay (ns)") legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Los filtros Butterworth y Chebyshev Tipo II tienen bandas de paso planas y bandas de transición anchas. Los filtros Chebyshev de tipo I y elíptico se desinflan más rápido pero tienen ondulaciones en la banda de paso. La entrada de frecuencia a la función de diseño Chebyshev Tipo II establece el comienzo de la banda de parada en lugar del final de la banda de paso. El filtro de Bessel tiene un retardo de grupo aproximadamente constante a lo largo de la banda de paso.