Suavizar señales
Este ejemplo muestra cómo utilizar filtros de media móvil y el remuestreo para aislar el efecto de componentes periódicos del momento del día sobre las lecturas de temperatura por hora, y también cómo eliminar ruido no deseado de un cable en una medición de voltaje de lazo abierto. Este ejemplo también muestra cómo suavizar los niveles de una señal horaria al tiempo que se preservan los bordes utilizando un filtro de mediana. El ejemplo también muestra cómo utilizar un filtro de Hampel para eliminar valores atípicos grandes.
Motivo
El suavizado nos permite descubrir patrones importantes en nuestros datos mientras omitimos elementos que no son importantes (por ejemplo, ruido). Utilizamos el filtrado para realizar este suavizado. El objetivo del suavizado es producir cambios lentos en el valor para que resulte más sencillo ver tendencias en nuestros datos.
A veces, cuando se examinan datos de entrada, es posible que queramos suavizarlos para ver una tendencia en la señal. En nuestro ejemplo, tenemos un conjunto de lecturas de temperatura en grados Celsius tomadas cada hora en el Aeropuerto Logan de Boston durante todo el mes de enero de 2011.
load bostemp days = (1:31*24)/24; plot(days, tempC) axis tight ylabel("Temperature (\circC)") xlabel("Time elapsed from Jan 1, 2011 (days)") title("Logan Airport Dry Bulb Temperature (source: NOAA)")

Observe que podemos ver el efecto que el momento del día tiene sobre las lecturas de temperatura. Si solo le interesa la variación diaria de temperatura a lo largo del mes, las fluctuaciones horarias solo aportan ruido, lo que dificultaría la posibilidad de discernir las variaciones diarias. Para eliminar el efecto del momento del día, ahora queremos suavizar nuestros datos utilizando un filtro de media móvil.
Un filtro de media móvil
En su forma más sencilla, un filtro de media móvil de longitud N toma la media de cada N muestras consecutivas de la forma de onda.
Para aplicar un filtro de media móvil a cada punto de datos, construimos los coeficientes de nuestro filtro para que cada punto tenga el mismo peso y aporte 1/24 a la media total. Esto nos da la temperatura media en cada periodo de 24 horas.
hoursPerDay = 24; coeff24hMA = ones(1, hoursPerDay)/hoursPerDay; avg24hTempC = filter(coeff24hMA, 1, tempC); plot(days,[tempC avg24hTempC]) legend("Hourly Temp","24 Hour Average (delayed)","location","best") ylabel("Temperature (\circC)") xlabel("Time elapsed from Jan 1, 2011 (days)") title("Logan Airport Dry Bulb Temperature (source: NOAA)")

Retardo de filtro
Observe cómo la salida filtrada se retrasa aproximadamente doce horas. Esto se debe al hecho de que nuestro filtro de media móvil presenta un retardo.
Cualquier filtro simétrico de longitud N presentará un retardo de (N-1)/2 muestras. Podemos justificar este retardo manualmente.
fDelay = (length(coeff24hMA)-1)/2; plot(days,tempC, ... days-fDelay/24,avg24hTempC) axis tight legend("Hourly Temp","24 Hour Average","location","best") ylabel("Temperature (\circC)") xlabel("Time elapsed from Jan 1, 2011 (days)") title("Logan Airport Dry Bulb Temperature (source: NOAA)")

Extraer diferencias de media
También podemos utilizar el filtro de media móvil para obtener una mejor estimación de cómo afecta el momento del día a la temperatura general. Para esto, reste primero los datos suavizados de las mediciones de temperatura de cada hora. A continuación, segmente los datos diferenciados en días y tome la media de los 31 días del mes.
figure deltaTempC = tempC - avg24hTempC; deltaTempC = reshape(deltaTempC, 24, 31).'; plot(1:24, mean(deltaTempC)) axis tight title("Mean temperature differential from 24 hour average") xlabel("Hour of day (since midnight)") ylabel("Temperature difference (\circC)")
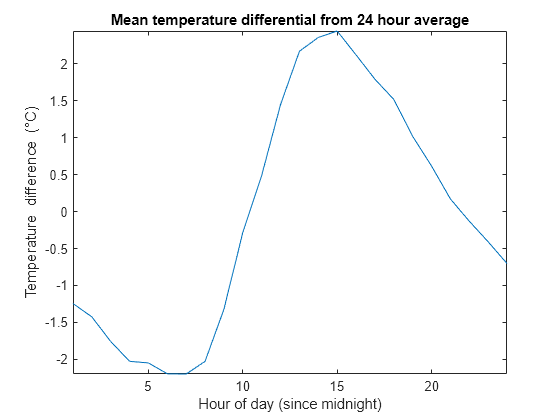
Extraer envolvente pico
En ocasiones, nos gustaría disponer de una estimación que varíe con suavidad de los máximos y mínimos en el cambio diario de la señal de temperatura. Para ello, podemos utilizar la función envelope para conectar máximos y mínimos extremos detectados en un subconjunto del periodo de 24 horas. En este ejemplo, nos aseguramos de que hay al menos 16 horas entre cada máximo y mínimo extremos. También podemos hacernos una idea de las tendencias de los máximos y mínimos tomando la media entre los dos extremos.
[envHigh, envLow] = envelope(tempC,16,"peak"); envMean = (envHigh+envLow)/2; plot(days,tempC, ... days,envHigh, ... days,envMean, ... days,envLow) axis tight legend("Hourly Temp","High","Mean","Low","location","best") ylabel("Temperature (\circC)") xlabel("Time elapsed from Jan 1, 2011 (days)") title("Logan Airport Dry Bulb Temperature (source: NOAA)")

Filtros de media móvil ponderada
Otros tipos de filtros de media móvil no ponderan cada muestra de la misma forma.
Otro filtro común sigue la expansión binomial de . Este tipo de filtro se aproxima a una curva normal para valores grandes de n. Resulta útil para filtrar ruido de alta frecuencia para n pequeños. Para encontrar los coeficientes del filtro binomial, convolucione consigo mismo y, a continuación, convolucione iterativamente la salida con un número estipulado de veces. En este ejemplo, utilice cinco iteraciones totales.
h = [1/2 1/2]; binomialCoeff = conv(h,h); for n = 1:4 binomialCoeff = conv(binomialCoeff,h); end figure fDelay = (length(binomialCoeff)-1)/2; binomialMA = filter(binomialCoeff, 1, tempC); plot(days,tempC, ... days-fDelay/24,binomialMA) axis tight legend("Hourly Temp","Binomial Weighted Average","location","best") ylabel("Temperature (\circC)") xlabel("Time elapsed from Jan 1, 2011 (days)") title("Logan Airport Dry Bulb Temperature (source: NOAA)")
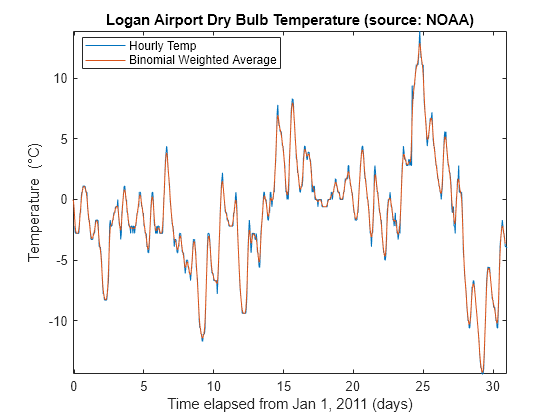
Otro filtro un tanto parecido al filtro de expansión gaussiano es el filtro exponencial de media móvil. Este tipo de filtro de media móvil ponderada es fácil de construir y no requiere un tamaño de ventana grande.
Ajuste un filtro de media móvil ponderada exponencialmente con un parámetro alfa entre cero y uno. Un valor superior de alfa presentará menos suavizado.
alpha = 0.45; exponentialMA = filter(alpha, [1 alpha-1], tempC); plot(days,tempC, ... days-fDelay/24,binomialMA, ... days-1/24,exponentialMA) axis tight legend("Hourly Temp", ... "Binomial Weighted Average", ... "Exponential Weighted Average","location","best") ylabel("Temperature (\circC)") xlabel("Time elapsed from Jan 1, 2011 (days)") title("Logan Airport Dry Bulb Temperature (source: NOAA)")

Amplíe el zoom de las lecturas de un día.
axis([3 4 -5 2])

Filtros de Savitzky-Golay
Observará que, al suavizar los datos, se han recortado un poco los valores extremos.
Para realizar un seguimiento de la señal más de cerca, puede utilizar un filtro de media móvil ponderada que intente ajustar un polinomio de un orden especificado en un número específico de muestras en un sentido de mínimos cuadrados.
Por comodidad, puede utilizar la función sgolayfilt para aplicar un filtro de suavizado de Savitzky-Golay. Para utilizar sgolayfilt, especifique un segmento de longitud impar de los datos y un orden polinomial estrictamente inferior a la longitud del segmento. La función sgolayfilt calcula internamente los coeficientes de polinomios de suavizado, realiza la alineación del retardo y se ocupa de los efectos transitorios al comenzar y finalizar el registro de datos.
cubicMA = sgolayfilt(tempC, 3, 7); quarticMA = sgolayfilt(tempC, 4, 7); quinticMA = sgolayfilt(tempC, 5, 9); plot(days,[tempC cubicMA quarticMA quinticMA]) legend("Hourly Temp","Cubic-Weighted MA", "Quartic-Weighted MA", ... "Quintic-Weighted MA","location","southeast") ylabel("Temperature (\circC)") xlabel("Time elapsed from Jan 1, 2011 (days)") title("Logan Airport Dry Bulb Temperature (source: NOAA)") axis([3 5 -5 2])
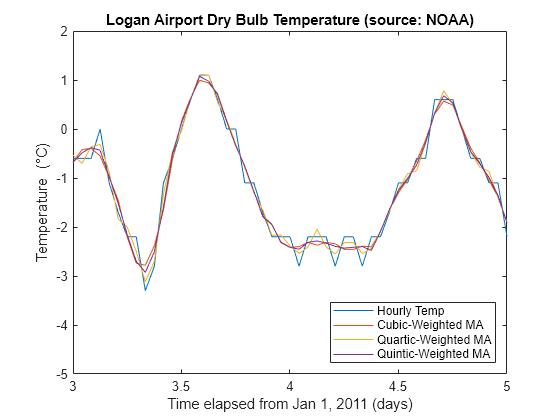
Remuestrear
En ocasiones, conviene remuestrear una señal para aplicar correctamente una media móvil.
En nuestro siguiente ejemplo, muestreamos el voltaje de lazo abierto en la entrada de un instrumento analógico en presencia de interferencias de ruido de un cable de luz de CA de 60 Hz. Muestreamos el voltaje con una tasa de muestreo de 1 kHz.
load openloop60hertz fs = 1000; t = (0:numel(openLoopVoltage)-1) / fs; plot(t,openLoopVoltage) ylabel("Voltage (V)") xlabel("Time (s)") title("Open-loop Voltage Measurement")
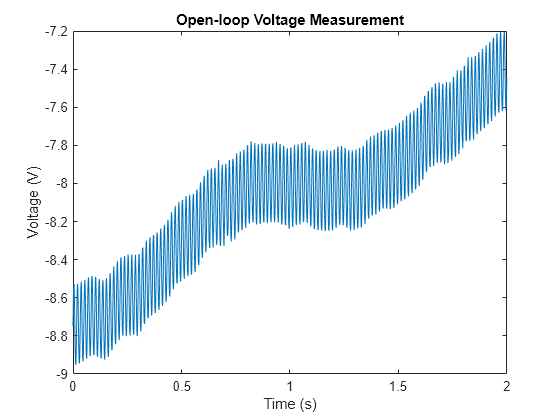
Intentemos eliminar el efecto del ruido del cable utilizando un filtro de media móvil.
Si construye un filtro de media móvil uniformemente ponderada, eliminará todos los componentes periódicos con respecto a la duración del filtro.
Hay aproximadamente 1000 / 60 = 16,667 muestras en un ciclo completo de 60 Hz cuando se muestrea a 1000 Hz. Intentemos "redondear" y utilizar un filtro de 17 puntos. Así, obtendremos un filtrado máximo a una frecuencia fundamental de 1000 Hz / 17 = 58,82 Hz.
plot(t,sgolayfilt(openLoopVoltage,1,17)) ylabel("Voltage (V)") xlabel("Time (s)") title("Open-loop Voltage Measurement") legend("Moving average filter operating at 58.82 Hz", ... "Location","southeast")

Observe cómo, aunque el voltaje se suaviza significativamente, sigue conteniendo una pequeña ondulación de 60 Hz.
Podemos reducir significativamente la ondulación si remuestreamos la señal para capturar un ciclo completo de la señal de 60 Hz con nuestro filtro de media móvil.
Si remuestreamos la señal a 17 * 60 Hz = 1020 Hz, podemos utilizar nuestro filtro de media móvil de 17 puntos para eliminar el ruido del cable de 60 Hz.
fsResamp = 1020; vResamp = resample(openLoopVoltage, fsResamp, fs); tResamp = (0:numel(vResamp)-1) / fsResamp; vAvgResamp = sgolayfilt(vResamp,1,17); plot(tResamp,vAvgResamp) ylabel("Voltage (V)") xlabel("Time (s)") title("Open-loop Voltage Measurement") legend("Moving average filter operating at 60 Hz", ... "Location","southeast")

Filtro de mediana
La media móvil, la media móvil ponderada y los filtros de Savitzky-Golay suavizan todos los datos que filtran. Sin embargo, esto no es siempre lo que se quiere. Por ejemplo, ¿qué hacemos si tomamos nuestros datos de una señal horaria y presentan bordes agudos que no queremos suavizar? Los filtros que hemos tratado hasta ahora no funcionan muy bien:
load clockex yMovingAverage = conv(x,ones(5,1)/5,"same"); ySavitzkyGolay = sgolayfilt(x,3,5); plot(t,x, ... t,yMovingAverage, ... t,ySavitzkyGolay) legend("original signal","moving average","Savitzky-Golay")
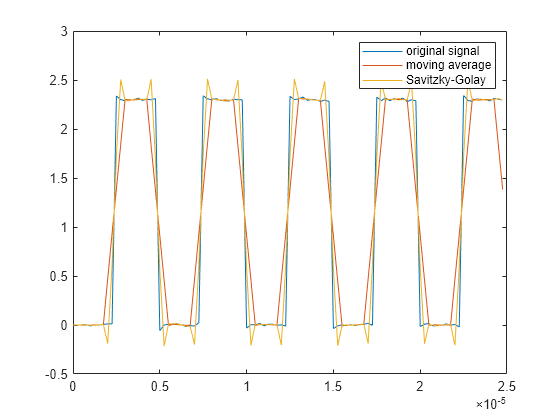
La media móvil y los filtros de Savitzky-Golay infracorrigen y sobrecorrigen cerca de los bordes de la señal horaria.
Una forma sencilla de conservar los bordes y suavizar al mismo tiempo los niveles es utilizar un filtro de mediana:
yMedFilt = medfilt1(x,5,"truncate"); plot(t,x, ... t,yMedFilt) legend("original signal","median filter")

Eliminar valores atípicos con un filtro de Hampel
Muchos filtros son sensibles a los valores atípicos. Un filtro estrechamente relacionado con el filtro de mediana es el filtro de Hampel. Este filtro ayuda a eliminar los valores atípicos de una señal sin suavizar demasiado los datos.
Para verlo, cargue una grabación de audio del silbato de un tren y añada algunos picos de ruido artificiales:
load train
y(1:400:end) = 2.1;
plot(y)
Puesto que cada pico que introducimos presenta una duración de una muestra solo, podemos utilizar un filtro de mediana de solo tres elementos para eliminar los picos.
hold on plot(medfilt1(y,3)) hold off legend("original signal","filtered signal")
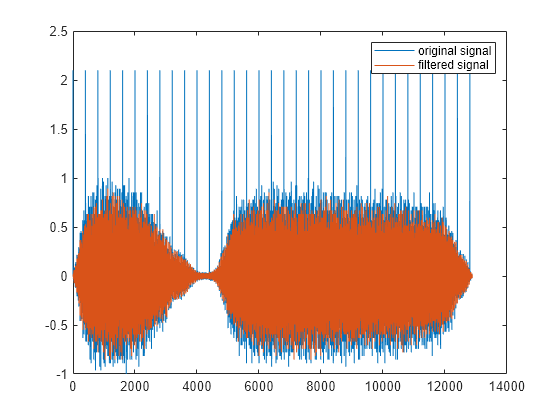
El filtro ha eliminado los picos, pero también un número importante de puntos de datos de la señal original. Un filtro de Hampel presenta un funcionamiento similar a un filtro de mediana. Sin embargo, solo sustituye los valores que son equivalentes a algunas desviaciones estándar del valor local de la mediana.
hampel(y,13) legend("location","best")
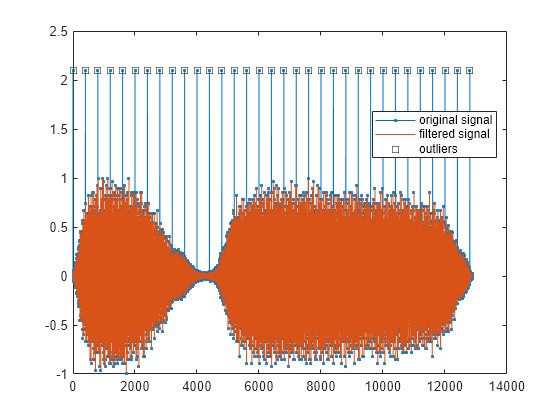
Solo se eliminan los valores atípicos de la señal original.
Más lecturas
Para obtener más información sobre el filtrado y el remuestreo, consulte Signal Processing Toolbox.
Referencia: Kendall, Maurice G., Alan Stuart y J. Keith Ord. The Advanced Theory of Statistics, Vol. 3: Design and Analysis, and Time-Series. 4.ª edición. Londres: Macmillan, 1983.
Consulte también
envelope | hampel | medfilt1 | resample | sgolayfilt