Train Generalized Additive Model for Regression
This example shows how to train a Generalized Additive Model (GAM) for Regression with optimal parameters and how to assess the predictive performance of the trained model. The example first finds the optimal parameter values for a univariate GAM (parameters for linear terms) and then finds the values for a bivariate GAM (parameters for interaction terms). Also, the example explains how to interpret the trained model by examining local effects of terms on a specific prediction and by computing the partial dependence of the predictions on predictors.
Load Sample Data
Load the sample data set NYCHousing2015.
load NYCHousing2015The data set includes 10 variables with information on the sales of properties in New York City in 2015. This example uses these variables to analyze the sale prices (SALEPRICE).
Preprocess the data set. Assume that a SALEPRICE less than or equal to $1000 indicates ownership transfer without a cash consideration. Remove the samples that have this SALEPRICE. Also, remove the outliers identified by the isoutlier function. Then, convert the datetime array (SALEDATE) to the month numbers and move the response variable (SALEPRICE) to the last column. Change zeros in LANDSQUAREFEET, GROSSSQUAREFEET, and YEARBUILT to NaNs.
idx1 = NYCHousing2015.SALEPRICE <= 1000; idx2 = isoutlier(NYCHousing2015.SALEPRICE); NYCHousing2015(idx1|idx2,:) = []; NYCHousing2015.SALEDATE = month(NYCHousing2015.SALEDATE); NYCHousing2015 = movevars(NYCHousing2015,'SALEPRICE','After','SALEDATE'); NYCHousing2015.LANDSQUAREFEET(NYCHousing2015.LANDSQUAREFEET == 0) = NaN; NYCHousing2015.GROSSSQUAREFEET(NYCHousing2015.GROSSSQUAREFEET == 0) = NaN; NYCHousing2015.YEARBUILT(NYCHousing2015.YEARBUILT == 0) = NaN;
Display the first three rows of the table.
head(NYCHousing2015,3)
BOROUGH NEIGHBORHOOD BUILDINGCLASSCATEGORY RESIDENTIALUNITS COMMERCIALUNITS LANDSQUAREFEET GROSSSQUAREFEET YEARBUILT SALEDATE SALEPRICE
_______ ____________ ____________________________ ________________ _______________ ______________ _______________ _________ ________ _________
2 {'BATHGATE'} {'01 ONE FAMILY DWELLINGS'} 1 0 1103 1290 1910 2 3e+05
2 {'BATHGATE'} {'01 ONE FAMILY DWELLINGS'} 1 1 2500 2452 1910 7 4e+05
2 {'BATHGATE'} {'01 ONE FAMILY DWELLINGS'} 1 2 1911 4080 1931 1 5.1e+05
Randomly select 1000 samples by using the datasample function, and partition observations into a training set and a test set by using the cvpartition function. Specify a 10% holdout sample for testing.
rng('default') % For reproducibility NumSamples = 1e3; NYCHousing2015 = datasample(NYCHousing2015,NumSamples,'Replace',false); cv = cvpartition(size(NYCHousing2015,1),'HoldOut',0.10);
Extract the training and test indices, and create tables for training and test data sets.
tbl_training = NYCHousing2015(training(cv),:); tbl_test = NYCHousing2015(test(cv),:);
Train GAM with Optimal Hyperparameters
Train a GAM with hyperparameters that minimize the cross-validation loss by using the OptimizeHyperparameters name-value argument.
You can specify OptimizeHyperparameters as 'auto' or 'all' to find optimal hyperparameter values for both univariate and bivariate parameters. Alternatively, you can find optimal values for univariate parameters using the 'auto-univariate' or 'all-univariate' option, and then find optimal values for bivariate parameters using the 'auto-bivariate' or 'all-bivariate' option. This example uses 'all-univariate' and 'all-bivariate'.
Train a univariate GAM. Specify FitStandardDeviation as true to fit a model for the standard deviation of the response variable as well. A recommended practice is to use optimal hyperparameters when you fit the standard deviation model for the accuracy of the standard deviation estimates. Specify OptimizeHyperparameters as 'all-univariate' so that fitrgam finds optimal values of the InitialLearnRateForPredictors, MaxNumSplitsPerPredictor, and NumTreesPerPredictor name-value arguments. For reproducibility, use the 'expected-improvement-plus' acquisition function. Specify ShowPlots as false and Verbose as 0 to disable plot and message displays, respectively.
Mdl_univariate = fitrgam(tbl_training,'SALEPRICE','FitStandardDeviation',true, ... 'OptimizeHyperparameters','all-univariate', ... 'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName','expected-improvement-plus', ... 'ShowPlots',false,'Verbose',0))
Mdl_univariate =
RegressionGAM
PredictorNames: {'BOROUGH' 'NEIGHBORHOOD' 'BUILDINGCLASSCATEGORY' 'RESIDENTIALUNITS' 'COMMERCIALUNITS' 'LANDSQUAREFEET' 'GROSSSQUAREFEET' 'YEARBUILT' 'SALEDATE'}
ResponseName: 'SALEPRICE'
CategoricalPredictors: [2 3]
ResponseTransform: 'none'
Intercept: 5.1868e+05
IsStandardDeviationFit: 1
NumObservations: 900
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
Properties, Methods
fitrgam returns a RegressionGAM model object that uses the best estimated feasible point. The best estimated feasible point indicates the set of hyperparameters that minimizes the upper confidence bound of the objective function value based on the underlying objective function model of the Bayesian optimization process. You can obtain the best point from the HyperparameterOptimizationResults property or by using the bestPoint function.
x = Mdl_univariate.HyperparameterOptimizationResults.XAtMinEstimatedObjective
x=1×3 table
InitialLearnRateForPredictors MaxNumSplitsPerPredictor NumTreesPerPredictor
_____________________________ ________________________ ____________________
0.063687 1 61
bestPoint(Mdl_univariate.HyperparameterOptimizationResults)
ans=1×3 table
InitialLearnRateForPredictors MaxNumSplitsPerPredictor NumTreesPerPredictor
_____________________________ ________________________ ____________________
0.063687 1 61
For more details on the optimization process, see Optimize GAM Using OptimizeHyperparameters.
Train a bivariate GAM. Specify OptimizeHyperparameters as 'all-bivariate' so that fitrgam finds optimal values of the Interactions, InitialLearnRateForInteractions, MaxNumSplitsPerInteraction, and NumTreesPerInteraction name-value arguments. Use the univariate parameter values in x so that the software finds optimal parameter values for interaction terms based on the x values.
Mdl = fitrgam(tbl_training,'SALEPRICE','FitStandardDeviation',true, ... 'InitialLearnRateForPredictors',x.InitialLearnRateForPredictors, ... 'MaxNumSplitsPerPredictor',x.MaxNumSplitsPerPredictor, ... 'NumTreesPerPredictor',x.NumTreesPerPredictor, ... 'OptimizeHyperparameters','all-bivariate', ... 'HyperparameterOptimizationOptions',struct('AcquisitionFunctionName','expected-improvement-plus', ... 'ShowPlots',false,'Verbose',0))
Mdl =
RegressionGAM
PredictorNames: {'BOROUGH' 'NEIGHBORHOOD' 'BUILDINGCLASSCATEGORY' 'RESIDENTIALUNITS' 'COMMERCIALUNITS' 'LANDSQUAREFEET' 'GROSSSQUAREFEET' 'YEARBUILT' 'SALEDATE'}
ResponseName: 'SALEPRICE'
CategoricalPredictors: [2 3]
ResponseTransform: 'none'
Intercept: 5.1679e+05
Interactions: [3×2 double]
IsStandardDeviationFit: 1
NumObservations: 900
HyperparameterOptimizationResults: [1×1 BayesianOptimization]
Properties, Methods
Display the optimal bivariate hyperparameters.
Mdl.HyperparameterOptimizationResults.XAtMinEstimatedObjective
ans=1×4 table
Interactions InitialLearnRateForInteractions MaxNumSplitsPerInteraction NumTreesPerInteraction
____________ _______________________________ __________________________ ______________________
3 0.0010182 21 302
The model display of Mdl shows a partial list of the model properties. To view the full list of the model properties, double-click the variable name Mdl in the Workspace. The Variables editor opens for Mdl. Alternatively, you can display the properties in the Command Window by using dot notation. For example, display the ReasonForTermination property.
Mdl.ReasonForTermination
ans = struct with fields:
PredictorTrees: 'Terminated after training the requested number of trees.'
InteractionTrees: 'Terminated after training the requested number of trees.'
You can use the ReasonForTermination property to determine whether the trained model contains the specified number of trees for each linear term and each interaction term.
Display the interaction terms in Mdl.
Mdl.Interactions
ans = 3×2
3 6
4 6
5 8
Each row of Interactions represents one interaction term and contains the column indexes of the predictor variables for the interaction term. You can use the Interactions property to check the interaction terms in the model and the order in which fitrgam adds them to the model.
Display the interaction terms in Mdl using the predictor names.
Mdl.PredictorNames(Mdl.Interactions)
ans = 3×2 cell
{'BUILDINGCLASSCATEGORY'} {'LANDSQUAREFEET'}
{'RESIDENTIALUNITS' } {'LANDSQUAREFEET'}
{'COMMERCIALUNITS' } {'YEARBUILT' }
Assess Predictive Performance on New Observations
Assess the performance of the trained model by using the test sample tbl_test and the object functions predict and loss. You can use a full or compact model with these functions.
If you want to assess the performance of the training data set, use the resubstitution object functions: resubPredict and resubLoss. To use these functions, you must use the full model that contains the training data.
Create a compact model to reduce the size of the trained model.
CMdl = compact(Mdl); whos('Mdl','CMdl')
Name Size Bytes Class Attributes CMdl 1x1 11975596 classreg.learning.regr.CompactRegressionGAM Mdl 1x1 12170960 RegressionGAM
Compare the results obtained by including both linear to interaction terms and the results obtained by including only linear terms.
Predict responses and compute mean squared errors for the test data set tbl_test.
[yFit,ySD,yInt] = predict(CMdl,tbl_test); L = loss(CMdl,tbl_test)
L = 1.2746e+11
Find predicted responses and errors without including interaction terms in the trained model.
[yFit_nointeraction,ySD_nointeraction,yInt__nointeraction] = predict(CMdl,tbl_test,'IncludeInteractions',false); L_nointeractions = loss(CMdl,tbl_test,'IncludeInteractions',false)
L_nointeractions = 1.2531e+11
The model achieves a smaller error for the test data set when interaction terms are not included.
Plot the sorted true responses together with the predicted responses and prediction intervals.
yTrue = tbl_test.SALEPRICE; [sortedYTrue,I] = sort(yTrue); figure ax = nexttile; plot(sortedYTrue,'o') hold on plot(yFit(I)) plot(yInt(I,1),'k:') plot(yInt(I,2),'k:') legend('True responses','Predicted responses', ... '95% Prediction interval limits','Location','best') title('Linear and interaction terms') hold off nexttile plot(sortedYTrue,'o') hold on plot(yFit_nointeraction(I)) plot(yInt__nointeraction(I,1),'k:') plot(yInt__nointeraction(I,2),'k:') ylim(ax.YLim) title('Linear terms only') hold off
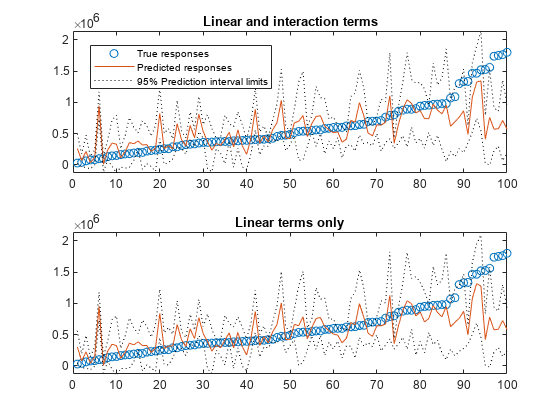
The prediction intervals in the two plots have similar widths.
Interpret Prediction
Interpret the prediction for the first test observation by using the plotLocalEffects function. Also, create partial dependence plots for some important terms in the model by using the plotPartialDependence function.
Predict a response value for the first observation of the test data, and plot the local effects of the terms in CMdl on the prediction. Specify 'IncludeIntercept',true to include the intercept term in the plot.
yFit = predict(CMdl,tbl_test(1,:))
yFit = 5.3526e+05
figure
plotLocalEffects(CMdl,tbl_test(1,:),'IncludeIntercept',true)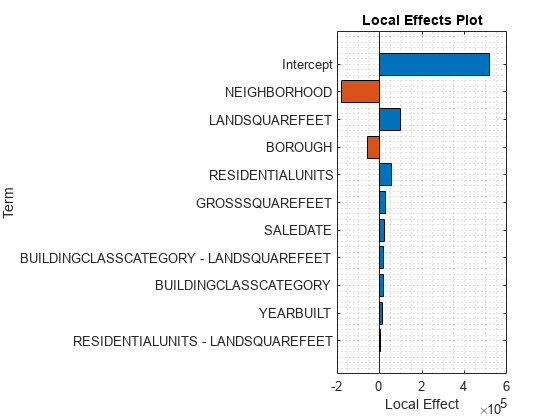
The predict function returns the sale price for the first observation tbl_test(1,:). The plotLocalEffects function creates a horizontal bar graph that shows the local effects of the terms in CMdl on the prediction. Each local effect value shows the contribution of each term to the predicted sale price for tbl_test(1,:).
Compute the partial dependence values for BUILDINGCLASSCATEGORY and plot the sorted values. Specify both the training and test data sets to compute the partial dependence values using both sets.
[pd,x] = partialDependence(CMdl,'BUILDINGCLASSCATEGORY',[tbl_training; tbl_test]); [pd_sorted,I] = sort(pd); x_sorted = x(I); x_sorted = reordercats(x_sorted,I); figure plot(x_sorted,pd_sorted,'o:') xlabel('BUILDINGCLASSCATEGORY') ylabel('SALEPRICE') title('Patial Dependence Plot')
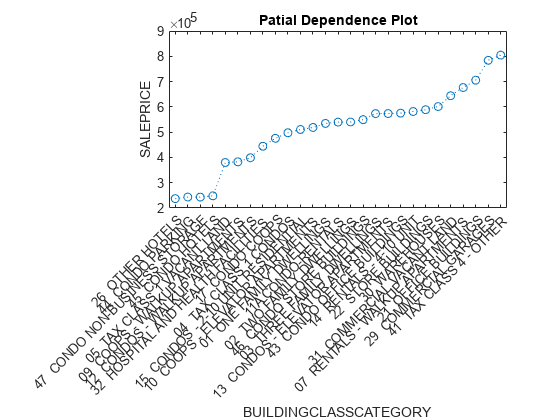
The plotted line represents the averaged partial relationships between the predictor BUILDINGCLASSCATEGORY and the response SALEPRICE in the trained model.
Create a partial dependence plot for the terms RESIDENTIALUNITS and LANDSQUAREFEET using the test data set.
figure plotPartialDependence(CMdl,["RESIDENTIALUNITS","LANDSQUAREFEET"],tbl_test)
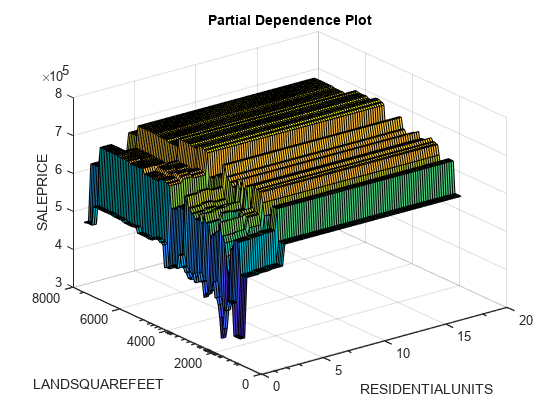
The minor ticks in the x-axis (RESIDENTIALUNITS) and y-axis (LANDSQUAREFEET) represent the unique values of the predictors in the specified data. The predictor values include a few outliers, and most of the RESIDENTIALUNITS and LANDSQUAREFEET values are less than 5 and 5000, respectively. The plot shows that the SALEPRICE values do not vary significantly when the RESIDENTIALUNITS value is greater than 5.
See Also
fitrgam | RegressionGAM | CompactRegressionGAM | plotLocalEffects | plotPartialDependence | bayesopt | optimizableVariable