Problem 3056. Chess probability
The difference in the ratings between two players serves as a predictor of the outcome of a match (the Elo rating system)
If Player A has a rating of Ra and Player B a rating of Rb, the formula for the expected score of Player A is :
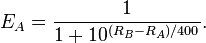
Two players with equal ratings who play against each other are expected to score an equal number of wins. A player whose rating is 100 points greater than their opponent's is expected to score 64%; if the difference is 200 points, then the expected score for the stronger player is 76%.
I give you two ELOs, compute the expected score (round to 3 digits), or probability that the first player wins.
Solution Stats
Problem Comments
Solution Comments
Show commentsProblem Recent Solvers624
Suggested Problems
-
22423 Solvers
-
Project Euler: Problem 5, Smallest multiple
1538 Solvers
-
628 Solvers
-
calculate the length of matrix
2183 Solvers
-
613 Solvers
More from this Author43
Problem Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!