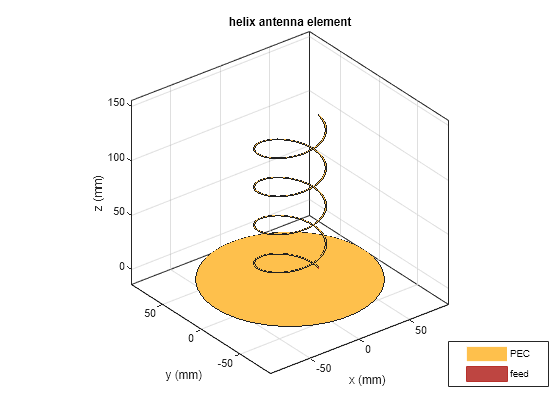
helix
Create helix or conical helix antenna on ground plane
Description
The default helix object creates a helix antenna on a
circular ground plane resonating around 1.56 GHz. You can also create a conical helix
antenna by specifying vector values in the Radius property. The
helix antenna is a common choice in satellite communication.
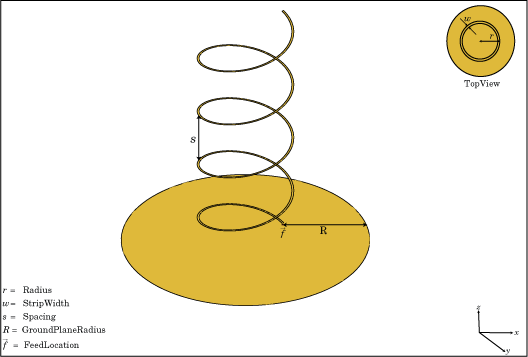
The width of the strip is related to the diameter of an equivalent cylinder by the equation
where:
w is the width of the strip.
d is the diameter of an equivalent cylinder.
r is the radius of an equivalent cylinder.
For a given cylinder radius, use the cylinder2strip utility function to calculate the equivalent width. The
default helix antenna is end-fed. The circular ground plane is on the
xy- plane. Commonly, helix antennas are used in axial mode. In
this mode, the helix circumference is comparable to the operating wavelength and the
helix has maximum directivity along its axis. In normal mode, the helix radius is small
compared to the operating wavelength. In this mode, the helix radiates broadside, that
is, in the plane perpendicular to its axis. The basic equation for the helix is
where
r is the radius of the helix.
θ is the winding angle.
S is the spacing between turns.
For a given pitch angle in degrees, use the helixpitch2spacing utility function to calculate the spacing between the
turns in meters.
Note
In an array of helix antennas, the circular ground plane of the helix is converted to rectangular ground plane.
Creation
Description
ant = helix
ant = helix(PropertyName=Value)PropertyName is the property name
and Value is the corresponding value. You can specify
several name-value arguments in any order as
PropertyName1=Value1,...,PropertyNameN=ValueN.
Properties that you do not specify, retain their default values.
For example, ant = helix(Radius=28e-03) creates a helix
with turns of radius 28e-03 m.
Properties
Object Functions
axialRatio | Calculate and plot axial ratio of antenna or array |
bandwidth | Calculate and plot absolute bandwidth of antenna or array |
beamwidth | Beamwidth of antenna |
charge | Charge distribution on antenna or array surface |
current | Current distribution on antenna or array surface |
design | Create antenna, array, or AI-based antenna resonating at specified frequency |
efficiency | Calculate and plot radiation efficiency of antenna or array |
EHfields | Electric and magnetic fields of antennas or embedded electric and magnetic fields of antenna element in arrays |
feedCurrent | Calculate current at feed for antenna or array |
impedance | Calculate and plot input impedance of antenna or scan impedance of array |
info | Display information about antenna, array, or platform |
memoryEstimate | Estimate memory required to solve antenna or array mesh |
mesh | Generate and view mesh for antennas, arrays, and custom shapes |
meshconfig | Change meshing mode of antenna, array, custom antenna, custom array, or custom geometry |
msiwrite | Write antenna or array analysis data to MSI planet file |
optimize | Optimize antenna and array catalog elements using SADEA or TR-SADEA algorithm |
pattern | Plot radiation pattern of antenna, array, or embedded element of array |
patternAzimuth | Azimuth plane radiation pattern of antenna or array |
patternElevation | Elevation plane radiation pattern of antenna or array |
peakRadiation | Calculate and mark maximum radiation points of antenna or array on radiation pattern |
rcs | Calculate and plot monostatic and bistatic radar cross section (RCS) of platform, antenna, or array |
resonantFrequency | Calculate and plot resonant frequency of antenna |
returnLoss | Calculate and plot return loss of antenna or scan return loss of array |
show | Display antenna, array structures, shapes, or platform |
sparameters | Calculate S-parameters for antenna or array |
stlwrite | Write mesh information to STL file |
vswr | Calculate and plot voltage standing wave ratio (VSWR) of antenna or array element |
Examples
References
[1] Balanis, C.A. Antenna Theory. Analysis and Design, 3rd Ed. New York: Wiley, 2005.
[2] Volakis, John. Antenna Engineering Handbook, 4th Ed. New York: Mcgraw-Hill, 2007.
[3] Zhang, Yan, Q. Ding, J. Chen, S. Lu, Z. Zhu and L. L. Cheng. “A Parametric Study of Helix Antenna for S-Band Satellite Communications.” 9th International Symposium on Antenna Propagation and EM Theory (ISAPE). 2010, pp. 193–196.
[4] Djordjevic, A.R., Zajic, A.G., Ilic, M. M., Stuber, G.L. “Optimization of Helical antennas (Antenna Designer's Notebook)” IEEE Antennas and Propagation Magazine. December, 2006, pp. 107, pp.115.
[5] B. Young, K. A. O'Connor and R. D. Curry, “Reducing the size of helical antennas by means of dielectric loading,” 2011 IEEE Pulsed Power Conference, 2011, pp. 575-579, doi: 10.1109/PPC.2011.6191490
Version History
Introduced in R2015a